人工神经网络简介

      本文主要对人工神经网络基础进行了描述，主要包括人工神经网络的概念、发展、特点、结构、模型。

      本文是个科普文，来自网络资料的整理。

一、人工神经网络的概念

      人工神经网络（Artificial Neural Network，ANN）简称神经网络(NN)，是基于生物学中神经网络的基本原理，在理解和抽象了人脑结构和外界刺激响应机制后，以网络拓扑知识为理论基础，模拟人脑的神经系统对复杂信息的处理机制的一种数学模型。该模型以并行分布的处理能力、高容错性、智能化和自学习等能力为特征，将信息的加工和存储结合在一起，以其独特的知识表示方式和智能化的自适应学习能力，引起各学科领域的关注。它实际上是一个有大量简单元件相互连接而成的复杂网络，具有高度的非线性，能够进行复杂的逻辑操作和非线性关系实现的系统。

      神经网络是一种运算模型，由大量的节点（或称神经元）之间相互联接构成。每个节点代表一种特定的输出函数，称为激活函数（activation function）。每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重（weight），神经网络就是通过这种方式来模拟人类的记忆。网络的输出则取决于网络的结构、网络的连接方式、权重和激活函数。而网络自身通常都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达。神经网络的构筑理念是受到生物的神经网络运作启发而产生的。人工神经网络则是把对生物神经网络的认识与数学统计模型相结合，借助数学统计工具来实现。另一方面在人工智能学的人工感知领域，我们通过数学统计学的方法，使神经网络能够具备类似于人的决定能力和简单的判断能力，这种方法是对传统逻辑学演算的进一步延伸。

      人工神经网络中，神经元处理单元可表示不同的对象，例如特征、字母、概念，或者一些有意义的抽象模式。网络中处理单元的类型分为三类：输入单元、输出单元和隐单元。输入单元接受外部世界的信号与数据；输出单元实现系统处理结果的输出；隐单元是处在输入和输出单元之间，不能由系统外部观察的单元。神经元间的连接权值反映了单元间的连接强度，信息的表示和处理体现在网络处理单元的连接关系中。人工神经网络是一种非程序化、适应性、大脑风格的信息处理，其本质是通过网络的变换和动力学行为得到一种并行分布式的信息处理功能，并在不同程度和层次上模仿人脑神经系统的信息处理功能。

      神经网络，是一种应用类似于大脑神经突触连接结构进行信息处理的数学模型，它是在人类对自身大脑组织结合和思维机制的认识理解基础之上模拟出来的，它是根植于神经科学、数学、思维科学、人工智能、统计学、物理学、计算机科学以及工程科学的一门技术。

二、人工神经网络的发展

      神经网络的发展有悠久的历史。其发展过程大致可以概括为如下4个阶段。

      1. 第一阶段—-启蒙时期

      (1). M-P神经网络模型：20世纪40年代，人们就开始了对神经网络的研究。1943 年，美国心理学家麦克洛奇（Mcculloch）和数学家皮兹（Pitts）提出了M-P模型，此模型比较简单，但是意义重大。在模型中，通过把神经元看作个功能逻辑器件来实现算法，从此开创了神经网络模型的理论研究。

      (2). Hebb规则：1949 年，心理学家赫布（Hebb）出版了《The Organization of Behavior》（行为组织学），他在书中提出了突触连接强度可变的假设。这个假设认为学习过程最终发生在神经元之间的突触部位，突触的连接强度随之突触前后神经元的活动而变化。这一假设发展成为后来神经网络中非常著名的Hebb规则。这一法则告诉人们，神经元之间突触的联系强度是可变的，这种可变性是学习和记忆的基础。Hebb法则为构造有学习功能的神经网络模型奠定了基础。

      (3). 感知器模型：1957 年，罗森勃拉特（Rosenblatt）以M-P 模型为基础，提出了感知器（Perceptron）模型。感知器模型具有现代神经网络的基本原则，并且它的结构非常符合神经生理学。这是一个具有连续可调权值矢量的MP神经网络模型，经过训练可以达到对一定的输入矢量模式进行分类和识别的目的，它虽然比较简单，却是第一个真正意义上的神经网络。Rosenblatt 证明了两层感知器能够对输入进行分类，他还提出了带隐层处理元件的三层感知器这一重要的研究方向。Rosenblatt 的神经网络模型包含了一些现代神经计算机的基本原理，从而形成神经网络方法和技术的重大突破。

      (4). ADALINE网络模型： 1959年，美国著名工程师威德罗（B.Widrow）和霍夫（M.Hoff）等人提出了自适应线性元件(Adaptive linear element，简称Adaline)和Widrow-Hoff学习规则（又称最小均方差算法或称δ规则）的神经网络训练方法，并将其应用于实际工程，成为第一个用于解决实际问题的人工神经网络，促进了神经网络的研究应用和发展。ADALINE网络模型是一种连续取值的自适应线性神经元网络模型，可以用于自适应系统。

      2. 第二阶段—-低潮时期

      人工智能的创始人之一Minsky和Papert对以感知器为代表的网络系统的功能及局限性从数学上做了深入研究，于1969年发表了轰动一时《Perceptrons》一书，指出简单的线性感知器的功能是有限的，它无法解决线性不可分的两类样本的分类问题，如简单的线性感知器不可能实现“异或”的逻辑关系等。这一论断给当时人工神经元网络的研究带来沉重的打击。开始了神经网络发展史上长达10年的低潮期。

      (1). 自组织神经网络SOM模型：1972年，芬兰的KohonenT.教授，提出了自组织神经网络SOM(Self-Organizing feature map)。后来的神经网络主要是根据KohonenT.的工作来实现的。SOM网络是一类无导师学习网络，主要用于模式识别﹑语音识别及分类问题。它采用一种“胜者为王”的竞争学习算法，与先前提出的感知器有很大的不同，同时它的学习训练方式是无指导训练，是一种自组织网络。这种学习训练方式往往是在不知道有哪些分类类型存在时，用作提取分类信息的一种训练。

      (2). 自适应共振理论ART：1976年，美国Grossberg教授提出了著名的自适应共振理论ART(Adaptive Resonance Theory)，其学习过程具有自组织和自稳定的特征。

      3. 第三阶段—-复兴时期

      (1). Hopfield模型：1982年，美国物理学家霍普菲尔德（Hopfield）提出了一种离散神经网络，即离散Hopfield网络，从而有力地推动了神经网络的研究。在网络中，它首次将李雅普诺夫（Lyapunov）函数引入其中，后来的研究学者也将Lyapunov函数称为能量函数。证明了网络的稳定性。1984年，Hopfield 又提出了一种连续神经网络，将网络中神经元的激活函数由离散型改为连续型。1985 年，Hopfield和Tank利用Hopfield神经网络解决了著名的旅行推销商问题（Travelling Salesman Problem）。Hopfield神经网络是一组非线性微分方程。Hopfield的模型不仅对人工神经网络信息存储和提取功能进行了非线性数学概括，提出了动力方程和学习方程，还对网络算法提供了重要公式和参数，使人工神经网络的构造和学习有了理论指导，在Hopfield模型的影响下，大量学者又激发起研究神经网络的热情，积极投身于这一学术领域中。因为Hopfield 神经网络在众多方面具有巨大潜力，所以人们对神经网络的研究十分地重视，更多的人开始了研究神经网络，极大地推动了神经网络的发展。

      (2). Boltzmann机模型：1983年，Kirkpatrick等人认识到模拟退火算法可用于NP完全组合优化问题的求解，这种模拟高温物体退火过程来找寻全局最优解的方法最早由Metropli等人1953年提出的。1984年，Hinton与年轻学者Sejnowski等合作提出了大规模并行网络学习机，并明确提出隐单元的概念，这种学习机后来被称为Boltzmann机。

      Hinton和Sejnowsky利用统计物理学的感念和方法，首次提出的多层网络的学习算法，称为Boltzmann 机模型。

      (3). BP神经网络模型：1986年，儒默哈特（D.E.Ru melhart）等人在多层神经网络模型的基础上，提出了多层神经网络权值修正的反向传播学习算法—-BP算法（Error Back-Propagation），解决了多层前向神经网络的学习问题，证明了多层神经网络具有很强的学习能力，它可以完成许多学习任务，解决许多实际问题。

      (4). 并行分布处理理论：1986年，由Rumelhart和McCkekkand主编的《Parallel Distributed Processing：Exploration in the Microstructures of Cognition》，该书中，他们建立了并行分布处理理论，主要致力于认知的微观研究，同时对具有非线性连续转移函数的多层前馈网络的误差反向传播算法即BP算法进行了详尽的分析，解决了长期以来没有权值调整有效算法的难题。可以求解感知机所不能解决的问题，回答了《Perceptrons》一书中关于神经网络局限性的问题，从实践上证实了人工神经网络有很强的运算能力。

      (5). 细胞神经网络模型：1988年，Chua和Yang提出了细胞神经网络（CNN）模型，它是一个细胞自动机特性的大规模非线性计算机仿真系统。Kosko建立了双向联想存储模型（BAM），它具有非监督学习能力。

      (6). Darwinism模型：Edelman提出的Darwinism模型在90年代初产生了很大的影响，他建立了一种神经网络系统理论。

      (7). 1988年，Linsker对感知机网络提出了新的自组织理论，并在Shanon信息论的基础上形成了最大互信息理论，从而点燃了基于NN的信息应用理论的光芒。

      (8). 1988年，Broomhead和Lowe用径向基函数(Radialbasis function, RBF)提出分层网络的设计方法，从而将NN的设计与数值分析和线性适应滤波相挂钩。

      (9). 1991年，Haken把协同引入神经网络，在他的理论框架中，他认为，认知过程是自发的，并断言模式识别过程即是模式形成过程。

      (10). 1994年，廖晓昕关于细胞神经网络的数学理论与基础的提出，带来了这个领域新的进展。通过拓广神经网络的激活函数类，给出了更一般的时滞细胞神经网络(DCNN)、Hopfield神经网络（HNN）、双向联想记忆网络（BAM）模型。

      (11). 90年代初，Vapnik等提出了支持向量机(Supportvector machines, SVM)和VC(Vapnik-Chervonenkis)维数的概念。

      经过多年的发展，已有上百种的神经网络模型被提出。

      4. 第四阶段—-高潮时期[注：自己分的，不准确 ^_^ 

      深度学习(Deep Learning,DL)由Hinton等人于2006年提出，是机器学习(Machine Learning, ML)的一个新领域。深度学习本质上是构建含有多隐层的机器学习架构模型，通过大规模数据进行训练，得到大量更具代表性的特征信息。深度学习算法打破了传统神经网络对层数的限制，可根据设计者需要选择网络层数。

      关于深度学习的文章可以参考：深度学习概述_网络资源是无限的-CSDN博客_深度学习概述

三、人工神经网络的特点

      神经网络是由存储在网络内部的大量神经元通过节点连接权组成的一种信息响应网状拓扑结构，它采用了并行分布式的信号处理机制，因而具有较快的处理速度和较强的容错能力。

      1. 神经网络模型用于模拟人脑神经元的活动过程，其中包括对信息的加工、处理、存储、和搜索等过程。人工神经网络具有如下基本特点：

      (1). 高度的并行性：人工神经网络有许多相同的简单处理单元并联组合而成，虽然每一个神经元的功能简单，但大量简单神经元并行处理能力和效果，却十分惊人。人工神经网络和人类的大脑类似，不但结构上是并行的，它的处理顺序也是并行和同时的。在同一层内的处理单元都是同时操作的，即神经网络的计算功能分布在多个处理单元上，而一般计算机通常有一个处理单元，其处理顺序是串行的。

      人脑神经元之间传递脉冲信号的速度远低于冯·诺依曼计算机的工作速度，前者为毫秒量级，后者的时钟频率通常可达108Hz 或更高的速率。但是，由于人脑是一个大规模并行与串行组合处理系统，因而在许多问题上可以做出快速判断、决策和处理，其速度可以远高于串行结构的冯·诺依曼计算机。人工神经网络的基本结构模仿人脑，具有并行处理的特征，可以大大提高工作速度。

      (2). 高度的非线性全局作用：人工神经网络每个神经元接受大量其他神经元的输入，并通过并行网络产生输出，影响其他神经元，网络之间的这种互相制约和互相影响，实现了从输入状态到输出状态空间的非线性映射，从全局的观点来看，网络整体性能不是网络局部性能的叠加，而表现出某种集体性的行为。

      非线性关系是自然界的普遍特性。大脑的智慧就是一种非线性现象。人工神经元处于激活或抑制二种不同的状态，这种行为在数学上表现为一种非线性人工神经网络。具有阈值的神经元构成的网络具有更好的性能，可以提高容错性和存储容量。

      (3). 联想记忆功能和良好的容错性：人工神经网络通过自身的特有网络结构将处理的数据信息存储在神经元之间的权值中，具有联想记忆功能，从单一的某个权值并看不出其所记忆的信息内容，因而是分布式的存储形式，这就使得网络有很好的容错性，并可以进行特征提取、缺损模式复原、聚类分析等模式信息处理工作，又可以作模式联想、分类、识别工作。它可以从不完善的数据和图形中进行学习并做出决定。由于知识存在于整个系统中，而不只是一个存储单元中，预订比例的结点不参与运算，对整个系统的性能不会产生重大的影响。能够处理那些有噪声或不完全的数据，具有泛化功能和很强的容错能力。

      一个神经网络通常由多个神经元广泛连接而成。一个系统的整体行为不仅取决于单个神经元的特征，而且可能主要由单元之间的相互作用、相互连接所决定。通过单元之间的大量连接模拟大脑的非局限性。联想记忆是非局限性的典型例子。

      (4). 良好的自适应、自学习功能：人工神经网络通过学习训练获得网络的权值与结构，呈现出很强的自学习能力和对环境的自适应能力。神经网络所具有的自学习过程模拟了人的形象思维方法，这是与传统符号逻辑完全不同的一种非逻辑非语言。自适应性根据所提供的数据，通过学习和训练，找出输入和输出之间的内在关系，从而求取问题的解，而不是依据对问题的经验知识和规则，因而具有自适应功能，这对于弱化权重确定人为因素是十分有益的。

      (5). 知识的分布存储：在神经网络中，知识不是存储在特定的存储单元中，而是分布在整个系统中，要存储多个知识就需要很多链接。在计算机中，只要给定一个地址就可得到一个或一组数据。在神经网络中要获得存储的知识则采用“联想”的办法，这类似人类和动物的联想记忆。人类善于根据联想正确识别图形，人工神经网络也是这样。神经网络采用分布式存储方式表示知识，通过网络对输入信息的响应将激活信号分布在网络神经元上，通过网络训练和学习使得特征被准确地记忆在网络的连接权值上，当同样的模式再次输入时网络就可以进行快速判断。

      (6). 非凸性：一个系统的演化方向，在一定条件下将取决于某个特定的状态函数。例如能量函数，它的极值相应于系统比较稳定的状态。非凸性是指这种函数有多个极值，故系统具有多个较稳定的平衡态，这将导致系统演化的多样性。

      正是神经网络所具有的这种学习和适应能力、自组织、非线性和运算高度并行的能力，解决了传统人工智能对于直觉处理方面的缺陷，例如对非结构化信息、语音模式识别等的处理，使之成功应用于神经专家系统、组合优化、智能控制、预测、模式识别等领域。

      2. 人工神经网络是一种旨在模仿人脑结构及其功能的信息处理系统。因此，它在功能上具有某些智能特点：

      (1). 联想记忆功能：由于神经网络具有分布存储信息和并行计算的性能，因此它具有对外界刺激和输入信息进行联想记忆的能力。这种能力是通过神经元之间的协同结构及信息处理的集体行为而实现的。神经网络通过预先存储信息和学习机制进行自适应训练，可以从不完整的信息和噪声干扰中恢复原始的完整的信息。这一功能使神经网络在图像复原﹑语音处理﹑模式识别与分类方面具有重要的应用前景。联想记忆又分自联想记忆和异联想记忆两种。

      (2). 分类与识别功能：神经网络对外界输入样本有很强的识别与分类能力。对输入样本的分类实际上是在样本空间找出符合分类要求的分割区域，每个区域内的样本属于一类。

      (3). 优化计算功能：优化计算是指在已知的约束条件下，寻找一组参数组合，使该组合确定的目标函数达到最小。将优化约束信息（与目标函数有关）存储于神经网络的连接权矩阵之中，神经网络的工作状态以动态系统方程式描述。设置一组随机数据作为起始条件，当系统的状态趋于稳定时，神经网络方程的解作为输出优化结果。优化计算在TSP及生产调度问题上有重要应用。

      (4). 非线性映射功能：在许多实际问题中，如过程控制﹑系统辨识﹑故障诊断﹑机器人控制等诸多领域，系统的输入与输出之间存在复杂的非线性关系，对于这类系统，往往难以用传统的数理方程建立其数学模型。神经网络在这方面有独到的优势，设计合理的神经网络通过对系统输入输出样本进行训练学习，从理论上讲，能够以任意精度逼近任意复杂的非线性函数。神经网络的这一优良性能使其可以作为多维非线性函数的通用数学模型。

四、人工神经网络的结构

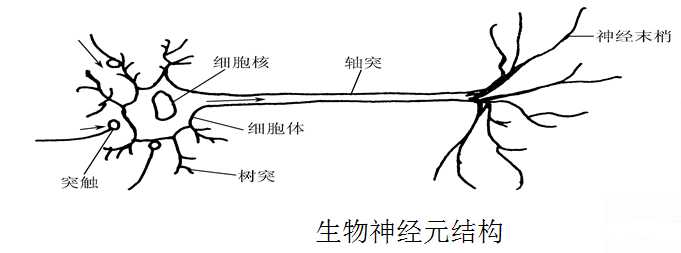
      1. 生物神经元的结构：神经细胞是构成神经系统的基本单元，称之为生物神经元，简称神经元。神经元主要由三部分构成：（1）细胞体;（2）轴突;（3）树突。如下图所示：

      突触是神经元之间相互连接的接口部分，即一个神经元的神经末梢与另一个神经元的树突相接触的交界面，位于神经元的神经末梢尾端。突触是轴突的终端。

      大脑可视作为1000多亿神经元组成的神经网络。神经元的信息传递和处理是一种电化学活动．树突由于电化学作用接受外界的刺激，通过胞体内的活动体现为轴突电位，当轴突电位达到一定的值则形成神经脉冲或动作电位；再通过轴突末梢传递给其它的神经元．从控制论的观点来看；这一过程可以看作一个多输入单输出非线性系统的动态过程。

      神经元的功能特性：（1）时空整合功能；（2）神经元的动态极化性；（3）兴奋与抑制状态；（4）结构的可塑性；（5）脉冲与电位信号的转换；（6）突触延期和不应期；（7）学习、遗忘和疲劳。

      2.  人工神经元结构：人工神经元的研究源于脑神经元学说，19世纪末，在生物、生理学领域，Waldeger等人创建了神经元学说。

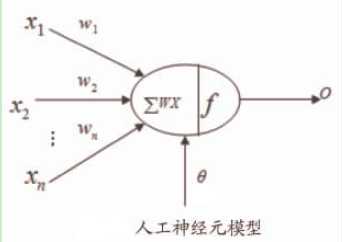
      人工神经网络是由大量处理单元经广泛互连而组成的人工网络，用来模拟脑神经系统的结构和功能。而这些处理单元我们把它称作人工神经元。人工神经网络可看成是以人工神经元为节点，用有向加权弧连接起来的有向图。在此有向图中，人工神经元就是对生物神经元的模拟，而有向弧则是轴突—-突触—-树突对的模拟。有向弧的权值表示相互连接的两个人工神经元间相互作用的强弱。人工神经元结构如下图所示：

      神经网络从两个方面模拟大脑：

      (1). 神经网络获取的知识是从外界环境中学习得来的。

      (2). 内部神经元的连接强度，即突触权值，用于储存获取的知识。

      神经网络系统由能够处理人类大脑不同部分之间信息传递的由大量神经元连接形成的拓扑结构组成，依赖于这些庞大的神经元数目和它们之间的联系，人类的大脑能够收到输入的信息的刺激由分布式并行处理的神经元相互连接进行非线性映射处理，从而实现复杂的信息处理和推理任务。

      对于某个处理单元（神经元）来说，假设来自其他处理单元（神经元）i的信息为Xi，它们与本处理单元的互相作用强度即连接权值为Wi, i=0,1,…,n-1,处理单元的内部阈值为θ。

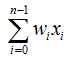
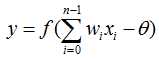
那么本处理单元（神经元）的输入为：，而处理单元的输出为：.

式中，xi为第i个元素的输入，wi为第i个处理单元与本处理单元的互联权重即神经元连接权值。f称为激活函数或作用函数，它决定节点（神经元）的输出。θ表示隐含层神经节点的阈值。

      神经网络的主要工作是建立模型和确定权值，一般有前向型和反馈型两种网络结构。通常神经网络的学习和训练需要一组输入数据和输出数据对，选择网络模型和传递、训练函数后，神经网络计算得到输出结果，根据实际输出和期望输出之间的误差进行权值的修正，在网络进行判断的时候就只有输入数据而没有预期的输出结果。神经网络一个相当重要的能力是其网络能通过它的神经元权值和阈值的不断调整从环境中进行学习，直到网络的输出误差达到预期的结果，就认为网络训练结束。

      对于这样一种多输入、单输出的基本单元可以进一步从生物化学、电生物学、数学等方面给出描述其功能的模型。利用大量神经元相互连接组成的人工神经网络，将显示出人脑的若干特征，人工神经网络也具有初步的自适应与自组织能力。在学习或训练过程中改变突触权重wij值，以适应周围环境的要求。同一网络因学习方式及内容不同可具有不同的功能。人工神经网络是一个具有学习能力的系统，可以发展知识，以至超过设计者原有的知识水平。通常，它的学习(或训练)方式可分为两种，一种是有监督(supervised)或称有导师的学习，这时利用给定的样本标准进行分类或模仿；另一种是无监督(unsupervised)学习或称无导师学习，这时，只规定学习方式或某些规则，而具体的学习内容随系统所处环境(即输入信号情况)而异，系统可以自动发现环境特征和规律性，具有更近似于人脑的功能。

      在人工神经网络设计及应用研究中，通常需要考虑三个方面的内容，即神经元激活函数、神经元之间的连接形式和网络的学习(训练)。

      3. 神经网络的学习形式：在构造神经网络时，其神经元的传递函数和转换函数就已经确定了。在网络的学习过程中是无法改变转换函数的，因此如果想要改变网络输出的大小，只能通过改变加权求和的输入来达到。由于神经元只能对网络的输入信号进行响应处理，想要改变网络的加权输入只能修改网络神经元的权参数，因此神经网络的学习就是改变权值矩阵的过程。

      4. 神经网络的工作过程：神经网络的工作过程包括离线学习和在线判断两部分。学习过程中各神经元进行规则学习，权参数调整，进行非线性映射关系拟合以达到训练精度；判断阶段则是训练好的稳定的网络读取输入信息通过计算得到输出结果。

      5. 神经网络的学习规则：神经网络的学习规则是修正权值的一种算法，分为联想式和非联想式学习，有监督学习和无监督学习等。下面介绍几个常用的学习规则。

      (1). 误差修正型规则：是一种有监督的学习方法，根据实际输出和期望输出的误差进行网络连接权值的修正，最终网络误差小于目标函数达到预期结果。

      误差修正法，权值的调整与网络的输出误差有关， 它包括δ学习规则、Widrow-Hoff学习规则、感知器学习规则和误差反向传播的BP(Back Propagation)学习规则等。

      (2). 竞争型规则：无监督学习过程，网络仅根据提供的一些学习样本进行自组织学习，没有期望输出，通过神经元相互竞争对外界刺激模式响应的权利进行网络权值的调整来适应输入的样本数据。

      对于无监督学习的情况，事先不给定标准样本，直接将网络置于“环境”之中，学习(训练)阶段与应用(工作)阶段成为一体。

      (3). Hebb型规则：利用神经元之间的活化值(激活值)来反映它们之间联接性的变化，即根据相互连接的神经元之间的活化值(激活值)来修正其权值。

      在Hebb学习规则中，学习信号简单地等于神经元的输出。Hebb学习规则代表一种纯前馈﹑无导师学习。该学习规则至今在各种神经网络模型中起着重要作用。典型的应用如利用Hebb规则训练线性联想器的权矩阵。

      (4). 随机型规则：在学习过程中结合了随机、概率论和能量函数的思想，根据目标函数（即网络输出均方差）的变化调整网络的参数，最终使网络目标函数达到收敛值。

      6. 激活函数：在神经网络中，网络解决问题的能力与效率除了与网络结构有关外，在很大程度上取决于网络所采用的激活函数。激活函数的选择对网络的收敛速度有较大的影响，针对不同的实际问题，激活函数的选择也应不同。

      神经元在输入信号作用下产生输出信号的规律由神经元功能函数f（Activation Function）给出，也称激活函数，或称转移函数，这是神经元模型的外特性。它包含了从输入信号到净输入、再到激活值、最终产生输出信号的过程。综合了净输入、f函数的作用。f函数形式多样，利用它们的不同特性可以构成功能各异的神经网络。

      常用的激活函数有以下几种形式：

      (1). 阈值函数：该函数通常也称为阶跃函数。当激活函数采用阶跃函数时，人工神经元模型即为MP模型。此时神经元的输出取１或０，反应了神经元的兴奋或抑制。

      (2). 线性函数：该函数可以在输出结果为任意值时作为输出神经元的激活函数，但是当网络复杂时，线性激活函数大大降低网络的收敛性，故一般较少采用。

      (3). 对数S形函数：对数S形函数的输出介于0~1之间，常被要求为输出在０～１范围的信号选用。它是神经元中使用最为广泛的激活函数。

      (4). 双曲正切S形函数：双曲正切S形函数类似于被平滑的阶跃函数，形状与对数S形函数相同，以原点对称，其输出介于-１~１之间，常常被要求为输出在-１~１范围的信号选用。

      7. 神经元之间的连接形式：神经网络是一个复杂的互连系统，单元之间的互连模式将对网络的性质和功能产生重要影响。互连模式种类繁多。

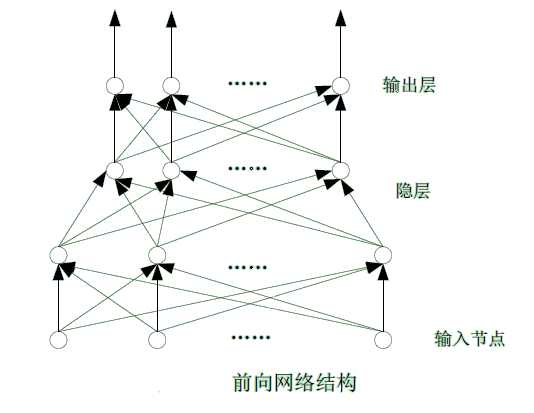
      (1). 前向网络(前馈网络)：网络可以分为若干“层”，各层按信号传输先后顺序依次排列，第i层的神经元只接受第(i-1)层神经元给出的信号，各神经元之间没有反馈。前馈型网络可用一有向无环路图表示，如下图所示：

      可以看出，输入节点并无计算功能，只是为了表征输入矢量各元素值。各层节点表示具有计算功能的神经元，称为计算单元。每个计算单元可以有任意个输入，但只有一个输出，它可送到多个节点作输入。称输入节点层为第零层。计算单元的各节点层从下至上依次称为第1至第N层，由此构成N层前向网络。(也有把输入节点层称为第1层，于是对N层网络将变为N+1个节点层序号。)

      第一节点层与输出节点统称为“可见层”，而其他中间层则称为隐含层(hidden layer)，这些神经元称为隐节点。BP网络就是典型的前向网络。

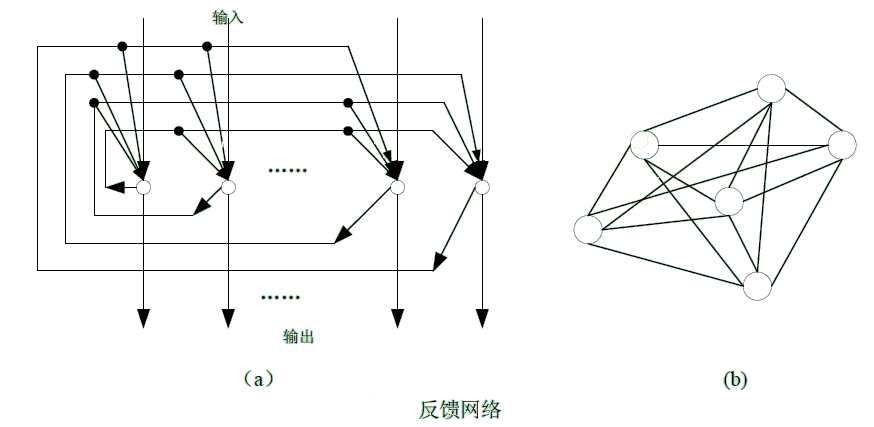
      (2). 反馈网络：典型的反馈型神经网络如下图a所示：

      每个节点都表示一个计算单元，同时接受外加输入和其它各节点的反馈输入，每个节点也都直接向外部输出。Hopfield网络即属此种类型。在某些反馈网络中，各神经元除接受外加输入与其它各节点反馈输入之外，还包括自身反馈。有时，反馈型神经网络也可表示为一张完全的无向图，如上图b。图中，每一个连接都是双向的。这里，第i个神经元对于第j个神经元的反馈与第j至i神经元反馈之突触权重相等，也即wij=wji。

      以上介绍了两种最基本的人工神经网络结构，实际上，人工神经网络还有许多种连接形式，例如，从输出层到输入层有反馈的前向网络，同层内或异层间有相互反馈的多层网络等等。

五、人工神经网络模型

      1. 人工神经网络的分类：

      按性能分：连续型和离散型网络，或确定型和随机型网络。

      按拓扑结构分：前向网络和反馈网络。

      前向网络有自适应线性神经网络(AdaptiveLinear，简称Adaline)、单层感知器、多层感知器、BP等。

      前向网络，网络中各个神经元接受前一级的输入，并输出到下一级，网络中没有反馈，可以用一个有向无环路图表示。这种网络实现信号从输入空间到输出空间的变换，它的信息处理能力来自于简单非线性函数的多次复合。网络结构简单，易于实现。反传网络是一种典型的前向网络。

      反馈网络有Hopfield、Hamming、BAM等。

      反馈网络，网络内神经元间有反馈，可以用一个无向的完备图表示。这种神经网络的信息处理是状态的变换，可以用动力学系统理论处理。系统的稳定性与联想记忆功能有密切关系。Hopfield网络、波耳兹曼机均属于这种类型。

      按学习方法分：有教师(监督)的学习网络和无教师(监督)的学习网络。

      按连接突触性质分：一阶线性关联网络和高阶非线性关联网络。

      2. 生物神经元模型：人脑是自然界所造就的高级动物，人的思维是由人脑来完成的，而思维则是人类智能的集中体现。人脑的皮层中包含100亿个神经元、60万亿个神经突触，以及他们的连接体。神经系统的基本结构和功能单位就是神经细胞，即神经元，它主要由细胞体、树突、轴突和突触组成。人类的神经元具备以下几个基本功能特性：时空整合功能；神经元的动态极化性；兴奋与抑制状态；结构的可塑性；脉冲与电位信号的转换；突触延期和不延期；学习、遗忘和疲劳；神经网络是由大量的神经元单元相互连接而构成的网络系统。

      3. 人工神经网络模型：人工神经网络，使通过模仿生物神经网络的行为特征，进行分布式并行信息处理的数学模型。这种网络依靠系统的复杂度，通过调整内部大量节点之间相互连接的关系，从而达到信息处理的目的。人工神经网络具有自学习和自适应的能力，可以通过预先提供的一批相互对应的输入输出数据，分析两者的内在关系和规律，最终通过这些规律形成一个复杂的非线性系统函数，这种学习分析过程被称作“训练”。神经元的每一个输入连接都有突触连接强度，用一个连接权值来表示，即将产生的信号通过连接强度放大，每一个输入量都对应有一个相关联的权重。处理单元将经过权重的输入量化，然后相加求得加权值之和，计算出输出量，这个输出量是权重和的函数，一般称此函数为传递函数。

      4. 感知器模型：

      感知器模型是美国学者罗森勃拉特（Rosenblatt）为研究大脑的存储、学习和认知过程而提出的一类具有自学习能力的神经网络模型，它把神经网络的研究从纯理论探讨引向了从工程上的实现。

      Rosenblatt提出的感知器模型是一个只有单层计算单元的前向神经网络，称为单层感知器。

      单层感知器模型的学习算法，算法思想：首先把连接权和阈值初始化为较小的非零随机数，然后把有n个连接权值的输入送入网络，经加权运算处理，得到的输出如果与所期望的输出有较大的差别，就对连接权值参数按照某种算法进行自动调整，经过多次反复，直到所得到的输出与所期望的输出间的差别满足要求为止。

      线性不可分问题：单层感知器不能表达的问题被称为线性不可分问题。 1969年，明斯基证明了“异或”问题是线性不可分问题。

      线性不可分函数的数量随着输入变量个数的增加而快速增加，甚至远远超过了线性可分函数的个数。也就是说，单层感知器不能表达的问题的数量远远超过了它所能表达的问题的数量。

      多层感知器：在单层感知器的输入部分和输出层之间加入一层或多层处理单元，就构成了二层或多层感知器。

      在多层感知器模型中，只允许某一层的连接权值可调，这是因为无法知道网络隐层的神经元的理想输出，因而难以给出一个有效的多层感知器学习算法。

      多层感知器克服了单层感知器的许多缺点，原来一些单层感知器无法解决的问题，在多层感知器中就可以解决。例如，应用二层感知器就可以解决异或逻辑运算问题

      5. 反向传播模型：

      反向传播模型也称B-P模型，是一种用于前向多层的反向传播学习算法。之所以称它是一种学习方法，是因为用它可以对组成前向多层网络的各人工神经元之间的连接权值进行不断的修改，从而使该前向多层网络能够将输入它的信息变换成所期望的输出信息。之所以将其称作为反向学习算法，是因为在修改各人工神经元的连接权值时，所依据的是该网络的实际输出与其期望的输出之差，将这一差值反向一层一层的向回传播，来决定连接权值的修改。

      B-P算法的网络结构是一个前向多层网络。它是在1986年，由Rumelhant和Mcllelland提出的。是一种多层网络的“逆推”学习算法。其基本思想是，学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时，输入样本从输入层传入，经隐层逐层处理后，传向输出层。若输出层的实际输出与期望输出不符，则转向误差的反向传播阶段。误差的反向传播是将输出误差以某种形式通过隐层向输入层逐层反传，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，此误差信号即作为修正各单元权值的依据。这种信号正向传播与误差反向传播的各层权值调整过程，是周而复始地进行。权值不断调整过程，也就是网络的学习训练过程。此过程一直进行到网络输出的误差减少到可以接受的程度，或进行到预先设定的学习次数为止。

      反向传播网络的学习算法：B-P算法的学习目的是对网络的连接权值进行调整，使得调整后的网络对任一输入都能得到所期望的输出。

      学习过程由正向传播和反向传播组成。

      正向传播用于对前向网络进行计算，即对某一输入信息，经过网络计算后求出它的输出结果。

      反向传播用于逐层传递误差，修改神经元间的连接权值，以使网络对输入信息经过计算后所得到的输出能达到期望的误差要求。

      B-P算法的学习过程如下：

      (1). 选择一组训练样例，每一个样例由输入信息和期望的输出结果两部分组成。

      (2). 从训练样例集中取一样例，把输入信息输入到网络中。

      (3). 分别计算经神经元处理后的各层节点的输出。

      (4). 计算网络的实际输出和期望输出的误差。

      (5). 从输出层反向计算到第一个隐层，并按照某种能使误差向减小方向发展的原则，调整网络中各神经元的连接权值。

      (6). 对训练样例集中的每一个样例重复(3)-(5)的步骤，直到对整个训练样例集的误差达到要求时为止。

      在以上的学习过程中，第(5)步是最重要的，如何确定一种调整连接权值的原则，使误差沿着减小的方向发展，是B-P学习算法必须解决的问题。

      B-P算法的优缺点：

      优点：理论基础牢固，推导过程严谨，物理概念清晰，通用性好等。所以，它是目前用来训练前向多层网络较好的算法。

      缺点：(1). 该学习算法的收敛速度慢；(2). 网络中隐节点个数的选取尚无理论上的指导；(3). 从数学角度看，B-P算法是一种梯度最速下降法，这就可能出现局部极小的问题。当出现局部极小时，从表面上看，误差符合要求，但这时所得到的解并不一定是问题的真正解。所以B-P算法是不完备的。

      BP算法局限性：

      (1). 在误差曲面上有些区域平坦，此时误差对权值的变化不敏感，误差下降缓慢，调整时间长，影响收敛速度。这时误差的梯度变化很小，即使权值的调整量很大，误差仍然下降很慢。造成这种情况的原因与各节点的净输入过大有关。

      (2). 存在多个极小点。从两维权空间的误差曲面可以看出，其上存在许多凸凹不平，其低凹部分就是误差函数的极小点。可以想象多维权空间的误差曲面，会更加复杂，存在更多个局部极小点，它们的特点都是误差梯度为0。BP算法权值调整依据是误差梯度下降，当梯度为0时，BP算法无法辨别极小点性质，因此训练常陷入某个局部极小点而不能自拔，使训练难以收敛于给定误差。

      BP算法改进：误差曲面的平坦区将使误差下降缓慢，调整时间加长，迭代次数增多，影响收敛速度；而误差曲面存在的多个极小点会使网络训练陷入局部极小，从而使网络训练无法收敛于给定误差。这两个问题是BP网络标准算法的固有缺陷。

      针对此，国内外不少学者提出了许多改进算法，几种典型的改进算法：

      (1). 增加动量项：标准BP算法在调整权值时，只按t时刻误差的梯度下降方向调整，而没有考虑t时刻以前的梯度方向，从而常使训练过程发生振荡，收敛缓慢。为了提高训练速度，可以在权值调整公式中加一动量项。大多数BP算法中都增加了动量项，以至于有动量项的BP算法成为一种新的标准算法。

      (2). 可变学习速度的反向传播算法（variable learning rate back propagation，VLBP）：多层网络的误差曲面不是二次函数。曲面的形状随参数空间区域的不同而不同。可以在学习过程中通过调整学习速度来提高收敛速度。技巧是决定何时改变学习速度和怎样改变学习速度。可变学习速度的VLBP算法有许多不同的方法来改变学习速度。

      (3). 学习速率的自适应调节：可变学习速度VLBP算法，需要设置多个参数，算法的性能对这些参数的改变往往十分敏感，另外，处理起来也较麻烦。此处给出一简洁的学习速率的自适应调节算法。学习率的调整只与网络总误差有关。学习速率η也称步长，在标准BP中是一常数，但在实际计算中，很难给定出一个从始至终都很合适的最佳学习速率。从误差曲面可以看出，在平坦区内η太小会使训练次数增加，这时候希望η值大一些；而在误差变化剧烈的区域，η太大会因调整过量而跨过较窄的“凹坑”处，使训练出现振荡，反而使迭代次数增加。为了加速收敛过程，最好是能自适应调整学习率η，使其该大则大，该小则小。比如可以根据网络总误差来调整.

      (4). 引入陡度因子—-防止饱和：误差曲面上存在着平坦区。其权值调整缓慢的原因在于S转移函数具有饱和特性造成的。如果在调整进入平坦区后，设法压缩神经元的净输入，使其输出退出转移函数的饱和区，就可改变误差函数的形状，从而使调整脱离平坦区。实现这一思路的具体作法是在转移函数中引进一个陡度因子。

      BP神经网络设计的一般原则：关于它的开发设计，大多数是根据使用者的经验来设计网络结构﹑功能函数﹑学习算法﹑样本等。

      [1]. BP网络参数设计

      (1). BP网络输入与输出参数的确定

      A. 输入量的选择：

      a. 输入量必须选择那些对输出影响大且能够检测或提取的变量；

      b. 各输入量之间互不相关或相关性很小。从输入、输出量性质分类来看，可以分为两类：数值变量和语言变量。数值变量又分为连续变量或离散变量。如常见的温度，压力，电压，电流等就是连续变量；语言变量是用自然语言表示的概念。如红，绿，蓝；男，女；大，中，小，开，关，亮，暗等。一般来说，语言变量在网络处理时，需要转化为离散变量。

      c. 输入量的表示与提取：多数情况下，直接送给神经网络的输入量无法直接得到，常常需要用信号处理与特征提取技术从原始数据中提取能反映其特征的若干参数作为网络输入。

      B. 输出量选择与表示：

      a. 输出量一般代表系统要实现的功能目标，如分类问题的类别归属等；

      b. 输出量表示可以是数值也可是语言变量；

      (2). 训练样本集的设计

      网络的性能与训练用的样本密切相关，设计一个好的训练样本集既要注意样本规模，又要注意样本质量。

      A. 样本数目的确定：一般来说样本数n越多，训练结果越能正确反映其内在规律，但样本的获取往往有一定困难，另一方面，当样本数n达到一定数量后，网络的精度也很难提高。

      选择原则：网络规模越大，网络映射关系越复杂，样本数越多。一般说来，训练样本数是网络连接权总数的5～10倍，但许多情况难以达到这样的要求。

      B. 样本的选择和组织：

      a. 样本要有代表性，注意样本类别的均衡；

      b. 样本的组织要注意将不同类别的样本交叉输入；

      c. 网络的训练测试，测试标准是看网络是否有好的泛化能力。测试做法：不用样本训练集中数据测试。一般是将收集到的可用样本随机地分成两部分，一部分为训练集，另一部分为测试集。若训练样本误差很小，而对测试集的样本误差很大，泛化能力差。

      (3). 初始权值的设计

      网络权值的初始化决定了网络的训练从误差曲面的哪一点开始，因此初始化方法对缩短网络的训练时间至关重要。

      神经元的作用函数是关于坐标点对称的，若每个节点的净输入均在零点附近，则输出均出在作用函数的中点，这个位置不仅远离作用函数的饱和区，而且是其变化最灵敏的区域，必使网络学习加快。从神经网络净输入表达式来看，为了使各节点的初始净输入在零点附近，如下两种方法被常常使用：

      A. 取足够小的初始权值；

      B. 使初始值为+1和-1的权值数相等。

      [2]. BP网络结构参数设计

      隐层结构设计

      (1). 隐层数设计：理论证明，具有单隐层的前馈网络可以映射所有连续函数，只有当学习不连续函数时才需要两个隐层，故一般情况隐层最多需要两层。一般方法是先设一个隐层，当一个隐层的节点数很多，仍不能改善网络性能时，再增加一个隐层。最常用的BP神经网络结构是3层结构，即输入层﹑输出层和1个隐层。

      (2). 隐层节点数设计：隐层节点数目对神经网络的性能有一定的影响。隐层节点数过少时，学习的容量有限，不足以存储训练样本中蕴涵的所有规律；隐层节点过多不仅会增加网络训练时间，而且会将样本中非规律性的内容如干扰和噪声存储进去。反而降低泛化能力。一般方法是凑试法：

      6. Hopfield模型：

      Hopfield模型是霍普菲尔德分别于1982年及1984提出的两个神经网络模型。1982年提出的是离散型，1984年提出的是连续型，但它们都是反馈网络结构。

      由于在反馈网络中，网络的输出要反复地作为输入再送入网络中，这就使得网络具有了动态性，网络的状态在不断的改变之中，因而就提出了网络的稳定性问题。所谓一个网络是稳定的是指从某一时刻开始，网络的状态不再改变。

      设用X(t)表示网络在时刻t的状态，如果从t=０的任一初态X(0)开始，存在一个有限的时刻t，使得从此时刻开始神经网络的状态不再发生变化，就称此网络是稳定的。

      离散网络模型是一个离散时间系统，每个神经元只有两个状态，可以用1和0来表示，由连接权值Ｗij所构成的矩阵是一个对角线为0的对称矩阵。

      Hopfield网络离散模型有两种工作模式：

      (1). 串行方式，是指在任一时刻t，只有一个神经元i发生状态变化，而其余的神经元保持状态不变。

      (2). 并行方式，是指在任一时刻t，都有部分或全体神经元同时改变状态。

       有关离散的Hopfield网络的稳定性问题，已于1983年由Cohen和Grossberg给于了证明。而Hopfield等人又进一步证明，只要连接权值构成的矩阵是非负对角元的对称矩阵，则该网络就具有串行稳定性。

      1984年，Hopfield又提出了连续时间的神经网络，在这种神经网络中，各节点可在0到1的区间内取任一实数值。

      Hopfield网络是一种非线性的动力网络，可通过反复的网络动态迭代来求解问题，这是符号逻辑方法所不具有的特性。在求解某些问题时，其求解问题的方法与人类求解问题的方法很相似，虽然所求得的解不是最佳解，但其求解速度快，更符合人们日常解决问题的策略。

      Hopfield递归网络是美国加洲理工学院物理学家J.J.Hopfield教授于1983年提出的。Hopfield网络按网络输入和输出的数字形式不同可分为离散型和连续型两种网络,即：离散型Hopfield神经网络—-DHNN(Discrete Hopfield Neural Network)；连续型Hopfield神经网络—-CHNN(ContinuesHopfield Neural Network)。

      DHNN结构：它是一种单层全反馈网络,共有n个神经元。每个神经元都通过连接权接收所有其它神经元输出反馈来的信息，其目的是为了让任一神经元的输出能接受所有神经元输出的控制,从而使各神经元能相互制约。

      DHNN的设计原则：吸引子的分布是由网络的权值（包括阀值）决定的，设计吸引子的核心就是如何设计一组合适的权值。为了使所设计的权值满足要求，权值矩阵应符合以下要求：(1)、为保证异步方式工作时网络收敛，W应为对称阵；(2)、为保证同步方式工作时网络收敛，W应为非负定对称阵；(3)、保证给定的样本是网络的吸引子，并且要有一定的吸引域。

      具体设计时，可以采用不同的方法：(1)、联立方程法；(2)、外积和法。

      CHNN：在连续型Hopfield神经网络中，所有神经元都随时间t并行更新，网络状态随时间连续改变。

      Hopfield网络的主要功能

      Hopfield神经网络的提出就是与其实际应用密切相关。其主要功能在以下两个方面。

      (1). 联想记忆：输入–输出模式的各元素之间，并不存在一对一的映射关系，输入–输出模式的维数也不要求相同；联想记忆时，只给出输入模式部分信息，就能联想出完整的输出模式。即具有容错性。

      (2). CHNN的优化计算功能.

      应用Hopfield 神经网络来解决优化计算问题的一般步骤为：

      A. 分析问题：网络输出与问题的解相对应。

      B. 构造网络能量函数：构造合适的网络能量函数，使其最小值对应问题最佳解。

      C. 设计网络结构：将能量函数与标准式相比较，定出权矩阵与偏置电流。

      D. 由网络结构建立网络的电子线路并运行，稳态–优化解或计算机模拟运行。

      7. BAM模型

      神经网络的联想记忆功能可以分为两种，一是自联想记忆，另一种是异联想记忆。Hopfield神经网络就属于自联想记忆。由Kosko B.1988 年提出的双向联想记忆神经网络BAM(Bidirectional Associative Memory)属于异联想记忆。BAM有离散型﹑连续型和自适应型等多种形式。

      8. CMAC模型

      BP神经网络﹑Hopfield神经网络和BAM双向联想记忆神经网络分别属于前馈和反馈神经网络，这主要是从网络的结构来划分的。如果从神经网络的函数逼近功能这个角度来分，神经网络可以分为全局逼近网络和局部逼近网络。当神经网络的一个或多个可调参数（权值和阈值）在输入空间的每一点对任何一个输出都有影响，则称该神经网络为全局逼近网络，多层前馈BP网络是全局逼近网络的典型例子。对于每个输入输出数据对，网络的每一个连接权均需进行调整，从而导致全局逼近网络学习速度很慢，对于有实时性要求的应用来说常常是不可容忍的。如果对网络输入空间的某个局部区域只有少数几个连接权影响网络输出，则称网络为局部逼近网络。对于每个输入输出数据对，只有少量的连接权需要进行调整，从而使局部逼近网络具有学习速度快的优点，这一点对于有实时性要求的应用来说至关重要。目前常用的局部逼近神经网络有CMAC网络、径向基函数RBF网络和B样条网络等，其结构原理相似。

      1975年J.S.Albus提出一种模拟小脑功能的神经网络模型，称为Cerebellar Model Articulation Controller，简称CMAC。CMAC网络是仿照小脑控制肢体运动的原理而建立的神经网络模型。小脑指挥运动时具有不假思索地作出条件反射迅速响应的特点，这种条件反射式响应是一种迅速联想。

      CMAC 网络有三个特点：

      (1). 作为一种具有联想功能的神经网络，它的联想具有局部推广（或称泛化）能力，因此相似的输入将产生相似的输出，远离的输入将产生独立的输出；

      (2). 对于网络的每一个输出，只有很少的神经元所对应的权值对其有影响，哪些神经元对输出有影响则有输入决定；

      (3). CMAC的每个神经元的输入输出是一种线性关系，但其总体上可看做一种表达非线性映射的表格系统。由于CMAC网络的学习只在线性映射部分，因此可采用简单的δ算法，其收敛速度比BP算法快得多，且不存在局部极小问题。CMAC最初主要用来求解机械手的关节运动，其后进一步用于机械人控制、模式识别、信号处理以及自适应控制等领域。

      9. RBF模型

      对局部逼近神经网络，除CMAC神经网络外，常用的还有径向基函数RBF网络和B样条网络等。径向基函数（RBF，Radial Basis Function）神经网络，是由J.Moody 和C.Darken于20世纪80年代末提出的一种神经网络，径向基函数方法在某种程度上利用了多维空间中传统的严格插值法的研究成果。在神经网络的背景下，隐藏单元提供一个“函数”集，该函数集在输入模式向量扩展至隐层空间时为其构建了一个任意的“基”；这个函数集中的函数就被称为径向基函数。径向基函数首先是在实多变量插值问题的解中引入的。径向基函数是目前数值分析研究中的一个主要领域之一。

      最基本的径向基函数（RBF）神经网络的构成包括三层，其中每一层都有着完全不同的作用。输入层由一些感知单元组成，它们将网络与外界环境连接起来；第二层是网络中仅有的一个隐层，它的作用是从输入空间到隐层空间之间进行非线性变换，在大多数情况下，隐层空间有较高的维数；输出层是线性的，它为作用于输入层的激活模式提供响应。

      基本的径向基函数RBF网络是具有单稳层的三层前馈网络。由于它模拟了人脑中局部调整、相互覆盖接受域（或称感受域，Receptive Field）的神经网络结构，因此，RBF网络是一种局部逼近网络，现已证明它能以任意精度逼近任一连续函数.

      RBF网络的常规学习算法，一般包括两个不同的阶段：

      (1). 隐层径向基函数的中心的确定阶段。常见方法有随机选取固定中心法；中心的自组织选择法等。

      (2). 径向基函数权值学习调整阶段。常见方法有中心的监督选择法；正则化严格插值法等。

      10. SOM模型

      芬兰Helsink大学Kohonen T.教授提出一种自组织特征映射网络SOM(Self-organizing feature Map)，又称Kohonen网络。Kohonen认为，一个神经网络接受外界输入模式时，将会分为不同的对应区域，各区域对输入模式有不同的响应特征，而这个过程是自动完成的。SOM网络正是根据这一看法提出的，其特点与人脑的自组织特性相类似。

      自组织神经网络结构

      (1). 定义：自组织神经网络是无导师学习网络。它通过自动寻找样本中的内在规律和本质属性，自组织、自适应地改变网络参数与结构。

      (2). 结构：层次型结构，具有竞争层。典型结构：输入层＋竞争层。

      输入层：接受外界信息，将输入模式向竞争层传递，起“观察”作用。

      竞争层：负责对输入模式进行“分析比较，寻找规律，并归类。

      自组织神经网络的原理

      (1). 分类与输入模式的相似性：分类是在类别知识等导师信号的指导下，将待识别的输入模式分配到各自的模式类中，无导师指导的分类称为聚类，聚类的目的是将相似的模式样本划归一类，而将不相似的分离开来，实现模式样本的类内相似性和类间分离性。由于无导师学习的训练样本中不含期望输出，因此对于某一输入模式样本应属于哪一类并没有任何先验知识。对于一组输入模式，只能根据它们之间的相似程度来分为若干类，因此，相似性是输入模式的聚类依据。

      (2). 相似性测量：神经网络的输入模式向量的相似性测量可用向量之间的距离来衡量。常用的方法有欧氏距离法和余弦法两种。

      (3). 竞争学习原理:竞争学习规则的生理学基础是神经细胞的侧抑制现象：当一个神经细胞兴奋后，会对其周围的神经细胞产生抑制作用。最强的抑制作用是竞争获胜的“唯我独兴”，这种做法称为“胜者为王”，（Winner-Take-All）。竞争学习规则就是从神经细胞的侧抑制现象获得的。它的学习步骤为：A、向量归一化；B、寻找获胜神经元；C、网络输出与权调整；D、重新归一化处理。

      SOM网络的拓扑结构：SOM网络共有两层。即：输入层和输出层。

      (1). 输入层：通过权向量将外界信息汇集到输出层各神经元。输入层的形式与BP网相同，节点数与样本维数相同。

      (2). 输出层：输出层也是竞争层。其神经元的排列有多种形式。分为一维线阵,二维平面阵和三维栅格阵。最典型的结构是二维形式。它更具大脑皮层的形象。

      输出层的每个神经元同它周围的其他神经元侧向连接，排列成棋盘状平面；输入层为单层神经元排列。

      SOM权值调整域

      SOM网采用的算法，称为Kohonen算法，它是在胜者为王WTA(Winner-Take-All)学习规则基础上加以改进的，主要区别是调整权向量与侧抑制的方式不同：WTA：侧抑制是“封杀”式的。只有获胜神经元可以调整其权值，其他神经元都无权调整。Kohonen算法：获胜神经元对其邻近神经元的影响是由近及远，由兴奋逐渐变为抑制。换句话说，不仅获胜神经元要调整权值，它周围神经元也要不同程度调整权向量。

      SOM网络运行原理

      SOM网络的运行分训练和工作两个阶段。在训练阶段，网络随机输入训练集中的样本，对某个特定的输入模式，输出层会有某个节点产生最大响应而获胜，而在训练开始阶段，输出层哪个位置的节点将对哪类输入模式产生最大响应是不确定的。当输入模式的类别改变时，二维平面的获胜节点也会改变。获胜节点周围的节点因側向相互兴奋作用也产生较大影响，于是获胜节点及其优胜邻域内的所有节点所连接的权向量均向输入方向作不同程度的调整，调整力度依邻域内各节点距离获胜节点的远近而逐渐减小。网络通过自组织方式，用大量训练样本调整网络权值，最后使输出层各节点成为对特定模式类敏感的神经元，对应的内星权向量成为各输入模式的中心向量。并且当两个模式类的特征接近时，代表这两类的节点在位置上也接近。从而在输出层形成能反应样本模式类分布情况的有序特征图。

      11. CPN模型

      1987年美国学者RobertHecht —Nielson提出了对偶传播神经网络(Counter–propagation Networks，简记为CPN)。CPN最早是用来实现样本选择匹配系统的。它能存储二进制或模拟值的模式对，因此CPN网络可以用作联想存储﹑模式分类﹑函数逼近和数据压缩等用途。与BP网相比，CPN的训练速度要快很多，所需的时间大约是BP网所需时间的1％。但是，它的应用面却因网络的性能相对来说比较窄。

      从网络的拓扑结构来看，CPN与BP网类似，CPN是一个三层的神经网络，只不过这竞争层和输出层执行的训练算法是不同的。所以，称CPN 是一个异构网。与同构网相比，网络的异构性使它更接近于人脑。在人脑中存在有各种特殊的模块，它们使用完成不同的运算。例如，在听觉通道的每一层，其神经元与神经纤维在结构上的排列与频率的关系十分密切，对某一些频率，其中某些相应的神经元会获得最大的响应。这种听觉通道上的神经元的有序排列一直延续到听觉皮层。尽管许多低层次上的神经元是预先排列好的，但高层次上的神经元的组织则是通过学习自组织形成的。

      在RobertHecht—Nielson提出的CPN神经网络中，其竞争层和输出层分别执行较早些时候出现的两个著名算法：即Kohonen l981年提出的自组织映射SOM算法和Grossberg l969年提出的外星(Outstar)算法。人们将执行自组织映射的层称为Kohonen层，执行外星算法的层则被称为Grossberg层。按这种方法将这两种算法组合在一起后所获得的网络，不仅提供了一种设计多级网训练算法的思路，解决了多级网络的训练问题，突破了单极网的限制，而且还使得网络具有了许多新的特点。多级网络的训练问题主要是在解决隐藏层神经元相应的联接权调整时，需要通过隐藏层神经元的理想输出来实现相关误差的估计。然而，它们对应的理想输出又是未知的。在无导师训练中是不需要知道理想输出的，因此可以考虑让网络的隐藏层执行无导师学习。这是解决多级网络训练的另一个思路。实际上，CPN就是将无导师训练算法与有导师训练算法结合在一起，用无导师训练解决网络隐藏层的理想输出未知的问题，用有导师训练解决输出层按系统的要求给出指定的输出结果的问题。

      Kohonen提出的自组织映射由四部分组成，包括一个神经元阵列(用它构成CPN的Kohonen层)，一种比较选择机制，一个局部互联，一个自适应过程。实际上，这一层将实现对输入进行分类的功能。所以，该层可以执行无导师的学习，以完成对样本集中所含的分类信息的提取。

      Grossberg层主要用来实现类表示。由于相应的类应该是用户所要求的，所以，对应每—个输入向量，用户明确地知道它对应的理想输出向量，故该层将执行有导师的训练。两层的有机结合，就构成—个映射系统。所以，有人将CPN 看成一个有能力进行一定的推广的查找表(Look—up table)。它的训练过程就是将输入向量与相应的输出向量对应起来。这些向量可以是二值的，也可以是连续的。一旦网络完成了训练，对一个给定的输入就可以给出一个对应的输出。网络的推广能力表明，当网络遇到一个不太完整的、或者是不完全正确的输入时，只要该“噪音”是在有限的范围内，CPN 都可以产生一个正确的输出。这是因为Kohonen 层可以找到这个含有噪音的输入应该属于的分类，而对应的Grossberg层则可以给出该分类的表示。从整个网络来看，就表现出一种泛化能力。这使得网络在模式识别、模式完善、信号处理等方面可以有较好的应用。另外，上述映射的逆映射如果存在的话，可以通过对此网的简单扩展，来实现相应的逆变换。这被称为全对传网。

      12. ART模型

      在神经网络学习中，当网络规模给定后，由权矩阵所能记忆的模式类别信息量总是有限的，新输入的模式样本必然会对已经记忆的模式样本产生抵消或遗忘，从而使网络的分类能力受到影响。靠无限扩大网络规模解决上述问题是不现实的。如何保证在适当增加网络规模的同时，在过去记忆的模式和新输入的训练模式之间作出某种折中，既能最大限度地接收新的模式信息，同时又能保证较少地影响过去的样本模式呢？ ART网络在一定程度上能较好解决此问题。

      1976年，美国Boston大学CarpenterG.A.教授提出了自适应共振理论ART(Adaptive Resonance Theory)。随后Carpenter G.A.又与他的学生GrossbergS.合作提出了ART神经网络。

      经过多年的研究和发展，ART 网络已有几种基本形式：

      (1). ART1型神经网络：处理双极性和二进制信号；

      (2). ART2型神经网络：它是ART1型的扩展，用于处理连续型模拟信号；

      (3). ART综合系统：将ART1和ART2综合在一起，系统具有识别﹑补充和撤消等综合功能。即所谓的3R（Recognition﹑Reinforcement﹑Recall）功能。

      (4). ART3型神经网络：它是一种分级搜索模型，兼容前两种结构的功能并将两层神经网络扩大为任意多层神经元网络，由于ART3型在神经元的模型中纳入了生物神经元的生物电－化学反应机制，因而它具备了很强的功能和扩展能力。

      13. 量子神经网络

      量子神经网络的概念出现于上个世纪90年代后期，一经提出后便引起了不同领域的科学家的关注，人们在这个崭新的领域进行了不同方向的探索，提出了很多想法和初步的模型，充分体现了量子神经网络研究的巨大潜力。主要研究方向可以概括为：

      (1). 量子神经网络采用神经网络的连接思想来构造量子计算机，通过神经网络模型来研究量子计算中的问题；

      (2). 量子神经网络在量子计算机或量子器件的基础上构造神经网络，充分利用量子计算超高速、超并行、指数级容量的特点，来改进神经网络的结构和性能；

      (3). 量子神经网络作为一种混合的智能优化算法在传统的计算机上的实现，通过引入量子理论中的思想对传统神经网络改进，利用量子理论中的概念、方法(如态叠加、“多宇宙”观点等)，建立新的网络模型；改善传统神经网络的结构和性能；

      (4). 基于脑科学、认知科学的研究。

      以上整理的内容主要摘自：

      1.《人工神经网络原理及应用》，2006，科学出版社

      2.《神经网络邮件分类算法研究》，2011，硕论，电子科技大学

      3. 《人工神经网络原理、分类及应用》，2014，期刊，科技资讯

      关于BP神经网络的实现可以参考： BP神经网络公式推导及实现(MNIST)_网络资源是无限的-CSDN博客 

      GitHub： GitHub – fengbingchun/NN_Test: This project contains some neural network code 

今天的文章人工神经网络简介分享到此就结束了，感谢您的阅读。