A*算法之八数码问题 python解法

系列文章

• 人工智能 倒啤酒问题 python解法
• 人工智能 水壶问题 python解法
• A*算法之八数码问题 python解法
• A*算法之野人传教士问题 python解法
• 人工智能 遗传算法 计算函数极值问题

人工智能课程中学习了A*算法,在耗费几小时完成了八数码问题和野人传教士问题之后,决定写此文章来记录一下,避免忘记

问题描述

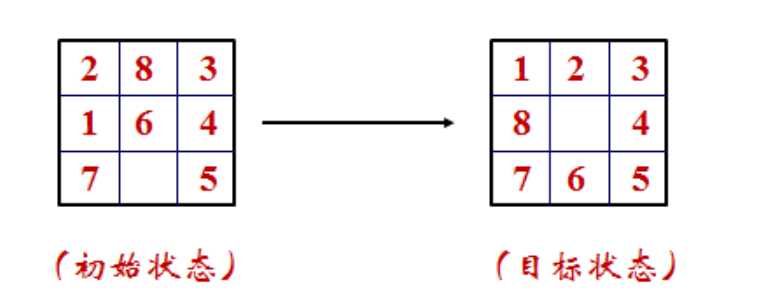
在3×3的棋盘上，摆有八个棋子，每个棋子上标有1至8的某一数字。棋盘中留有一个空格，空格用0来表示。空格周围的棋子可以移到空格中。要求解的问题是：给出一种初始布局（初始状态）和目标布局（为了使题目简单,设目标状态为123804765），找到一种最少步骤的移动方法，实现从初始布局到目标布局的转变。
也就是移动下图中的方块,使得九宫格可以恢复到目标的状态

A*算法与八数码问题

主要来介绍一下A*算法与该题目如何结合使用,并且使用python语言来实现它

首先对于A*算法,来做一个简单的介绍

那么对于八数码问题,我们需要做的是把他和A*问题联系在一起
这里就需要解决3个问题

1. 状态空间的定义
2. 各种操作的定义
3. 启发式函数的定义

状态空间的定义

首先,本题的状态空间已经很明确了, 就是一个3*3的九宫格,里面充满1-8的数字,加上一个空格,为了方便表示,我们可以把空格用0来表示
那么状态空间就可以用数组来表示(这里使用numpy来表示)

import numpy as np
start_data = np.array([[2, 8, 3], [1, 6, 4], [7, 0, 5]])
end_data = np.array([[1, 2, 3], [8, 0, 4], [7, 6, 5]])

各种操作的定义

对于操作,可以理解为更改状态空间的一些规则
很容易就能想到,如果以每一个元素为对象来讨论,那么它们的上下左右移动最后导致的数组元素交换会稍稍有些复杂,我们不如换一个角度,从空格的移动来考虑
那么操作(转换规则如下所示)

1. 空格上移
2. 空格下移
3. 空格左移
4. 空格右移

当然,这些移动还需要判断一些因素,因为有些情况是无法移动的

如上图情况下就不能下移,所以可以编写一个函数来表示各种操作及其产生的影响
注: 下面代码是我自己写的,仅供参考,建议按自己的思路写一遍

def find_zero(num):
    tmp_x, tmp_y = np.where(num == 0)
    # 返回0所在的x坐标与y坐标
    return tmp_x[0], tmp_y[0]
def swap(num_data, direction):
    x, y = find_zero(num_data)
    num = np.copy(num_data)
    if direction == 'left':
        if y == 0:
            # print('不能左移')
            return num
        num[x][y] = num[x][y - 1]
        num[x][y - 1] = 0
        return num
    if direction == 'right':
        if y == 2:
            # print('不能右移')
            return num
        num[x][y] = num[x][y + 1]
        num[x][y + 1] = 0
        return num
    if direction == 'up':
        if x == 0:
            # print('不能上移')
            return num
        num[x][y] = num[x - 1][y]
        num[x - 1][y] = 0
        return num
    if direction == 'down':
        if x == 2:
            # print('不能下移')
            return num
        else:
            num[x][y] = num[x + 1][y]
            num[x + 1][y] = 0
            return num

测试一下

num = np.array([[1, 2, 3], [8, 0, 4], [7, 6, 5]])
print('初始状态:')
print(num)
print('-' * 50)
print('左移')
print(swap(num, 'left'))
print('-' * 50)
print('右移')
print(swap(num, 'right'))
print('-' * 50)
print('上移')
print(swap(num, 'up'))
print('-' * 50)
print('下移')
print(swap(num, 'down'))
print('-' * 50)

初始状态:
[[1 2 3]
 [8 0 4]
 [7 6 5]]
--------------------------------------------------
左移
[[1 2 3]
 [0 8 4]
 [7 6 5]]
--------------------------------------------------
右移
[[1 2 3]
 [8 4 0]
 [7 6 5]]
--------------------------------------------------
上移
[[1 0 3]
 [8 2 4]
 [7 6 5]]
--------------------------------------------------
下移
[[1 2 3]
 [8 6 4]
 [7 0 5]]
--------------------------------------------------

Process finished with exit code 0

启发式函数的定义

$$f(n)=d(n)+w(n)$$

其中$d(n)$为搜索树的深度,也可以理解为当前是第几轮循环
$w(n)$为当前状态到目标状态的实际最小费用的估计值, 在八数码问题中,可以采用放错位置的数字个数,也可以采用数字到正确位置的曼哈顿距离,因人而异
在本文中采用的是 w(n)=放错位置的数字个数

如果将空格位置的正误计算进入,则函数如下

def cal_wcost(num):
    return sum(sum(num != end_data))

如果不将空格位置的正误计算进入,则函数如下

def cal_wcost(num):
        return sum(sum(num != end_data)) - int(num[1][1] != 0)

也可以用思路最简单的遍历方法

def cal_wcost(num):
    ''' 计算w(n)的值,及放错元素的个数 :param num: 要比较的数组的值 :return: 返回w(n)的值 '''
    con = 0
    for i in range(3):
        for j in range(3):
            tmp_num = num[i][j]
            compare_num = end_data[i][j]
            if tmp_num != 0:
                con += tmp_num != compare_num
    return con

A*算法代码框架

先给出我自己定义的代码框架,如果感兴趣的朋友可以用自己的思路去完善它

import queue
opened = queue.Queue()  # open表
closed = { 
   }  # close表
def method_a_function():
    while len(opened.queue) != 0:
    	# 取队首元素
        node = opened.get()
        # 判断是否为目标值.是则返回正确值
        1.这里需要一条代码/函数
        # 将取出的点加入closed表中
        2.这里需要一条代码/函数
        # 产生取出元素的一切后继,即执行四个操作
        for action in ['left', 'right', 'up', 'down']:
            # 创建子节点
            3.这里需要一条代码/函数
            # 判断是否在closed表中
            4.这里需要一条代码/函数
            	#如果不在close表中,将其加入opened表
            	5.这里需要一条代码/函数(并且考虑到与opened表中已有元素重复的更新情况)
        # 排序
        '''为open表进行排序,根据其中的f_loss值'''
        6.这里需要一条代码/函数

A*算法代码代码详解

根据上面的框架,我们可以一步一步的来完善它

位置1函数

只要判断一下是否相等就可以了,非常简单

if (node.data == end_data).all():
    return node

一、Node类

首先我创建了一个Node类 ,它具有如下一些属性

• data很明显用来记录当前的状态
• step用来记录当前的步数,也就是 g(n) :初始状态到当前状态的距离
• parent用来记录父节点 (这样可以在得到结论之后通过遍历来获取所有的父节点,从而得到最佳路径)
• f_loss用来计算f(n)的值

# 创建Node类 (包含当前数据内容,父节点,步数)
class Node:
    f_loss = -1  # 启发值
    step = 0  # 初始状态到当前状态的距离（步数）
    parent = None,  # 父节点

    # 用状态和步数构造节点对象
    def __init__(self, data, step, parent):
        self.data = data  # 当前状态数值
        self.step = step
        self.parent = parent
        # 计算f(n)的值
        self.f_loss = cal_wcost(data) + step

那么就可以创建初始节点,并且加入opened表中

start_data = np.array([[2, 8, 3], [1, 6, 4], [7, 0, 5]])
opened = queue.Queue()  # open表
start_node = Node(start_data, 0, None)
opened.put(start_node)

位置3函数

child_node = Node(swap(node.data, action), node.step + 1, node)

二、data_to_int函数

在这里,我定义closed表为一个字典,因为它的键不能放numpy.array,所以我手动写了一个函数把numpy的数组转换为一个int类型的数字
这里的函数类似于hash函数,不一定要跟我一样,只要保证各种状态产生的结果不同即可

# 将data转化为不一样的数字 
def data_to_int(num):
    value = 0
    for i in num:
        for j in i:
            value = value * 10 + j
    return value

位置2的函数

closed[data_to_int(node.data)] = 1  # 奖取出的点加入closed表中

三、opened表的更新/插入

这里要判断档要插入的节点是否已经在opened表中出现过,如果出现过,则f_loss更小的节点保留

# 编写一个比较当前节点是否在open表中,如果在,根据f(n)的大小来判断去留
def refresh_open(now_node):
    ''' :param now_node: 当前的节点 :return: '''
    tmp_open = opened.queue.copy()  # 复制一份open表的内容
    for i in range(len(tmp_open)):
        '''这里要比较一下node和now_node的区别,并决定是否更新'''
        data = tmp_open[i]
        now_data = now_node.data
        if (data == now_data).all():
            data_f_loss = tmp_open[i].f_loss
            now_data_f_loss = now_node.f_loss
            if data_f_loss <= now_data_f_loss:
                return False
            else:
                print('')
                tmp_open[i] = now_node
                opened.queue = tmp_open  # 更新之后的open表还原
                return True
    tmp_open.append(now_node)
    opened.queue = tmp_open  # 更新之后的open表还原
    return True

位置4,5的函数

index = data_to_int(child_node.data) # 获取当前节点转换后的index值
if index not in closed:
    refresh_open(child_node)

四、opened表排序

按照f_loss从小到大排序,这里我使用最传统的排序方法,有许多可以改进的地方,也可以用python的排序方法结合lambda函数来使用

# 编写一个给open表排序的函数
def sorte_by_floss():
    tmp_open = opened.queue.copy()
    length = len(tmp_open)
    # 排序,从小到大,当一样的时候按照step的大小排序
    for i in range(length):
        for j in range(length):
            if tmp_open[i].f_loss < tmp_open[j].f_loss:
                tmp = tmp_open[i]
                tmp_open[i] = tmp_open[j]
                tmp_open[j] = tmp
            if tmp_open[i].f_loss == tmp_open[j].f_loss:
                if tmp_open[i].step > tmp_open[j].step:
                    tmp = tmp_open[i]
                    tmp_open[i] = tmp_open[j]
                    tmp_open[j] = tmp
    opened.queue = tmp_open

位置6的函数

sorte_by_floss()

五、结果的输出

首先编写output_result函数,依次获取目标节点的父节点,形成一条正确顺序的路径
然后使用循环将这条路径输出
这里为了输出的好看,我使用了prettytable这个库,当然也可以直接输出

def output_result(node):
    all_node = [node]
    for i in range(node.step):
        father_node = node.parent
        all_node.append(father_node)
        node = father_node
    return reversed(all_node)


node_list = list(output_result(result_node))
tb = pt.PrettyTable()
tb.field_names = ['step', 'data', 'f_loss']
for node in node_list:
    num = node.data
    tb.add_row([node.step, num, node.f_loss])
    if node != node_list[-1]:
        tb.add_row(['---', '--------', '---'])
print(tb)

总共耗费6轮
+------+-----------+--------+
| step |    data   | f_loss |
+------+-----------+--------+
|  0   |  [[2 8 3] |   4    |
|      |   [1 6 4] |        |
|      |  [7 0 5]] |        |
| ---  |  -------- |  ---   |
|  1   |  [[2 8 3] |   4    |
|      |   [1 0 4] |        |
|      |  [7 6 5]] |        |
| ---  |  -------- |  ---   |
|  2   |  [[2 0 3] |   5    |
|      |   [1 8 4] |        |
|      |  [7 6 5]] |        |
| ---  |  -------- |  ---   |
|  3   |  [[0 2 3] |   5    |
|      |   [1 8 4] |        |
|      |  [7 6 5]] |        |
| ---  |  -------- |  ---   |
|  4   |  [[1 2 3] |   5    |
|      |   [0 8 4] |        |
|      |  [7 6 5]] |        |
| ---  |  -------- |  ---   |
|  5   |  [[1 2 3] |   5    |
|      |   [8 0 4] |        |
|      |  [7 6 5]] |        |
+------+-----------+--------+

Process finished with exit code 0

六、代码

可能还是给全代码比较省力

# -*- coding: utf-8 -*-
# @Time : 2020/10/29 21:37
# @Author : Tong Tianyu
# @File : 八数码问题.py
# @Question: A* 算法解决八数码问题
import numpy as np
import queue
import prettytable as pt

''' 初始状态: 目标状态: 2 8 3 1 2 3 1 6 4 8 4 7 5 7 6 5 '''
start_data = np.array([[2, 8, 3], [1, 6, 4], [7, 0, 5]])
end_data = np.array([[1, 2, 3], [8, 0, 4], [7, 6, 5]])

'准备函数'




# 找空格(0)号元素在哪的函数
def find_zero(num):
    tmp_x, tmp_y = np.where(num == 0)
    # 返回0所在的x坐标与y坐标
    return tmp_x[0], tmp_y[0]


# 交换位置的函数 移动的时候要判断一下是否可以移动(是否在底部)
# 记空格为0号,则每次移动一个数字可以看做对空格(0)的移动,总共有四种可能

def swap(num_data, direction):
    x, y = find_zero(num_data)
    num = np.copy(num_data)
    if direction == 'left':
        if y == 0:
            # print('不能左移')
            return num
        num[x][y] = num[x][y - 1]
        num[x][y - 1] = 0
        return num
    if direction == 'right':
        if y == 2:
            # print('不能右移')
            return num
        num[x][y] = num[x][y + 1]
        num[x][y + 1] = 0
        return num
    if direction == 'up':
        if x == 0:
            # print('不能上移')
            return num
        num[x][y] = num[x - 1][y]
        num[x - 1][y] = 0
        return num
    if direction == 'down':
        if x == 2:
            # print('不能下移')
            return num
        else:
            num[x][y] = num[x + 1][y]
            num[x + 1][y] = 0
            return num


# 编写一个用来计算w(n)的函数
def cal_wcost(num):
    ''' 计算w(n)的值,及放错元素的个数 :param num: 要比较的数组的值 :return: 返回w(n)的值 '''
    # return sum(sum(num != end_data)) - int(num[1][1] != 0)
    con = 0
    for i in range(3):
        for j in range(3):
            tmp_num = num[i][j]
            compare_num = end_data[i][j]
            if tmp_num != 0:
                con += tmp_num != compare_num
    return con


# 将data转化为不一样的数字 类似于hash
def data_to_int(num):
    value = 0
    for i in num:
        for j in i:
            value = value * 10 + j
    return value


# 编写一个给open表排序的函数
def sorte_by_floss():
    tmp_open = opened.queue.copy()
    length = len(tmp_open)
    # 排序,从小到大,当一样的时候按照step的大小排序
    for i in range(length):
        for j in range(length):
            if tmp_open[i].f_loss < tmp_open[j].f_loss:
                tmp = tmp_open[i]
                tmp_open[i] = tmp_open[j]
                tmp_open[j] = tmp
            if tmp_open[i].f_loss == tmp_open[j].f_loss:
                if tmp_open[i].step > tmp_open[j].step:
                    tmp = tmp_open[i]
                    tmp_open[i] = tmp_open[j]
                    tmp_open[j] = tmp
    opened.queue = tmp_open


# 编写一个比较当前节点是否在open表中,如果在,根据f(n)的大小来判断去留
def refresh_open(now_node):
    ''' :param now_node: 当前的节点 :return: '''
    tmp_open = opened.queue.copy()  # 复制一份open表的内容
    for i in range(len(tmp_open)):
        '''这里要比较一下node和now_node的区别,并决定是否更新'''
        data = tmp_open[i]
        now_data = now_node.data
        if (data == now_data).all():
            data_f_loss = tmp_open[i].f_loss
            now_data_f_loss = now_node.f_loss
            if data_f_loss <= now_data_f_loss:
                return False
            else:
                print('')
                tmp_open[i] = now_node
                opened.queue = tmp_open  # 更新之后的open表还原
                return True
    tmp_open.append(now_node)
    opened.queue = tmp_open  # 更新之后的open表还原
    return True


# 创建Node类 (包含当前数据内容,父节点,步数)
class Node:
    f_loss = -1  # 启发值
    step = 0  # 初始状态到当前状态的距离（步数）
    parent = None,  # 父节点

    # 用状态和步数构造节点对象
    def __init__(self, data, step, parent):
        self.data = data  # 当前状态数值
        self.step = step
        self.parent = parent
        # 计算f(n)的值
        self.f_loss = cal_wcost(data) + step


'算法'
opened = queue.Queue()  # open表
start_node = Node(start_data, 0, None)
opened.put(start_node)

closed = { 
   }  # close表


def method_a_function():
    con = 0
    while len(opened.queue) != 0:
        node = opened.get()
        if (node.data == end_data).all():
            print(f'总共耗费{con}轮')
            return node

        closed[data_to_int(node.data)] = 1  # 奖取出的点加入closed表中
        # 四种移动方法
        for action in ['left', 'right', 'up', 'down']:
            # 创建子节点
            child_node = Node(swap(node.data, action), node.step + 1, node)
            index = data_to_int(child_node.data)
            if index not in closed:
                refresh_open(child_node)
        # 排序
        '''为open表进行排序,根据其中的f_loss值'''
        sorte_by_floss()
        con += 1


result_node = method_a_function()


def output_result(node):
    all_node = [node]
    for i in range(node.step):
        father_node = node.parent
        all_node.append(father_node)
        node = father_node
    return reversed(all_node)


node_list = list(output_result(result_node))
tb = pt.PrettyTable()
tb.field_names = ['step', 'data', 'f_loss']
for node in node_list:
    num = node.data
    tb.add_row([node.step, num, node.f_loss])
    if node != node_list[-1]:
        tb.add_row(['---', '--------', '---'])
print(tb)

今天的文章A*算法之八数码问题 python解法分享到此就结束了，感谢您的阅读。