上篇博客介绍了基于距离的K-Means聚类,这次给大家推荐一个基于密度的聚类算法:Meanshift(均值漂移)。
Meanshift 聚类基本原理
Meanshift 聚类的主要思路是:计算某一点A与其半径R内的点之间向量距离的平均值M,得到该点下一步的漂移(移动)方向(A=M+A)和距离(||M||)。当该点不再移动时,计算这个点与历史簇中心的距离,满足小于阈值D即合并为同一个类簇,不满足则自身形成一个类簇。直到所有的数据点选取完毕。
Meanshift 聚类流程简述
相比 K-Means 聚类,Meanshift 最大的优势是不需要人为指定分成几类。该算法会根据分布密度自动将数据归到适合的类中。
Meanshift 聚类算法的大致思想就是 “哪里人多哪里跑” :
首先,将所有数据点设置为未标价状态。
- 从未被标记的数据中随机选取一个点作为初始大佬(质心);
由于事先并不知道会聚成几类,所以只能一类一类的聚,最后聚成几类就几类了╮(╯▽╰)╭。 - 以当前大佬为圆心,半径为 R R R(超参1) 画个圆,圆内的点记做集合 M M M,里面为该位大佬的小弟;为了方便日后相认,大佬决定给小弟们一张带来自己标识的保命卡进行标记。
- 由于是随机选择的大佬,难以服众。这位大佬的小弟们提出要召开选举大会,选出新的大佬(即通过算法选出新的质心);
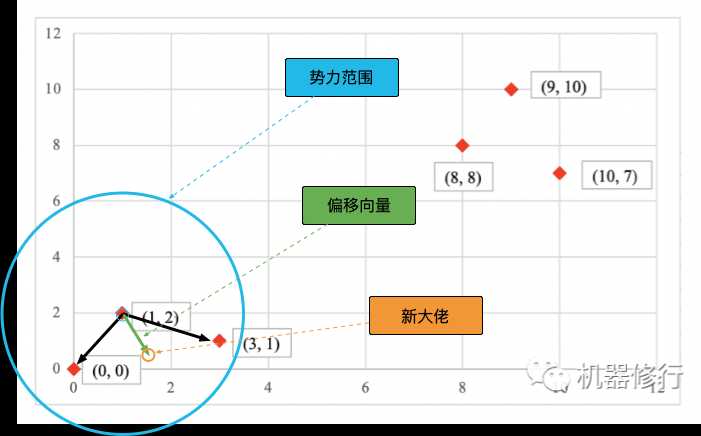
- 投票依据:这一届的小弟都很喜欢热闹,哪里人多就往哪边投。依次计算各位小弟到该大佬的向量距离(黑色向量)的平均值 s h i f t shift shift(绿色向量),如下图所示。
- 更新方式:旧大佬(蓝色圆圈)沿着投票方向即shift向量的方向移动,移动距离是||shift||,即为新大佬的位置(橙色圆圈)。也就是说这个大佬是“虚拟的”。
- 迭代2~3步骤,直到新大佬和旧大佬之间的偏移量小于某一个设置的阈值 δ \delta δ (超参2),即表示重新计算的质心的位置变化不大,趋于稳定,或者说收敛。从而得到一个候选大佬(还不是正式的哈,晋级之路漫漫其修远兮)。
- 比较这位候选大佬跟正式大佬的距离,若距离小于指定的阈值 ω \omega ω(超参3),则合并这两个大佬。否则,将该候选大佬提升为正式大佬,类别数加1;
- 迭代上述1~5步骤,直到所有数据点都被标记;
- 正式大佬全部确定下来后,小弟们就要选择投靠哪位大佬了。根据大佬在晋级路上发给小弟们的保命卡数量(即每个正式大佬对每个小弟的访问频数),小弟们选择投靠给自己保命卡最多的大佬(即对自己访问频数最大的那个大佬)。看样子小弟们还是很念旧情的哈。
- 注意:上面涉及的三个超参是需要用户人为指定的哈。
实例演示
看了上面的原理简述,估计还是有点糊涂,下面举一个非常形象简单的例子。
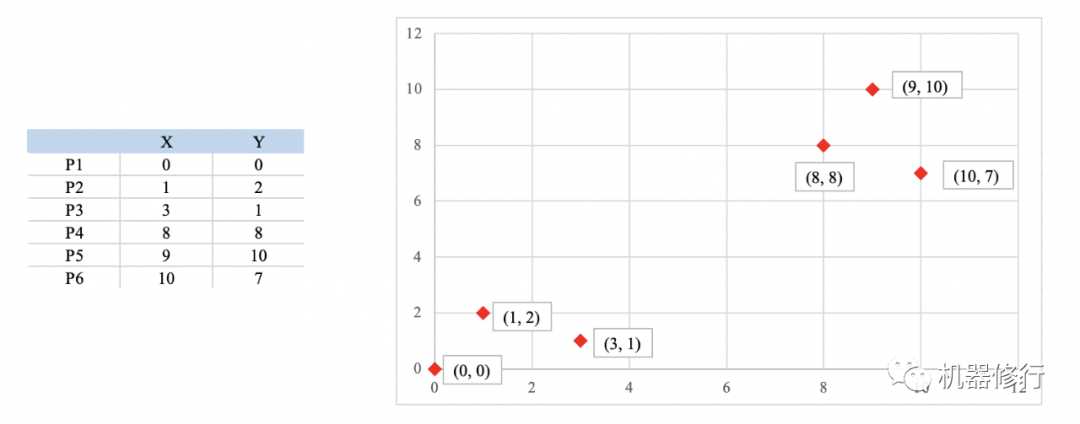
如下图所示,有6个点,从图上看应该可以分成两堆,前三个点一堆,后三个点另一堆。现在我手工地把MeanShift 算法的计算过程演示一下,同时检验是不是和预期一致:
-
随机选择一个初始大佬(就选 P2),开始它的晋级之路;
-
以 R = 5 R=5 R=5 为半径,圈定大佬的势力范围。在范围内的点 P1、P3 即为该大佬的小弟。大佬为了笼络小弟们的心,给范围内的小弟人手一张保命卡。此时所有数据点的保命符情况:
| 保命符 | P1 | P2 | P3 | P4 | P5 | P6 |
|---|---|---|---|---|---|---|
| 大佬1 | 1 | 0 | 1 | 0 | 0 | 0 |
-
召开选举大会,重新选大佬。
首先,计算各位小弟到该大佬的向量距离(黑色向量)的平均值 s h i f t shift shift。
| P1 | P3 | |
|---|---|---|
| 距离向量 | ( − 1 , − 2 ) (-1,-2) (−1,−2) | ( 2 , − 1 ) (2,-1) (2,−1) |
则, s h i f t = ( − 1 + 2 2 , − 2 − 1 2 ) = ( 0.5 , − 1.5 ) shift=(\dfrac{-1+2}{2}, \dfrac{-2-1}{2})=(0.5,-1.5) shift=(2−1+2,2−2−1)=(0.5,−1.5)
此时,旧大佬沿着shift向量的方向进行漂移,漂移长度为||shift||,即为新大佬 P 哥的位置: ( 1 , 2 ) + ( 0.5 , − 1.5 ) = ( 1.5 , 0.5 ) (1,2)+(0.5, -1.5) = (1.5, 0.5) (1,2)+(0.5,−1.5)=(1.5,0.5)
- 令超参 δ = 1 \delta=1 δ=1,由于上一步偏移距离 ∣ ∣ s h i f t ∣ ∣ = ( 0. 5 2 + ( − 1.5 ) 2 ) > δ ||shift||=\sqrt{(0.5^2+(-1.5)^2)}>\delta ∣∣shift∣∣=(0.52+(−1.5)2)>δ,所以再次以 R = 5 R=5 R=5 为半径,圈定大佬的势力范围。在范围内的点 P1、P2、P3 即为该大佬的小弟。大佬为了笼络小弟们的心,给范围内的小弟人手一张保命卡。此时所有数据点的保命符情况:
| 保命符 | P1 | P2 | P3 | P4 | P5 | P6 |
|---|---|---|---|---|---|---|
| 大佬1 | 2 | 1 | 2 | 0 | 0 | 0 |
- 第二届选举大会:
首先,计算各位小弟到该大佬的向量距离(黑色向量)的平均值 s h i f t shift shift
| P1 | P2 | P3 | |
|---|---|---|---|
| 距离向量 | ( − 1.5 , − 0.5 ) (-1.5,-0.5) (−1.5,−0.5) | ( − 0.5 , 1.5 ) (-0.5,1.5) (−0.5,1.5) | ( 1.5 , 0.5 ) (1.5,0.5) (1.5,0.5) |
则, s h i f t = ( − 1.5 − 0.5 + 1.5 3 , − 0.5 + 1.5 + 0.5 3 ) = ( − 0.5 / 3 , 0.5 ) shift=(\dfrac{-1.5-0.5+1.5}{3}, \dfrac{-0.5+1.5+0.5}{3})=(-0.5/3,0.5) shift=(3−1.5−0.5+1.5,3−0.5+1.5+0.5)=(−0.5/3,0.5)
同样的方法选出新的虚拟大佬:P哥 ( 1.5 , 0.5 ) + ( − 0.5 / 3 , 0.5 ) = ( 4 / 3 , 1 ) (1.5, 0.5)+(-0.5/3, 0.5) = (4/3, 1) (1.5,0.5)+(−0.5/3,0.5)=(4/3,1)。
-
由于上一步偏移距离 ∣ ∣ s h i f t ∣ ∣ = ( ( 0.5 / 3 ) 2 + ( 0.5 ) 2 ) < δ ||shift||=\sqrt{((0.5/3)^2+(0.5)^2)}<\delta ∣∣shift∣∣=((0.5/3)2+(0.5)2)<δ,当前的大佬 P 哥终于晋级为候选大佬了。
-
比较候选大佬 P 哥跟正式大佬的距离。由于目前还没有正式大佬,P哥直接晋级为正式大佬了,晋级之路结束。此时,所有数据点的保命符情况:
| 保命符 | P1 | P2 | P3 | P4 | P5 | P6 |
|---|---|---|---|---|---|---|
| 大佬1 | 2 | 1 | 2 | 0 | 0 | 0 |
-
回到第一步,从没有保命卡的数据里随机选一个当第二个初始大佬(就选 P4),开始它的晋级之路;
-
以 R = 5 R=5 R=5 为半径,圈定大佬的势力范围。在范围内的点 P5、P6 即为该大佬的小弟。大佬为了笼络小弟们的心,给范围内的小弟人手一张保命卡。此时所有数据点的保命符情况:
| 保命符 | P1 | P2 | P3 | P4 | P5 | P6 |
|---|---|---|---|---|---|---|
| 大佬2 | 0 | 0 | 0 | 0 | 1 | 1 |
-
召开选举大会,重新选大佬。
首先,计算各位小弟到该大佬的向量距离(黑色向量)的平均值 s h i f t shift shift。
| P5 | P6 | |
|---|---|---|
| 距离向量 | ( 1 , 2 ) (1,2) (1,2) | ( 2 , − 1 ) (2,-1) (2,−1) |
则, s h i f t = ( 1 + 2 2 , 2 − 1 2 ) = ( 1.5 , 0.5 ) shift=(\dfrac{1+2}{2}, \dfrac{2-1}{2})=(1.5,0.5) shift=(21+2,22−1)=(1.5,0.5)
此时,旧大佬沿着shift向量的方向进行漂移,漂移长度为||shift||,即为新大佬 P 哥的位置即为: ( 8 , 8 ) + ( 1.5 , 0.5 ) = ( 9.5 , 8.5 ) (8,8)+(1.5, 0.5) = (9.5, 8.5) (8,8)+(1.5,0.5)=(9.5,8.5)
- 由于上一步偏移距离 ∣ ∣ s h i f t ∣ ∣ = ( 1. 5 2 + ( 0.5 ) 2 ) > δ ||shift||=\sqrt{(1.5^2+(0.5)^2)}>\delta ∣∣shift∣∣=(1.52+(0.5)2)>δ,所以再次以 R = 5 R=5 R=5 为半径,圈定大佬的势力范围。在范围内的点 P4、P5、P6 即为该大佬的小弟。大佬为了笼络小弟们的心,给范围内的小弟人手一张保命卡。此时所有数据点的保命符情况:
| 保命符 | P1 | P2 | P3 | P4 | P5 | P6 |
|---|---|---|---|---|---|---|
| 大佬2 | 0 | 0 | 0 | 1 | 2 | 2 |
- 第二届选举大会:
首先,计算各位小弟到该大佬的向量距离(黑色向量)的平均值 s h i f t shift shift
| P4 | P5 | P6 | |
|---|---|---|---|
| 距离向量 | ( − 1.5 , − 0.5 ) (-1.5,-0.5) (−1.5,−0.5) | ( − 0.5 , 1.5 ) (-0.5,1.5) (−0.5,1.5) | ( 0.5 , − 1.5 ) (0.5,-1.5) (0.5,−1.5) |
则, s h i f t = ( − 1.5 − 0.5 + 0.5 3 , − 0.5 + 1.5 − 1.5 3 ) = ( − 0.5 , − 0.5 / 3 ) shift=(\dfrac{-1.5-0.5+0.5}{3}, \dfrac{-0.5+1.5-1.5}{3})=(-0.5,-0.5/3) shift=(3−1.5−0.5+0.5,3−0.5+1.5−1.5)=(−0.5,−0.5/3)
同样的方法选出新的虚拟大佬:P哥 ( 9.5 , 8.5 ) + ( − 0.5 , − 0.5 / 3 ) = ( 9 , 25 / 3 ) (9.5, 8.5)+(-0.5, -0.5/3) = (9, 25/3) (9.5,8.5)+(−0.5,−0.5/3)=(9,25/3)。
-
由于上一步偏移距离 ∣ ∣ s h i f t ∣ ∣ = ( ( 0.5 ) 2 + ( − 0.5 / 3 ) 2 ) < δ ||shift||=\sqrt{((0.5)^2+(-0.5/3)^2)}<\delta ∣∣shift∣∣=((0.5)2+(−0.5/3)2)<δ,当前的大佬 P 哥终于晋级为候选大佬了。
-
令超参 ω = 3 \omega=3 ω=3,比较候选大佬 P 哥跟所有正式大佬的距离。
目前正式大佬有一个 (5/3, 1),由于他们的距离大于阈值 ω \omega ω。P哥晋级为正式大佬了,晋级之路结束。此时,所有数据点的保命符情况:
| 保命符 | P1 | P2 | P3 | P4 | P5 | P6 |
|---|---|---|---|---|---|---|
| 大佬2 | 0 | 0 | 0 | 1 | 2 | 2 |
- 小弟们就要选择投靠哪位大佬了。此时,比较各位正式大佬在晋级路上给想所有数据点发的保命符情况:
| 保命符 | P1 | P2 | P3 | P4 | P5 | P6 |
|---|---|---|---|---|---|---|
| 大佬1 (4/3, 1) | 2 | 1 | 2 | 0 | 0 | 0 |
| 大佬2 (9, 25/3) | 0 | 0 | 0 | 1 | 2 | 2 |
小弟们选择投靠给自己保命卡最多的大佬,即
大佬1:P1、P2、P3
大佬2:P4、P5、P6
注意:假设第二个候选大佬 (9, 25/3) 跟正式大佬 (5/3, 1) 的距离小于阈值时,比如超参 ω = 20 \omega=20 ω=20,则当前候选大佬晋级失败,它发放的保命卡会被合并到该正式大佬中去,即:
| 保命符 | P1 | P2 | P3 | P4 | P5 | P6 |
|---|---|---|---|---|---|---|
| 大佬1 | 2 | 1 | 2 | 1 | 2 | 2 |
MeanShift聚类简易应用示例
关于 MeanShift 算法的具体代码,网上有各种版本,这里就不赘述了,下面结合 python 中的一些函数给出一个较为简洁的版本:
>>> from sklearn.cluster import MeanShift
>>> import numpy as np
>>> X = np.array([[0, 0], [1, 2], [3, 1],
[8, 8], [9, 10], [10, 7]])
>>> clustering = MeanShift(bandwidth=5).fit(X)
>>> clustering.predict([[0, 0], [1, 2], [3, 1],
[8, 8], [9, 10], [10, 7]])
>>> print(clustering.cluster_centers_)
array([[9. , 8.33333333],
[1.33333333, 1. ]])
可以看到,计算结果与手工推导一致。
总结
总而言之,投票时,KMeans中的小弟比较懒,投票的标准是:离哪位大佬近就投给谁。新大佬的位置即为小弟们坐标的加和平均;
MeanShift: 小弟是墙头草,投票的标准是:哪里的小弟多就往哪边投。新大佬的位置为旧大佬沿着小弟们投票出来的方向和距离漂移得到;
| 投票方式 | 更新方式 | |
|---|---|---|
| KMeans | 离谁近投给谁 | 小弟坐标平均均值 |
| MeanShift | 哪里人多往哪边投 | 沿平均方向偏移 |
拓展阅读
该部分只对 MeanShift 算法的拓展进行记录,不会深究,感兴趣的可以去查找相关资料。
- 核函数:在计算漂移向量的过程中,势力范围内小弟的贡献都是一样的。按照近朱者赤近墨者黑的原则,离中心点越近的小弟的影响力就会越大。因此就有人提出范围内的点需要设置不同的权重来作用于漂移向量的计算,故提出了核函数的概念。比较常见的有高斯核。
- 图像追踪:跟踪就是让第K帧的检测框移动到K+1帧对应位置上,这时候就需要指明移动的方向及位移,即mean shift算法中的漂移向量。
今天的文章聚类 之 MeanShift分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/13335.html