DEA各种模型原理及stata代码实现
DEA各种模型原理及stata代码实现
一、CCR和BCC
1.原理
CCR模型产出导向下的效率通过求解以下规划得出:
C C R _ T E = m a x θ CCR\_ TE = max \theta CCR_TE=maxθ
s . t . ∑ k = 1 K z k y k m ≥ y k m θ m , m = 1 , . . . , M s.t. \sum_{k=1}^Kz_{k}y_{km}\geq y_{km}\theta_{m},m=1,…,M s.t.∑k=1Kzkykm≥ykmθm,m=1,...,M
∑ k = 1 K z k x k n ≤ x k n , , n = 1 , . . . , N \kern2em\sum_{k=1}^Kz_{k}x_{kn}\leq x_{kn},,n=1,…,N ∑k=1Kzkxkn≤xkn,,n=1,...,N
z k ≥ 0 \kern2emz_{k}\geq 0 zk≥0
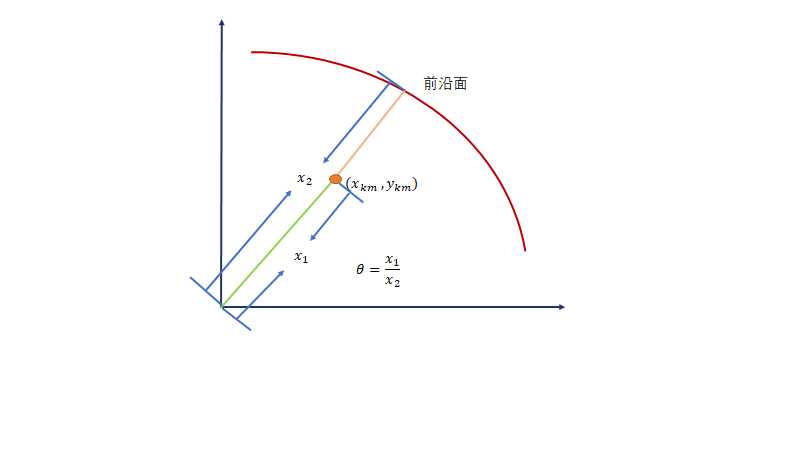
其中, ( ∑ k = 1 K z k y k m , ∑ k = 1 K z k x k n ) (\sum_{k=1}^Kz_{k}y_{km},\sum_{k=1}^Kz_{k}x_{kn}) (∑k=1Kzkykm,∑k=1Kzkxkn)可以理解为前沿面, ( x k m , y k m ) (x_{km},y_{km}) (xkm,ykm)为每个决策单元(dmu)的值。
BCC模型在上述规划的约束条件中加入 ∑ k = 1 K z k = 1 \sum_{k=1}^Kz_k=1 ∑k=1Kzk=1.
2.效率测算stata代码
代码格式如下:
CCR模型对应规模报酬不变crs
dea inputvars = outputvars ,rts(crs)
BCC模型对应规模报酬可变vrs
dea inputvars = outputvars ,rts(vrs)
3.Malmquist指数
3.1M指数
Malmquist指数是效率的变化率,简单地想,如果以t期为基期,那么公式为:
M a l m q u i s t t = D t ( x t + 1 , y t + 1 ) D t ( x t , y t ) Malmquist_t=\dfrac{D^t (x^{t+1},y^{t+1})}{D^t(x^t,y^t)} Malmquistt=Dt(xt,yt)Dt(xt+1,yt+1)
其中, D t ( x t + 1 , y t + 1 ) D^t(x^{t+1},y^{t+1}) Dt(xt+1,yt+1)某一个决策单元在t+1期的生产情况基于t期的前沿面计算的效率(决策单元在t+1期的生产情况可能超出t期的前沿面,因此可能无解);
D t ( x t , y t ) D^{t}(x^{t},y^{t}) Dt(xt,yt)某一个决策单元在t期的生产情况基于t期的前沿面计算的效率,也就是正常来说的 T E t TE_t TEt
同样的,如果以t+1期为基期,那么公式为:
M a l m q u i s t t + 1 = D t + 1 ( x t + 1 , y t + 1 ) D t + 1 ( x t , y t ) Malmquist_{t+1} =\dfrac{D^{t+1}(x^{t+1},y^{t+1})}{D^{t+1}(x^t,y^t)} Malmquistt+1=Dt+1(xt,yt)Dt+1(xt+1,yt+1)
基期不同值不同,为了解决这个问题,定义:
M a l m q u i s t t + 1 , t = ( M a l m q u i s t t × M a l m q u i s t t + 1 ) 0.5 = M ( x t + 1 , y t + 1 , x t , y t ) Malmquist_{t+1,t} =(Malmquist_{t}\times Malmquist_{t+1})^{0.5} =M(x^{t+1},y^{t+1},x^t,y^t) Malmquistt+1,t=(Malmquistt×Malmquistt+1)0.5=M(xt+1,yt+1,xt,yt)
= [ D t ( x t + 1 , y t + 1 ) D t ( x t , y t ) × D t + 1 ( x t + 1 , y t + 1 ) D t + 1 ( x t , y t ) ] 0.5 =[\dfrac{D^{t}(x^{t+1},y^{t+1})}{D^t(x^t,y^t)}\times \dfrac{D^{t+1}(x^{t+1},y^{t+1})}{D^{t+1}(x^t,y^t)}]^{0.5} =[Dt(xt,yt)Dt(xt+1,yt+1)×Dt+1(xt,yt)Dt+1(xt+1,yt+1)]0.5
= D t + 1 ( x t + 1 , y t + 1 ) D t ( x t , y t ) × [ D t ( x t + 1 , y t + 1 ) D t + 1 ( x t + 1 , y t + 1 ) D t ( x t , y t ) D t + 1 ( x t , y t ) ] 0.5 =\dfrac{D^{t+1}(x^{t+1},y^{t+1})}{D^t(x^t,y^t)}\times [\dfrac{D^{t}(x^{t+1},y^{t+1})}{D^{t+1}(x^{t+1},y^{t+1})}\dfrac{D^{t}(x^{t},y^{t})}{D^{t+1}(x^t,y^t)}]^{0.5} =Dt(xt,yt)Dt+1(xt+1,yt+1)×[Dt+1(xt+1,yt+1)Dt(xt+1,yt+1)Dt+1(xt,yt)Dt(xt,yt)]0.5
= T E C H × T E C C H =TECH \times TECCH =TECH×TECCH ——- Fare分解
其中:TECH表示效率变化,TECCH表示技术进步.
在规模报酬不变时,Fare分解完全正确,但是在规模报酬可变时,须考虑规模报酬的变化
T F P C H = M ( x t + 1 , y t + 1 , x t , y t ) TFPCH= M(x^{t+1},y^{t+1},x^t,y^t) TFPCH=M(xt+1,yt+1,xt,yt)
= D v t + 1 ( x t + 1 , y t + 1 ) D v t ( x t , y t ) × [ D c t ( x t + 1 , y t + 1 ) D t + 1 ( x t + 1 , y t + 1 ) D t ( x t , y t ) D t + 1 ( x t , y t ) ] 0.5 × D c t + 1 ( x t + 1 , y t + 1 ) / D v t + 1 ( x t + 1 , y t + 1 ) D c t ( x t , y t ) / D v t + 1 ( x t , y t ) =\dfrac{D^{t+1}_v(x^{t+1},y^{t+1})}{D^t_v(x^t,y^t)}\times [\dfrac{D^{t}_c(x^{t+1},y^{t+1})}{D^{t+1}(x^{t+1},y^{t+1})}\dfrac{D^{t}(x^{t},y^{t})}{D^{t+1}(x^t,y^t)}]^{0.5}\times \dfrac{D^{t+1}_c(x^{t+1},y^{t+1})/D^{t+1}_v(x^{t+1},y^{t+1})}{D^{t}_c(x^{t},y^{t})/D^{t+1}_v(x^{t},y^{t})} =Dvt(xt,yt)Dvt+1(xt+1,yt+1)×[Dt+1(xt+1,yt+1)Dct(xt+1,yt+1)Dt+1(xt,yt)Dt(xt,yt)]0.5×Dct(xt,yt)/Dvt+1(xt,yt)Dct+1(xt+1,yt+1)/Dvt+1(xt+1,yt+1)
= T E C H × T E C C H × S E C H =TECH \times TECCH \times SECH =TECH×TECCH×SECH ———–RD分解
其中, D c D_c Dc表示按规模报酬不变计算效率, D v D_v Dv表示按规模报酬可变计算效率,SECH表示规模变化。
3.2Global-Malmquist指数
Malmquist指数可能无解!
因此有Global Malaquist指数,思想很简单,计算一个全局效率,以他为基准,公式为:
G M = M c G ( x t , y t , x t + 1 , y t + 1 ) = D c G ( x t + 1 , y t + 1 ) D c G ( x t , y t ) GM = M^G_c(x^t,y^t,x^{t+1},y^{t+1})=\dfrac{D^G_c(x^{t+1},y^{t+1})}{D^G_c(x^t,y^t)} GM=McG(xt,yt,xt+1,yt+1)=DcG(xt,yt)DcG(xt+1,yt+1)
其中, D G D^G DG表示基于全局前沿面的效率。 D t D^t Dt的计算方式是仅保留第t期的数据来计算效率,而 D G D^G DG是将所有数据都保留来计算效率(不会无解)。
M c G ( x t , y t , x t + 1 , y t + 1 ) M^G_c(x^t,y^t,x^{t+1},y^{t+1}) McG(xt,yt,xt+1,yt+1)
= D c t + 1 ( x t + 1 , y t + 1 ) D c t ( x t , y t ) × D c G ( x t + 1 , y t + 1 ) D t + 1 ( x t + 1 , y t + 1 ) D c t ( x t , y t ) D G ( x t , y t ) =\dfrac{D^{t+1}_c(x^{t+1},y^{t+1})}{D^t_c(x^t,y^t)}\times \dfrac{D^{G}_c(x^{t+1},y^{t+1})}{D^{t+1}(x^{t+1},y^{t+1})}\dfrac{D^{t}_c(x^{t},y^{t})}{D^{G}(x^t,y^t)} =Dct(xt,yt)Dct+1(xt+1,yt+1)×Dt+1(xt+1,yt+1)DcG(xt+1,yt+1)DG(xt,yt)Dct(xt,yt)
= T E C H × B P C =TECH\times BPC =TECH×BPC
其中,TECH 是通常的效率变化指标,BPG 是最佳实践差距,表明t+1期的基准技术相较于t期是接近还是远离了全局的基准⽣产技 术。当然也可以采用RD分解,分解规模变化。
4.指数计算代码与案例
malmq2 inputvars = outputvars ,
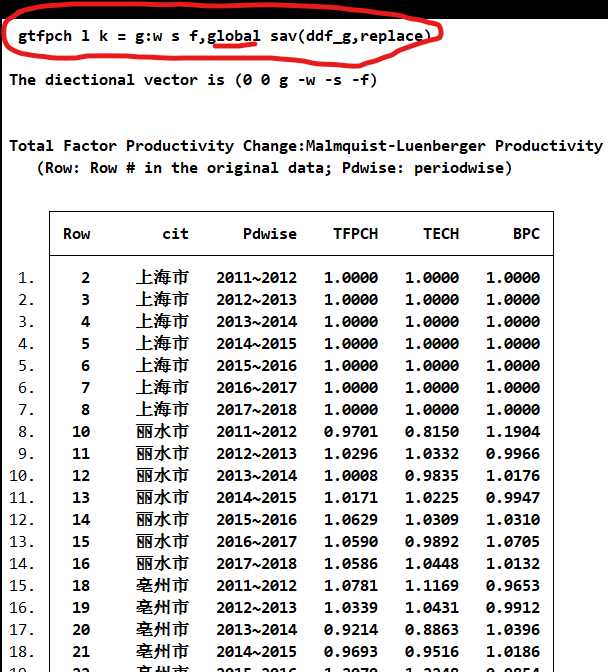
选项:global 计算Golbal-Malmquist指数
saving() 保存
案例数据展示,其中投入为l和k,期望产出为g,非期望产出为w,s,f
| year | city | w | s | f | l | g | k |
|---|---|---|---|---|---|---|---|
| 2018 | 上海市 | 29144 | 9100 | 16163 | 1375.66 | 31521.2 | 7.60E+07 |
| 2018 | 南京市 | 15534 | 12375 | 35914 | 462.6 | 11752.8 | 7.00E+07 |
| 2018 | 无锡市 | 20622 | 40242 | 52929 | 388.2 | 11897 | 5.10E+07 |
先设置面板xtset
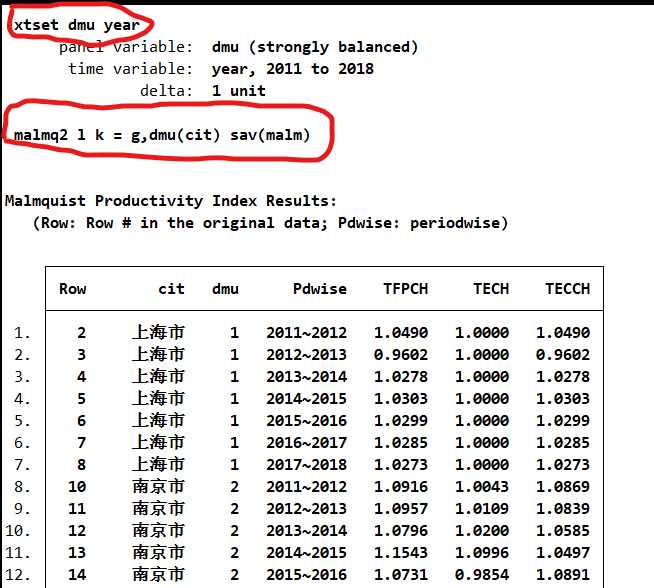
然后计算malmquist指数(l k为投入,g为产出),fare分解
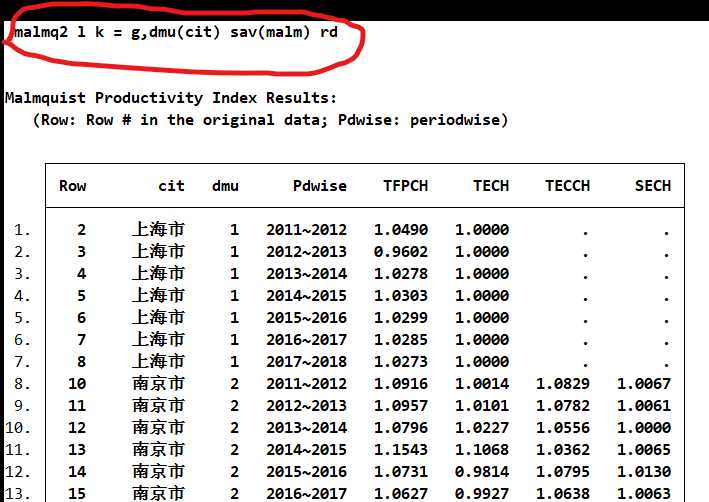
RD分解:
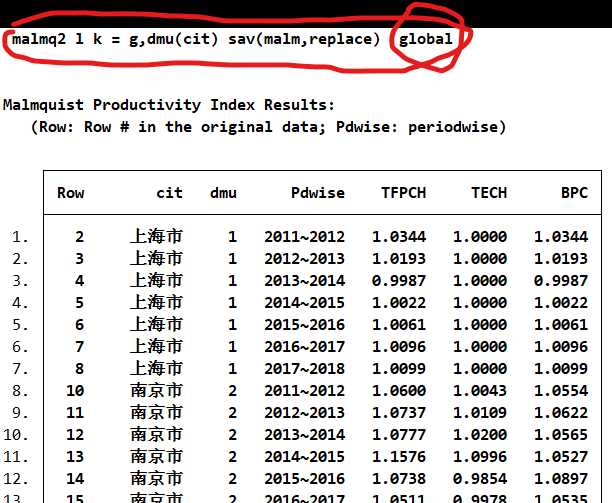
GM指数计算
二、SBM模型
1.原理
带有非期望产出的SBM模型:
p h i ∗ = m i n 1 − 1 m ∑ i = 1 m ( S i o − X i o ) 1 + 1 s 1 + s 2 ( ∑ r 1 = 1 s 1 S r 1 o g y r 1 o g + ∑ r 2 = 1 s 2 S r 2 o b y r 2 o b ) phi^*=min\dfrac{1 – \dfrac{1}{m} \sum_{i=1}^m(\dfrac{S_{io}^-}{X_{io}})}{1+\dfrac{1}{s_1+s_2}(\sum_{r_1=1}^{s_1}\dfrac{S_{r_{1o}}^g}{y_{r_{1o}}^g}+\sum_{r_2=1}^{s_2}\dfrac{S_{r_{2o}}^b}{y_{r_{2o}}^b})} phi∗=min1+s1+s21(∑r1=1s1yr1ogSr1og+∑r2=1s2yr2obSr2ob)1−m1∑i=1m(XioSio−)
s . t X o = X λ + S o − ( 1 ) s.t\kern5em X_o=X\lambda +S_o^- \kern3em(1) s.tXo=Xλ+So−(1)
y o g = Y g λ − S o g ( 2 ) \kern6em y_o^g=Y^g\lambda -S_o^g \kern3em(2) yog=Ygλ−Sog(2)
y o b = Y b λ + S o b ( 3 ) \kern6em y_o^b = Y^b\lambda + S_o^b \kern3em(3) yob=Ybλ+Sob(3)
S o − , S o g , S o b , λ > 0 ( 4 ) \kern6em S_o^-,S_o^g,S_o^b, \lambda >0 \kern2em(4) So−,Sog,Sob,λ>0(4)
其中, ( X o , y o g , y o b ) (X_o,y^g_o,y^b_o) (Xo,yog,yob)分别表示每个决策单元的值, ( X λ , y g λ , y b λ ) (X\lambda,y^g\lambda,y^b\lambda) (Xλ,ygλ,ybλ)表示前沿面。
S o − , S o g , S o b S_o^-,S_o^g,S_o^b So−,Sog,Sob表示松弛值,即投入或产出与前沿面的距离,也即投入比理想投入多的部分、期望产出比理想期望产出少的部分、非期望产出比理想非期望产出多的部分。 ϕ ∗ \phi^* ϕ∗即得出的效率。
2.stata代码实现
无非期望产出
sbmeff inputvars = desirable_outputvars , dmu(varname)
有非期望产出
sbmeff inputvars = desirable_outputvars : undesirable_outputvars , dmu(varname)
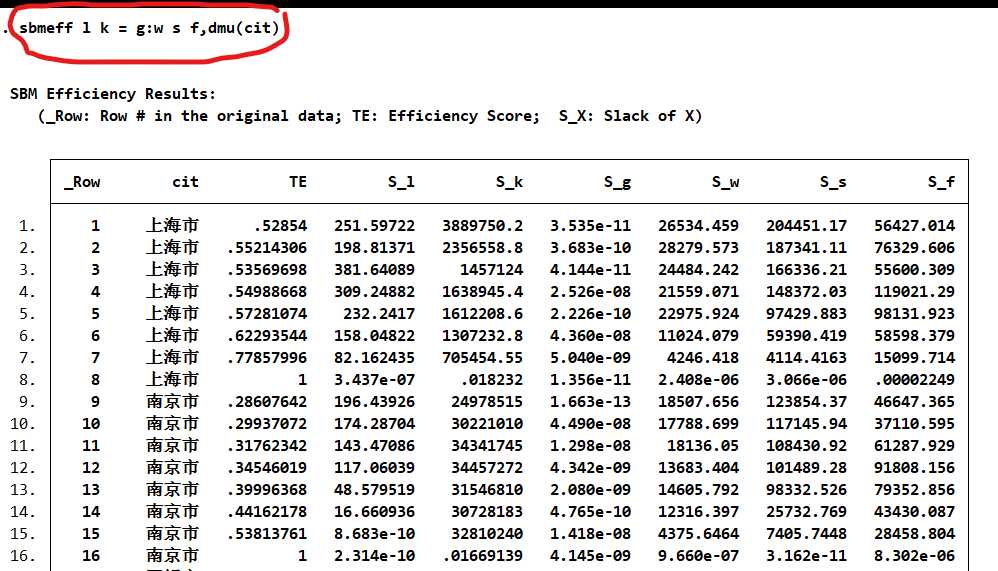
TE表示效率
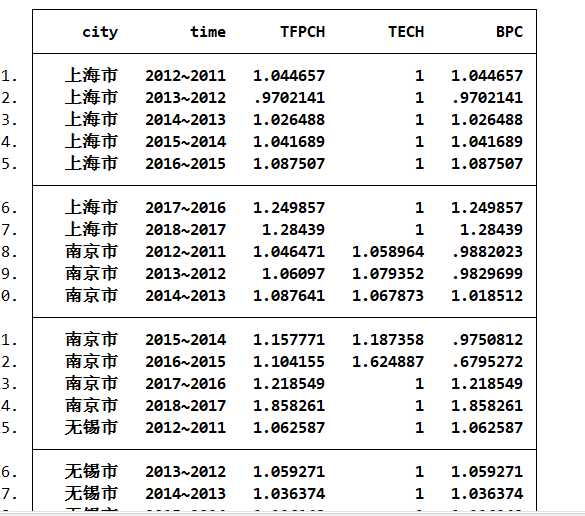
指数计算
** sbm_t
sbmeff l k = g:w s f,dmu(cit) time(year) sav(sbm_t,replace)
** sbm_g 全局前沿
sbmeff l k = g:w s f,dmu(cit) sav(sbm_g,replace)
merge m:m cit using sbm_g
rename TE TE_G
drop _merge
merge 1:1 cit year using sbm_t
drop _merge
xtset dmu year
tostring year, generate(time1)
gen lyear = l.year
tostring lyear, generate(time2)
gen time = time1 + "~" +time2
gen TFPCH = TE_G / l.TE_G
gen TECH = TE/l.TE
gen BPC = TFPCH / TECH
keep if TFPCH != .
list city time TFPCH TECH BPC
三、方向性距离函数(DDF)
1.原理
D → ( x , y , b ; g ) = m a x β \overrightarrow{D}(x,y,b;g)=max\beta D(x,y,b;g)=maxβ
s . t . ∑ n = 1 N z n x m n ≤ x m − β g x m , m = 1 , 2… , M s.t. \sum_{n=1}^Nz_nx_{mn} \leq x_m-\beta g_{xm},m=1,2…,M s.t.∑n=1Nznxmn≤xm−βgxm,m=1,2...,M
∑ n = 1 N z n y s n ≥ y s + β g y s , s = 1 , 2… , S \kern4ex\sum_{n=1}^Nz_ny_{sn} \geq y_s+\beta g_{ys},s=1,2…,S ∑n=1Nznysn≥ys+βgys,s=1,2...,S
∑ n = 1 N z n b j n = b j − β g b j , j = 1 , 2… , J \kern4ex\sum_{n=1}^Nz_nb_{jn} =b_j-\beta g_{bj},j=1,2…,J ∑n=1Nznbjn=bj−βgbj,j=1,2...,J
z n ≥ 0 , β > 0 , n = 1 , 2… , N \kern4ex z_n\geq 0 ,\beta>0,n=1,2…,N zn≥0,β>0,n=1,2...,N
其中, g g g为投⼊和产出的缩放的⽅向向量, β \beta β为无效率值。
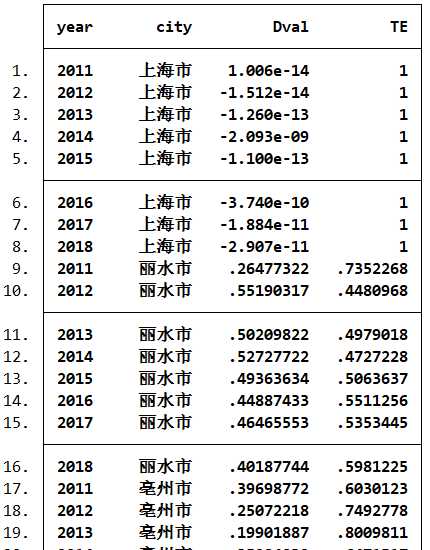
2.stata代码实现
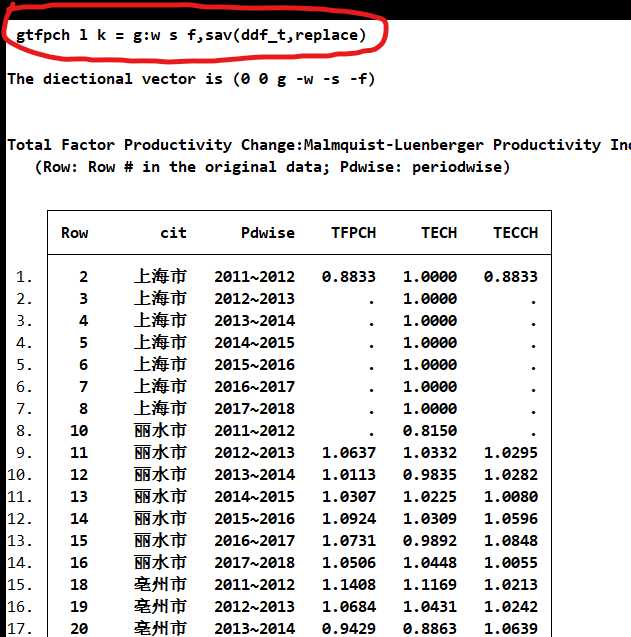
ddfeff l k = g:w s f,dmu(cit) time(year) sav(ddf,)
merge 1:1 cit year using ddf
gen TE = 1-Dval
list year city Dval TE
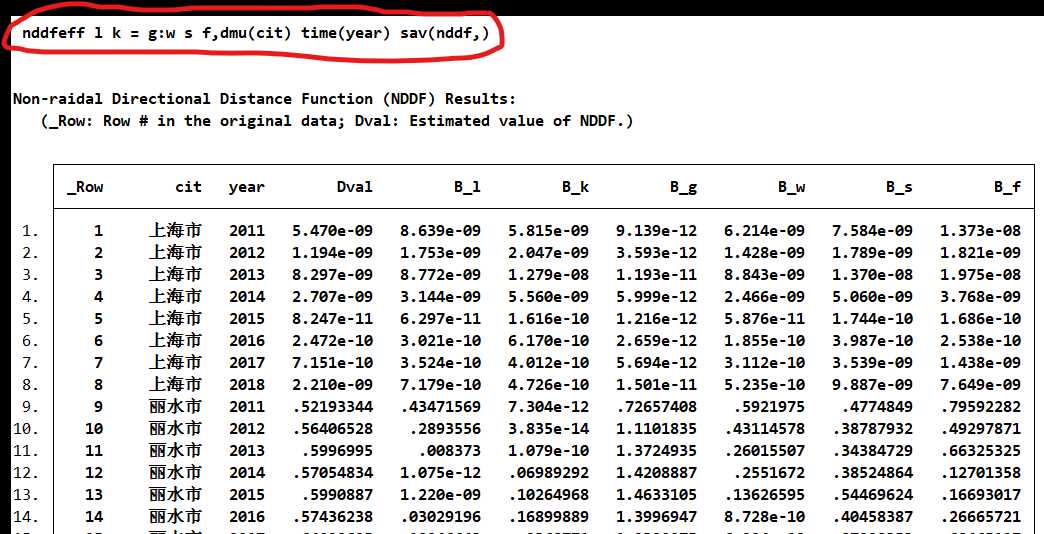
3.非径向DDF模型(NDDF)
N D → ( x , y , b ; g ) = m a x ( w m x β s y + w s t β s y + w j b β j b ) \overrightarrow{ND}(x,y,b;g)=max( w^x_m \beta_s^y+w_s^t\beta^y_s+w_j^b\beta_j^b) ND(x,y,b;g)=max(wmxβsy+wstβsy+wjbβjb)
s . t . ∑ n = 1 N z n x m n ≤ x m − β m s g x m , m = 1 , 2… , M s.t. \sum_{n=1}^Nz_nx_{mn} \leq x_m-\beta_m^s g_{xm},m=1,2…,M s.t.∑n=1Nznxmn≤xm−βmsgxm,m=1,2...,M
∑ n = 1 N z n y s n ≥ y s + β s y g y s , s = 1 , 2… , S \kern4ex\sum_{n=1}^Nz_ny_{sn} \geq y_s+\beta_s^y g_{ys},s=1,2…,S ∑n=1Nznysn≥ys+βsygys,s=1,2...,S
∑ n = 1 N z n b j n = b j − β j b g b j , j = 1 , 2… , J \kern4ex\sum_{n=1}^Nz_nb_{jn} =b_j-\beta_j^b g_{bj},j=1,2…,J ∑n=1Nznbjn=bj−βjbgbj,j=1,2...,J
z n ≥ 0 , β > 0 , n = 1 , 2… , N \kern4ex z_n\geq 0 ,\beta>0,n=1,2…,N zn≥0,β>0,n=1,2...,N
NDDF模型对比DDF只是让投入产出的无效率系数变为不同。
NDDF模型代码实现
由于结果给出了所有方向的 β \beta β,也可以按照自己的方法计算TE(自己定义的公式).比如:
T E = 1 − 0.2 ( B _ l + B _ k + B _ w + B _ s + B _ f ) 1 + B g TE=\dfrac{1-0.2(B\_l +B\_k+B\_w+B\_s+B\_f)}{1+B_g} TE=1+Bg1−0.2(B_l+B_k+B_w+B_s+B_f)
其内涵为每种因素的平均效率。
3.GML指数
计算完效率之后可以计算效率的变化率Global-Malmquist-Luenberger指数。
由于已被证明:
D → ( x , y , b ; g ) = 1 1 + D ( x , y , b ) \overrightarrow{D}(x,y,b;g)=\dfrac{1}{1+D(x,y,b)} D(x,y,b;g)=1+D(x,y,b)1
因此有Malmquist-Luenberger指数:
M L = D t ( x t + 1 , y t + 1 , b t + 1 ; g t + 1 ) × D t + 1 ( x t + 1 , y t + 1 , b t + 1 ; g t + 1 ) D t ( x t , y t , b t ; g t ) × D t + 1 ( x t , y t , b t ; g t ) ML=\dfrac{
{D^t}(x^{t+1},y^{t+1},b^{t+1};g^{t+1})\times{D^{t+1}}(x^{t+1},y^{t+1},b^{t+1};g^{t+1})}{
{D^t}(x^t,y^t,b^t;g^t)\times{D^{t+1}}(x^{t},y^t,b^t;g^t)} ML=Dt(xt,yt,bt;gt)×Dt+1(xt,yt,bt;gt)Dt(xt+1,yt+1,bt+1;gt+1)×Dt+1(xt+1,yt+1,bt+1;gt+1)
= [ 1 + D t → ( x t , y t , b t ) 1 + D t → ( x t + 1 , y t + 1 , b t + 1 ) × 1 + D t + 1 → ( x t , y t , b t ) 1 + D t + 1 → ( x t + 1 , y t + 1 , b t + 1 ) ] 0.5 \kern4ex =[\dfrac{1 + \overrightarrow{D^t}(x^t,y^t,b^t)}{1+\overrightarrow{D^{t}}(x^{t+1},y^{t+1},b^{t+1})}\times \dfrac{1+ \overrightarrow{D^{t+1}}(x^t,y^t,b^t)}{1+\overrightarrow{D^{t+1}}(x^{t+1},y^{t+1},b^{t+1})}]^{0.5} =[1+Dt(xt+1,yt+1,bt+1)1+Dt(xt,yt,bt)×1+Dt+1(xt+1,yt+1,bt+1)1+Dt+1(xt,yt,bt)]0.5
和GML指数
G M L = D G ( x t + 1 , y t + 1 , b t + 1 ) D G ( x t , y t , b t ) = 1 + D G → ( x t , y t , b t ) 1 + D G → ( x t + 1 , y t + 1 , b t + 1 ) GML = \dfrac{D^G(x^{t+1},y^{t+1},b^{t+1})}{D^G(x^t,y^t,b^t)} = \dfrac{1+\overrightarrow{D^G}(x^{t},y^{t},b^{t})}{1+\overrightarrow{D^G}(x^{t+1},y^{t+1},b^{t+1})} GML=DG(xt,yt,bt)DG(xt+1,yt+1,bt+1)=1+DG(xt+1,yt+1,bt+1)1+DG(xt,yt,bt)
= 1 + D t → ( x t , y t , b t ) 1 + D + 1 → ( x t + 1 , y t + 1 , b t + 1 ) × ( 1 + D G → ( x t , y t , b t ) ) / ( 1 + D t → ( x t , y t , b t ) ) ( 1 + D G → ( x t + 1 , y t + 1 , b t + 1 ) ) / ( 1 + D + 1 → ( x t + 1 , y t + 1 , b t + 1 ) ) \kern5ex = \dfrac{1+\overrightarrow{D^t}(x^{t},y^{t},b^{t})}{1+\overrightarrow{D^+1}(x^{t+1},y^{t+1},b^{t+1})} \times \dfrac{(1+\overrightarrow{D^G}(x^{t},y^{t},b^{t}) )/(1+\overrightarrow{D^t}(x^{t},y^{t},b^{t}))}{(1+\overrightarrow{D^G}(x^{t+1},y^{t+1},b^{t+1}))/ (1+\overrightarrow{D^+1}(x^{t+1},y^{t+1},b^{t+1}))} =1+D+1(xt+1,yt+1,bt+1)1+Dt(xt,yt,bt)×(1+DG(xt+1,yt+1,bt+1))/(1+D+1(xt+1,yt+1,bt+1))(1+DG(xt,yt,bt))/(1+Dt(xt,yt,bt))
= T E C H × B P C \kern5ex = TECH \times BPC =TECH×BPC
4.指数测算
ML指数
存在大量缺失值,使用gml指数
四、总结
上述包含了 dea、malmq2、ddfeff等命令,可能需要高版本stata,stata16最好。如果缺少了命令,可通过 ssc install XX (XX为命令名称)下载,网络不好可能下载失败。也可使用其他人下载好的命令,推荐 连玉君老师的plus文件。
文中相关数据和资源:
链接:https://pan.baidu.com/s/15wMpDovYiqG-LI74Z_NhPQ
提取码:em4g
最后,在肝论文的小伙伴,都帮你们到这了,不点个大大的赞吗!!
今天的文章DEA各种模型原理及stata代码实现分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/13367.html