一、VRP简介
1 VRP基本原理 车辆路径规划问题(Vehicle Routing Problem,VRP)是运筹学里重要的研究问题之一。VRP关注有一个供货商与K个销售点的路径规划的情况,可以简述为:对一系列发货点和收货点,组织调用一定的车辆,安排适当的行车路线,使车辆有序地通过它们,在满足指定的约束条件下(例如:货物的需求量与发货量,交发货时间,车辆容量限制,行驶里程限制,行驶时间限制等),力争实现一定的目标(如车辆空驶总里程最短,运输总费用最低,车辆按一定时间到达,使用的车辆数最小等)。 VRP的图例如下所示: 
3 常见问题有以下几类: (1)旅行商问题 (2)带容量约束的车辆路线问题(CVRP) 













4 解决方案 (1)数学解析法 (2)人机交互法 (3)先分组再排路线法 (4)先排路线再分组法 (5)节省或插入法 (6)改善或交换法 (7)数学规划近似法 (8)启发式算法
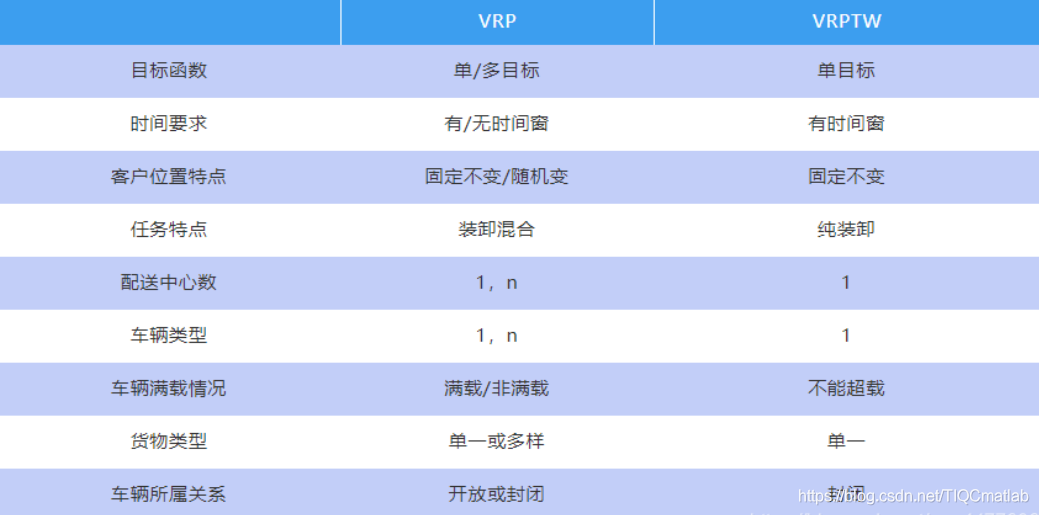
5 VRP与VRPTW对比
二、遗传算法简介
1 引言 




















三、部分源代码
clear
clc
close all
tic
%% 读取数据
load('shuju7');
bl=0;
%% 提取数据信息
E=shuju(1,4); %初始点时间窗开始时间
L=shuju(1,5); %初始点心时间窗结束时间
zuobiao=shuju(:,2:3); %所有点的坐标x和y
zuobiao=[zuobiao(:,1),-zuobiao(:,2)];
customer=zuobiao(2:end,:); %顾客坐标
cusnum=size(customer,1); %顾客数
v_num=1; %车辆数
a=shuju(2:end,4); %顾客时间窗开始时间[a[i],b[i]]
b=shuju(2:end,5); %顾客时间窗结束时间[a[i],b[i]]
F=shuju(2:end,1);
dist=load('shiji7.mat');%D导入距离矩阵
dist=struct2cell(dist);
dist=cell2mat(dist);
%% 遗传算法参数设置
chesu=300;%车速
alpha=100000; %违反的容量约束的惩罚函数系数
belta=chesu/1000;%违反时间窗约束的惩罚函数系数
belta2=1;
NIND=1000; %种群大小
MAXGEN=50; %迭代次数
Pc=0.9; %交叉概率
Pm=0.05; %变异概率
GGAP=0.9; %代沟(Generation gap)
N=cusnum;
%% 初始化种群
[s,g,sj,gk,Chrom]=init(cusnum,NIND,F); %构造初始解
%% 输出随机解的路线和总距离
disp('初始种群中的一个随机值:')
[VC,TD,violate_cus]=decode(Chrom(1,:),cusnum,a,b,L,dist,chesu,bl);
% disp(['总距离:',num2str(TD)]);
disp(['车辆行驶总距离:',num2str(TD)]);
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
%% 优化
function lineStyles=linspecer(N,varargin)
if nargin==0 % return a colormap
lineStyles = linspecer(128);
return;
end
if ischar(N)
lineStyles = linspecer(128,N);
return;
end
if N<=0 % its empty, nothing else to do here
lineStyles=[];
return;
end
% interperet varagin
qualFlag = 0;
colorblindFlag = 0;
if ~isempty(varargin)>0 % you set a parameter?
switch lower(varargin{1})
case {'qualitative','qua'}
if N>12 % go home, you just can't get this.
warning('qualitiative is not possible for greater than 12 items, please reconsider');
else
if N>9
warning(['Default may be nicer for ' num2str(N) ' for clearer colors use: whitebg(''black''); ']);
end
end
qualFlag = 1;
case {'sequential','seq'}
lineStyles = colorm(N);
return;
case {'white','whitefade'}
lineStyles = whiteFade(N);return;
case 'red'
lineStyles = whiteFade(N,'red');return;
case 'blue'
lineStyles = whiteFade(N,'blue');return;
case 'green'
lineStyles = whiteFade(N,'green');return;
case {'gray','grey'}
lineStyles = whiteFade(N,'gray');return;
case {'colorblind'}
colorblindFlag = 1;
otherwise
warning(['parameter ''' varargin{1} ''' not recognized']);
end
end
% *.95
% predefine some colormaps
set3 = colorBrew2mat({[141, 211, 199];[ 255, 237, 111];[ 190, 186, 218];[ 251, 128, 114];[ 128, 177, 211];[ 253, 180, 98];[ 179, 222, 105];[ 188, 128, 189];[ 217, 217, 217];[ 204, 235, 197];[ 252, 205, 229];[ 255, 255, 179]}'); set1JL = brighten(colorBrew2mat({[228, 26, 28];[ 55, 126, 184]; [ 77, 175, 74];[ 255, 127, 0];[ 255, 237, 111]*.85;[ 166, 86, 40];[ 247, 129, 191];[ 153, 153, 153];[ 152, 78, 163]}'));
set1 = brighten(colorBrew2mat({[ 55, 126, 184]*.85;[228, 26, 28];[ 77, 175, 74];[ 255, 127, 0];[ 152, 78, 163]}),.8);
% colorblindSet = {[215,25,28];[253,174,97];[171,217,233];[44,123,182]};
colorblindSet = {[215,25,28];[253,174,97];[171,217,233]*.8;[44,123,182]*.8};
set3 = dim(set3,.93);
if colorblindFlag
switch N
% sorry about this line folks. kind of legacy here because I used to
% use individual 1x3 cells instead of nx3 arrays
case 4
lineStyles = colorBrew2mat(colorblindSet);
otherwise
colorblindFlag = false;
warning('sorry unsupported colorblind set for this number, using regular types');
end
end
if ~colorblindFlag
switch N
case 1
lineStyles = { [ 55, 126, 184]/255};
case {2, 3, 4, 5 }
lineStyles = set1(1:N);
case {6 , 7, 8, 9}
lineStyles = set1JL(1:N)'; case {10, 11, 12} if qualFlag % force qualitative graphs lineStyles = set3(1:N)';
else % 10 is a good number to start with the sequential ones.
lineStyles = cmap2linspecer(colorm(N));
end
otherwise % any old case where I need a quick job done.
lineStyles = cmap2linspecer(colorm(N));
end
end
lineStyles = cell2mat(lineStyles);
end
% extra functions
function varIn = colorBrew2mat(varIn)
for ii=1:length(varIn) % just divide by 255
varIn{ii}=varIn{ii}/255;
end
end
function varIn = brighten(varIn,varargin) % increase the brightness
if isempty(varargin),
frac = .9;
else
frac = varargin{1};
end
for ii=1:length(varIn)
varIn{ii}=varIn{ii}*frac+(1-frac);
end
end
function varIn = dim(varIn,f)
for ii=1:length(varIn)
varIn{ii} = f*varIn{ii};
end
end
function vOut = cmap2linspecer(vIn) % changes the format from a double array to a cell array with the right format
vOut = cell(size(vIn,1),1);
for ii=1:size(vIn,1)
vOut{ii} = vIn(ii,:);
end
end
%%
% colorm returns a colormap which is really good for creating informative
% heatmap style figures.
% No particular color stands out and it doesn't do too badly for colorblind people either.
% It works by interpolating the data from the
% 'spectral' setting on http://colorbrewer2.org/ set to 11 colors
% It is modified a little to make the brightest yellow a little less bright.
function cmap = colorm(varargin)
n = 100;
if ~isempty(varargin)
n = varargin{1};
end
if n==1
cmap = [0.2005 0.5593 0.7380];
return;
end
if n==2
cmap = [0.2005 0.5593 0.7380;
0.9684 0.4799 0.2723];
return;
end
frac=.95; % Slight modification from colorbrewer here to make the yellows in the center just a bit darker
cmapp = [158, 1, 66; 213, 62, 79; 244, 109, 67; 253, 174, 97; 254, 224, 139; 255*frac, 255*frac, 191*frac; 230, 245, 152; 171, 221, 164; 102, 194, 165; 50, 136, 189; 94, 79, 162];
x = linspace(1,n,size(cmapp,1));
xi = 1:n;
cmap = zeros(n,3);
for ii=1:3
cmap(:,ii) = pchip(x,cmapp(:,ii),xi);
end
cmap = flipud(cmap/255);
end
function cmap = whiteFade(varargin)
n = 100;
if nargin>0
n = varargin{1};
end
thisColor = 'blue';
if nargin>1
thisColor = varargin{2};
end
switch thisColor
case {'gray','grey'}
cmapp = [255,255,255;240,240,240;217,217,217;189,189,189;150,150,150;115,115,115;82,82,82;37,37,37;0,0,0];
case 'green'
cmapp = [247,252,245;229,245,224;199,233,192;161,217,155;116,196,118;65,171,93;35,139,69;0,109,44;0,68,27];
case 'blue'
cmapp = [247,251,255;222,235,247;198,219,239;158,202,225;107,174,214;66,146,198;33,113,181;8,81,156;8,48,107];
case 'red'
cmapp = [255,245,240;254,224,210;252,187,161;252,146,114;251,106,74;239,59,44;203,24,29;165,15,21;103,0,13];
otherwise
warning(['sorry your color argument ' thisColor ' was not recognized']);
end
cmap = interpomap(n,cmapp);
end
% Eat a approximate colormap, then interpolate the rest of it up.
function cmap = interpomap(n,cmapp)
x = linspace(1,n,size(cmapp,1));
xi = 1:n;
cmap = zeros(n,3);
for ii=1:3
cmap(:,ii) = pchip(x,cmapp(:,ii),xi);
end
cmap = (cmap/255); % flipud??
end
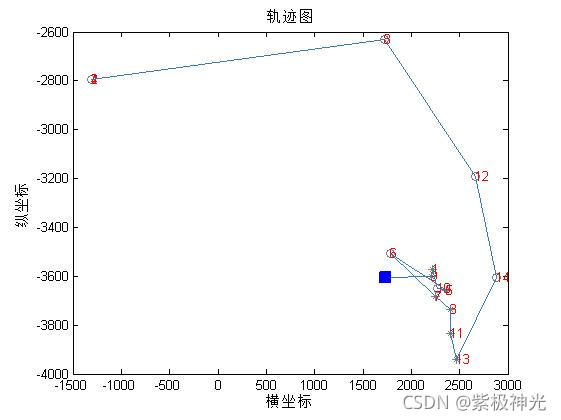
四、运行结果

五、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016. [2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
今天的文章【TWVRP】基于matlab遗传算法求解带时间窗的载重约束外卖配送车辆路径规划问题【含Matlab源码 1417期】分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/14864.html