【图像分割】基于snake模型实现图像分割含Matlab源码

1 简介

视觉是人类最重要的感知手段之一，同时视觉信息是人类从自然界中获得信

息的主要来源，约占人类获得外部世界信息量的 80%以上。图像以视觉为基础通过观测系统直接获得客观世界的状态，它直接或间接地作用于人眼，反映的信息与人眼获得的信息一致，这决定了它和客观外界都是人类最主要的信息来源，图像处理也因此成为了人们研究的热点之一。人眼获得的信息是连续的图像，在实际应用中，为便于计算机等对图像进行处理，人们对连续图像进行采样和量化等处理，得到了计算机能够识别的数字图像。数字图像具有信息量大、精度高、内容丰富、可进行复杂的非线性处理等优点，成为计算机视觉和图像处理的重要研究对象.

1987 年 M. Kass 等人提出的 Snake 模型将图像、目标边缘、初始轮廓曲线和约束条件统一起来，在整个图像域中定义与曲线形状相关的内部能量和与图像域相关的外部能量，同时在图像空间内部给定初始轮廓曲线，轮廓曲线在控制曲线光滑性和连续性的内部能量和促进曲线向目标边缘运动的外部能量的共同作用下不断形变，最终收敛到目标轮廓。该模型计算简单、效率高、易于建模、能提取任意形状且连续的目标边缘。因而，在图像分割、边缘检测和目标识别与跟踪等方面得到了广泛的应用。

传统的 Snake 模型以高斯势能力为外力，存在初始化轮廓曲线要求高，捕获范围小，不能收敛到深度的凹形边界，弱边缘易被淹没等缺陷。针对这些问题，研究者们提出了很多改进方法。如气球力活动轮廓模型[38](Balloon Snake)、距离势能力模型[39]、动态距离力模型[40]、梯度向量流活动轮廓模型[41](Gradient Vector FlowSnake, GVF Snake)等。

针对传统 Snake 模型中 Gaussian 势能力作用范围小，1991 年 L. Cohen 提出了气球 Snake 模型，该模型依据气球膨胀和收缩的物理特性引入的气球力(BalloonForce)与图像特征无关，轮廓曲线在图像任何区域都能受到该力的影响，由此模型的捕获范围扩大到整个图像。但是 Snake 曲线只能膨胀或收缩的物理特性，致使初始轮廓曲线必须完全置于目标边缘的内部或外部，因而，气球力并不是作为一个单独的力场对图像进行分割，而是与 Gaussian 势能力结合使用。这使得气球力的大小难以确定，该力过大，轮廓曲线会穿过目标边界；过小，则会停留在假边缘上。因此，该模型的实用性较差。

1993 年 L. D. Cohen 和 I. Cohen 分析气球力模型提出的距离势能力模型依据像素点到其最近的边缘之间的距离映射来建立能量函数，获得整幅图像域的力场，该模型不仅克服了气球力模型过度收敛造成边缘泄露的缺陷，还能对 3D 图像进行分割。但是该模型不能收敛凹形边缘。

1994 年 W. Neuenschwander 等人提出了动态距离力势能模型，该模型通过沿轮廓曲线法矢量方向最近的边界点来求取距离力，很好地解决了距离势能力模型不能收敛到深凹的问题，但是，在轮廓曲线的迭代过程中，距离力不断变化，增大了算法的计算量，且由于模型的捕获范围与效率之间成反比，限制了该算法的实用性。

Xu Chenyang等人于1998年提出了GVF Snake模型，该模型引入梯度向量场，通过扩散方程将图像的梯度信息扩散到平滑区，将传统 Snake 模型直接利用梯度的突变问题转化为一个扩散梯度的渐变问题，有效地扩大了轮廓曲线的捕获范围，降低了初始轮廓线的设置要求。该特性使其在实际中得到了广泛的应用。并且，GVF Snake 模型将 Snake 模型中能量最小化的求解转化为外力场和内部力之间的力平衡问题，在很大的程度上完善了 Snake 模型的理论知识。这一新理论使学者将 Snake 模型的研究重点转移到梯度向量流力场的改进与优化。

在 GVF Snake 模型被提出后，Xu Chenyang 等人[42]通过分析外力场在平滑区域和边缘区域的分布形势，对原有的梯度向量场进行改进，提出了 GGVFSnake(General GVF Snake)模型，该模型引入随空间变换的权重函数来控制力场在边缘区和平滑区的扩散速度，降低了梯度向量流在扩散过程中对边缘区域的影响，起到了保护边缘的作用，但是，该模型极易陷入局部极小，导致得到错误的分割结果。2005 年 Li Chunming 等[43]在 GGVF Snake 模型的基础上提出 EPGVFSnake(Edge Preserving GVF Snake)模型，该模型引入的边缘保护项将梯度向量场与整个图像域联系起来，促使外力场沿着边缘方向平滑而不相交，在防止曲线穿过弱边缘和保护图像细节方面取得了良好的效果，但是该模型仍存在易陷入局部极小的缺陷。2007 年宁纪锋等[44]提出的 NGVF Snake(Normalized GVF Snake)模型根据图像的局部特性将拉普拉斯扩散项分解为沿边缘切线方向和法线方向的扩散，分别分析这两个方向的扩散对外力场的影响，发现法线方向的扩散在整个梯度向量流扩散过程中起到主要作用，因而该模型只保留了法线方向的扩散力，提高了轮廓曲线的收敛效率，也能促使曲线进入细长的凹部，但是切线方向扩散力的缺失导致边缘缺口处的信息遗失，力场性能下降，造成边缘泄露，在边缘不连续处收敛速度慢，且存在对噪声敏感等缺陷。针对 NGVF Snake 模型由缺失切线方向扩散引起的缺陷，2010 年 Wang Yuanquan 等保留扩散力切线方向分量提出 NBGVFSnake[45](Normally Biased GVF Snake)模型，该模型将随图像域空间变化的权重函数引入到扩散方程中，降低法线方向的扩散对边缘区域的影响和提高在平滑区域的扩散速度，由此，不仅保留了切线方向扩散力的抗噪性能，而且还能检查到弱边缘，提高轮廓曲线的收敛速度，但对角点的定位效果较差。针对 GGVF Snake模型不能促使轮廓曲线进如细长的深凹内部，2013 年 Qin Lunming 等[46]对 GGVFSnake 模型在深凹内部的扩散形式进行分析，发现 GGVF Snake 模型中促进轮廓进去深凹内部的力场易被深凹口边缘的力场扩散淹没，由此，通过单独归一化每个初始 GGVF 矢量的各分量提出 CN-GGVF Snake (Component-normalized GGVFSnake)模型，该模型较 GGVF Snake 模型更容易地收敛深凹边缘，具有更大的捕获范围，抗噪性能也有明显的提高，但其边缘泄露现象严重，边缘细节易被破坏。

2 部分代码

% This Matlab file demomstrates the level set method in Li et al's paper%    "Level Set Evolution Without Re-initialization: A New Variational Formulation"%    in Proceedings of CVPR'05, vol. 1, pp. 430-436.% Author: Chunming Li, all rights reserved.% E-mail: li_chunming@hotmail.com% URL:  http://vuiis.vanderbilt.edu/~licm/​clear all;close all;Img = imread('twoObj.bmp');  % The same cell image in the paper is used hereImg=double(Img(:,:,1));sigma=1.5;    % scale parameter in Gaussian kernel for smoothingG=fspecial('gaussian',15,sigma);Img_smooth=conv2(Img,G,'same');  % smooth image by Gaussiin convolution[Ix,Iy]=gradient(Img_smooth);f=Ix.^2+Iy.^2;g=1./(1+f);  % edge indicator function.​epsilon=1.5; % the papramater in the definition of smoothed Dirac function​timestep=1;  % time stepmu=0.2/timestep;  % coefficient of the internal (penalizing) energy term P(\phi)          % Note: the product timestep*mu must be less than 0.25 for stability!​lambda=5; % coefficient of the weighted length term L(\phi)alf=3;  % coefficient of the weighted area term A(\phi);        % Note: Choose smaller value of alf (\nu in the paper) if there are weak object boundaies, such as the cell image in demo 1.​% define initial level set function (LSF) as -c, 0, c at points outside, on% the boundary, and inside of a region R, respectively.[nrow, ncol]=size(Img);  c=4;initialLSF=c*ones(nrow,ncol);w=10;initialLSF(w+1:end-w, w+1:end-w)=0;  % zero level set is on the boundary of R.                                      % Note: this can be commented out. The intial LSF does NOT necessarily need a zero level set.                                     initialLSF(w+2:end-w-1, w+2: end-w-1)=-c; % negative constant -c inside of R, postive constant c outside of R.u=initialLSF;figure;imagesc(Img, [0, 255]);colormap(gray);hold on;[c,h] = contour(u,[0 0],'r');                          title('Initial contour');​​% start level set evolutionfor n=1:500    u=EVOLUTION(u, g ,lambda, mu, alf, epsilon, timestep, 1);      pause(0.001);    if mod(n,20)==0        imagesc(Img, [0, 255]);colormap(gray);hold on;        [c,h] = contour(u,[0 0],'r');         iterNum=[num2str(n), ' iterations'];                title(iterNum);        hold off;    endendimagesc(Img, [0, 255]);colormap(gray);hold on;[c,h] = contour(u,[0 0],'r'); totalIterNum=[num2str(n), ' iterations'];  title(['Final contour, ', totalIterNum]);​

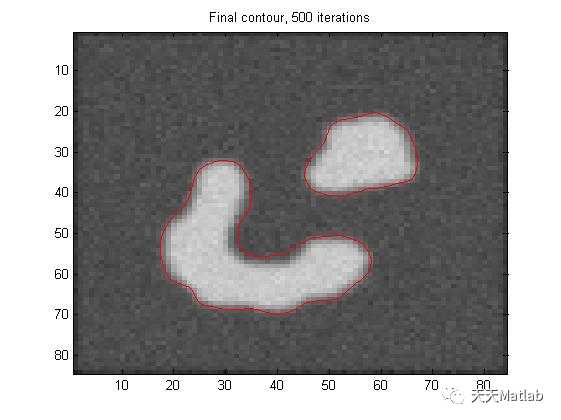
3 仿真结果

4 参考文献

[1]石云峰. 基于Snake模型的图像分割方法研究及应用[D]. 西安电子科技大学, 2009.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。

今天的文章【图像分割】基于snake模型实现图像分割含Matlab源码分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。