用于实时实例分割的Deep Snake算法

  第一部分：创新及其优点

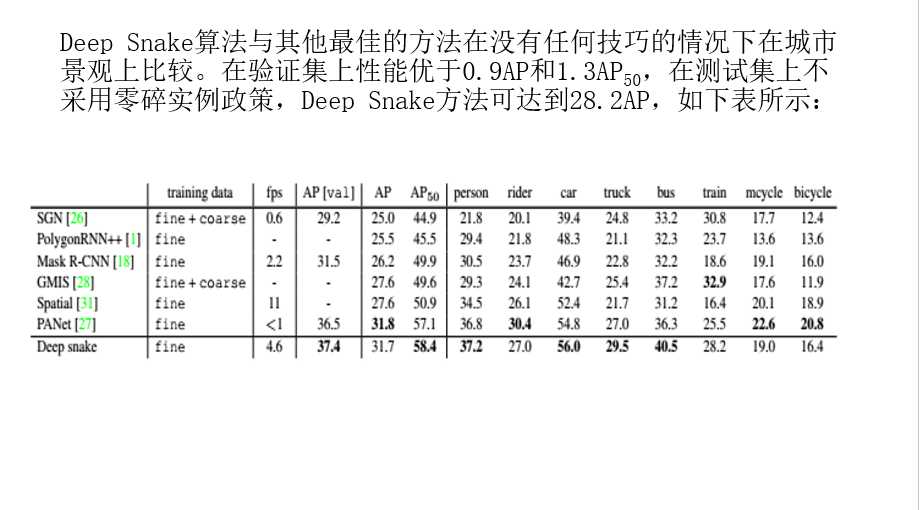
  第二部分：算法原理

  第三部分：实验过程

  第四部分：程序逻辑

1 创新及其优点

Deep Snake算法建立在传统Snake算法的基础上，将snake算法做成了轮廓结构化特征学习的方法，使用了循环卷积取得了比通用的图卷积能更好的挖掘轮廓的周期图结构。

  Deep Snake算法克服了建立在图像检测器给出便捷方框不准确造成实例分割产生误差的缺陷；优化了将图像边框表示成密集二进制带来复杂的后期处理的缺点；同时相比在RGB图中进行轮廓回归更充分的利用了轮廓的特殊拓扑。

2 算法原理

snake是一种主动轮廓模型，它需要一个初始轮廓，以其为输入进行逐步迭代，从而达到调整图像轮廓使其更精确的目的。

snake在逐步迭代优化过程中的目标是能量函数最小化，这个能量函数值轮廓能量和图像能量的总和，其能量函数如下：

     指当前轮廓本身能量(内部能量)， 指图像轮廓对应点的能量(外部能量), 表示其方差的相关项。其中内部能量由两部分组成：一阶导数的模（称为弹性能量）和二阶导数的模（弯曲能量）

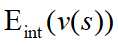
其中内部能量由两部分组成：一阶导数的模（称为弹性能量）和二阶导数的模（弯曲能量）[这里需要记住为什么]，在迭代过程中，弹性能量能快速的把轮廓压缩成光滑的圆；弯曲能量将轮廓拉成光滑的曲线或直线，他们的作用是保持轮廓的光滑和连续性。通常alpha越大，轮廓收敛越快；beta越大，轮廓越光滑。

外部图像能量分三种：线性能量(通常更亮度相关)；边缘能量(图像的边缘组成)；终端能量。在迭代优化过程中，外部能量会使轮廓朝（灰度）高梯度位置靠近。而通常梯度高的位置都是图像中前景与背景的界限或者物体与物体之间、物体内部不同部分的界限，适合用于分割。在逐步迭代优化过程中的目标是能量函数最小化，这就是snake算法调整实例轮廓的方法和过程。

Deep Snake与snake算法类似,分割实例分为两步:初始化轮廓和轮廓变形，然后进行迭代使得实列分割边界更加准确。
      （1） 初始化轮廓：检测包围框初始边缘上的四个中性点的菱形轮廓，然后以菱形为输入,输出四个顶点到对象极值的偏量，构造出八边形作为初始轮廓。
      （2） 轮廓变形：先沿初始化八角形轮廓均匀的采样N个点，通过学习特征和顶点坐标的级联[F(xi):xi](F是特征映射)构造顶点xi得输入特征。在给定轮廓上定义的输入特征后移入特征学习的循环卷积，得到轮廓的输出特征并预测轮廓点与目标点之间的偏移，最后进行不断迭代得到实例的更优轮廓。从而解决了传统snake算法中只能达到局部最优的缺点

不同于snake算法的是，snake算法将顶点的坐标作为一组变量并将变量用于优化能量函数中使其中最小进而达到调整轮廓的目的，而deep snake直接学会以端到端的方式进行轮廓变形.

循环卷积不同于线性卷积的一种卷积运算，是周期卷积的一种。其公式如下：

循环卷积

RN(n)代表只取长度为n的主值序列，其计算过程如下：

蓝色为输入特征、黄色为核函数，令右图所示状态为

n=0，将输入特征变量与核函数变量做乘积得到输出

变量y(0),当n=1时，将核函数逆时针旋转一个单位得

到y(1),不断旋转直到算出y(n)，这样就算出了输入轮

廓的输出特征，最后根据输出特征对初试轮廓进行

调整，从而完成deep snake算法第二步。

值得一提的是由于实例轮廓多是封闭的回路，因此这里运用循环卷积比一般卷积更能运用这种特殊的拓扑结构。

3 实验过程

4 程序逻辑

以上就是本人对deep Snake相关知识点的创新、原理、实验过程、程序逻辑的个人看法，欢迎指正。