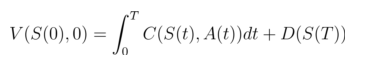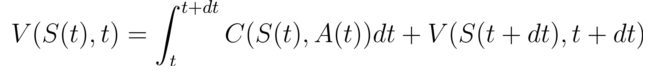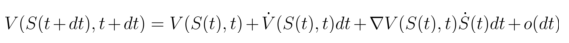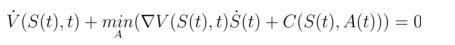参考资料：维基的哈密顿-雅克比-贝尔曼方程条目。有条件的同学可以自行查看，效果比本文要好一些。文末也会给出相关更深入的资料供大家学习。
作为强化学习的一个基础思想，HJB方程从大框架概述了控制优化的方向。这里对其推导与应用进行简述。
定义如下变量：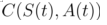
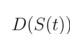
为过程价值函数，其中S(t)为在t时刻的状态函数，A(t)为在t时刻的动作函数。
为在t时刻状态为S(t)的终点值函数。
我们可以定义如下过程：在[0,T]时间段，最终值函数的表现形式如下：
而我们的优化目标就是保证右端公式的最小化。
HJB偏微分形式推导：
考虑如下表达形式：
对右端的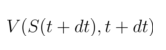
进行泰勒展开，可得到以下形式：
与上式联立可消去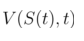
，然后去除dt，可得如下优化形式：
JCB方程微分形式推导得证。
如何求解：
一般采用逆向归纳法，即从t=T推导至t=0，利用动态规划的思想求解。
HJB方程相关资料：
链接：https://pan.baidu.com/s/1pBom-F4cLqHVA3_u3XSOyA?pwd=4s5e
提取码：4s5e
今天的文章HJB方程简述_动态规划与hjb方程分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/47594.html
