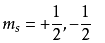四个量子数_描述电子状态的四个量子数

像电子这样的微观粒子，要描述其运动状态，需要使用波函数，而这个波函数是通过求解薛定谔方程得到的。

每个波函数都会涉及到一些量子数，如果只考虑电子的轨道运动，引入3个量子数就够用了

即：n (主量子数), l（角量子数）,m（磁量子数）

如果要考虑电子的自旋运动，还要使用电子的自旋波函数，还要额外引入电子的自旋量子数m_s

主量子数 n

n=1,2,3,4,5,6……正整数

对应K,L,M,N,O,P….电子层

n是决定轨道（或电子）能量的主要量子数

n越大，电子离核平均距离越远，能量越高。

角量子数 l (也称副量子数) 决定电子角动量的大小

l=0,1,2,3,4,5……(n-1)

对应着s,p,d,f,g….电子亚层

l受n限制

n=1时，l=0; 1s亚层

n=2时，l=0,1; 对应2s,2p亚层

n=3时，l=0,1,2; 对应3s,3p,3d亚层

n=4时，l=0,1,2,3; 对应4s,4p,4d,4f亚层.

磁量子数m（决定角动量在Z轴投影的大小）

m=0,±1,±2,±3…….±l;

m决定原子轨道在核外的空间取向

l=0，m=0; s型轨道，只一个取向

l=1,m=0,±1；代表p_z,p_x,p_y3个轨道

l=2,m=0,±1,±2;代表d亚层有d_z²,d_xz,d_yz,d_xy,d_x²-y²   5个取向的轨道

 自旋 量子数 

Ψ_{n,l,m————原子的单电子波函数，又称原子轨道波函数}

例： n=1,l=0,m=0

Ψ_1,0,0=Ψ_1s, 即1s轨道； 

Ψ_2,0,0=Ψ_2s， 即2s轨道；

Ψ_2,1,0=Ψ_2pz， 即2p_z轨道；  

Ψ_3,2,0=Ψ_3dz²， 即3d_z2轨道。

今天的文章四个量子数_描述电子状态的四个量子数分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。