sin函数振幅_怎么判断函数振荡

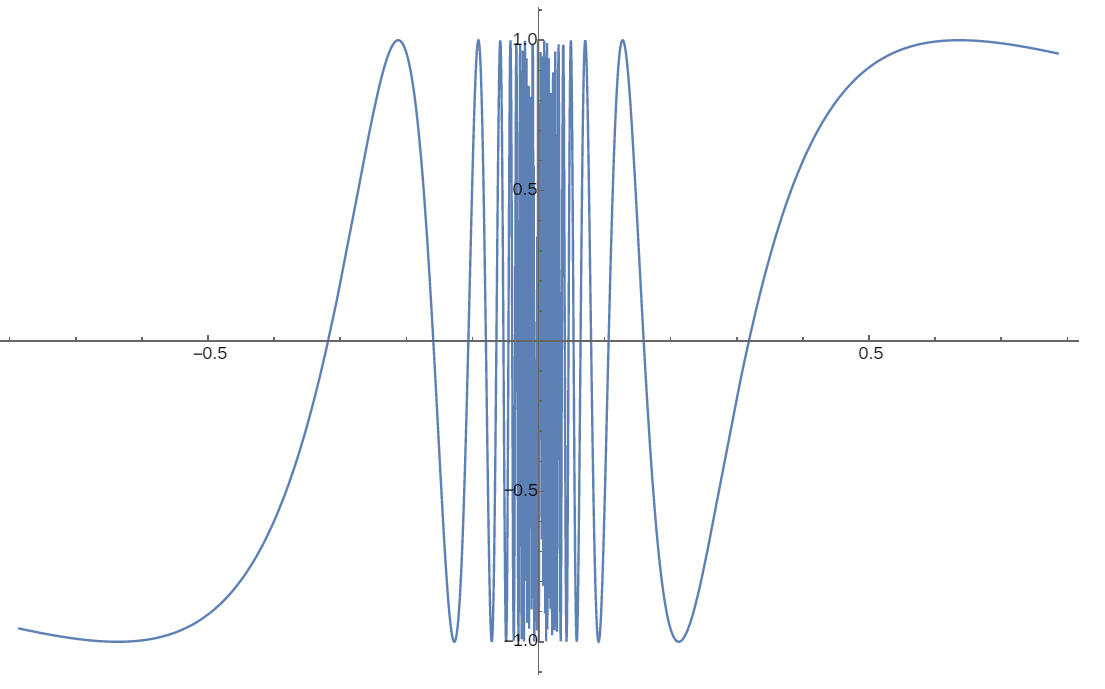
对于\(\sin\frac{1}{x}\)，当\(x\)从0的右侧附近逐渐靠近0时，\(\frac{1}{x}\)的变化是非常大的，比如当\(x\)由\(\frac{1}{10}\)变小到\(\frac{1}{100}\)，仅仅是\(\frac{9}{100} = \mathrm{\Delta}x = \frac{1}{10}\)–\(\ \frac{1}{100}\)的变化就会使得\(\frac{1}{x}\)由10变到100，而由\(\sin 10 = \sin\frac{1}{\frac{1}{10}}\)变到\(\sin 100 = \sin\frac{1}{\frac{1}{100}}\)实际上已经跨过了好几个\(sinx\)的周期（周期是\(2\pi \approx 6.18\)），因此\(\sin\frac{1}{x}\)在\(\frac{1}{10}\)和\(\frac{1}{100}\)之间多次往返于-1和1之间。总之，在0的附近微小的\(x\)变化会引起极大的\(\frac{1}{x}\)的变化，以至于会引起\(\sin\frac{1}{x}\)的变化跨越更多的\(sinx\)的周期，也就是说这种0附近微小的\(x\)变化会使得\(\sin\frac{1}{x}\)在-1和1之间往返很多次，当\(x\)变得越来越小时，\(\frac{1}{x}\)的变化幅度会越来越大，以至于\(\sin\frac{1}{x}\)的图像会更频繁地在-1和1之间往返或震荡，这就是其图像在0附近变得密密麻麻的原因。

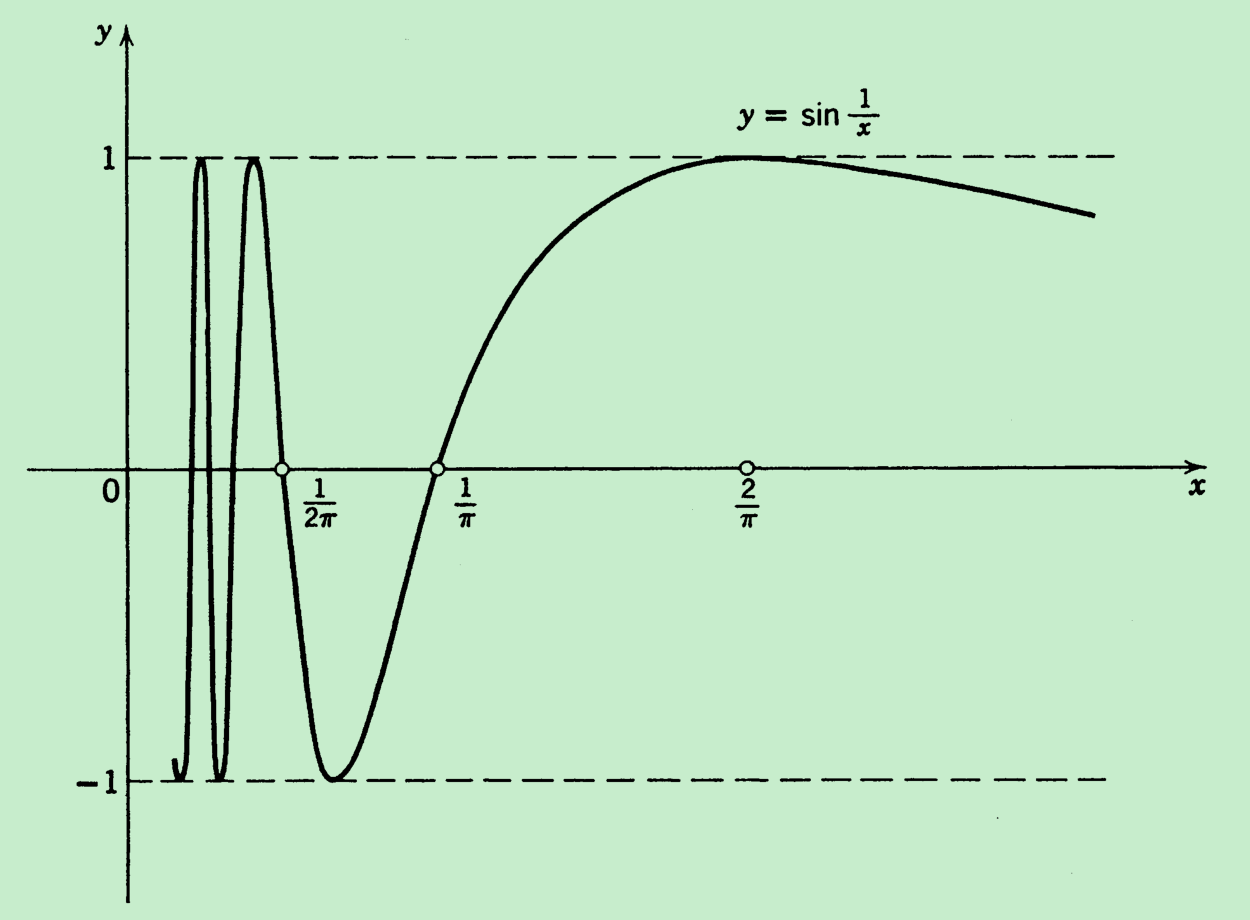
当\(x\)为正且越来越大的时候，\(\frac{1}{x}\)越来越小，当\(\frac{1}{x}\)小于\(\pi\)时（此时由于\(x\)为正所以\(\frac{1}{x} > 0\)），这时候\(\sin\frac{1}{x}\)的值域就是\(sinx\)于\((0,\pi)\)上的情况——函数图像为正，换句话说当\(x\)大于\(\frac{1}{\pi}\)时\(\sin\frac{1}{x}\)的图像就一直为正，如下图所示。

¹

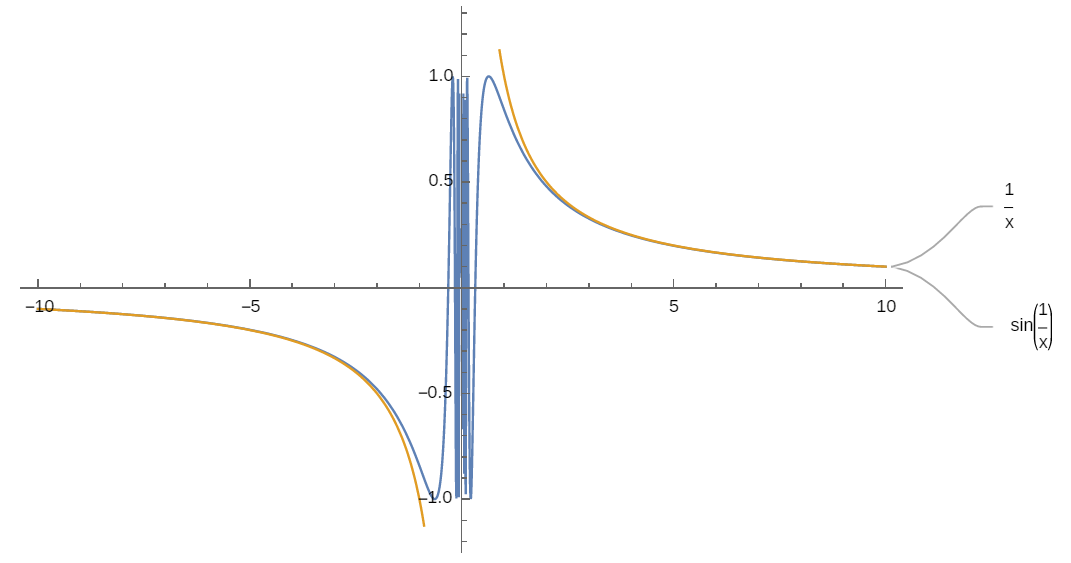
另一方面，根据\(\lim_{x \rightarrow 0}\frac{sinx}{x} = 1\)有\(\lim_{x \rightarrow \infty}\frac{\sin\frac{1}{x}}{\frac{1}{x}} = 1\)，也就是说当\(x\)非常大的时候\(\sin\frac{1}{x}\)和\(\frac{1}{x}\)的值便会非常接近，这就是为什么\(\sin\frac{1}{x}\)和\(\frac{1}{x}\)的图像在\(x\)越来越大时会越来越靠近的原因。

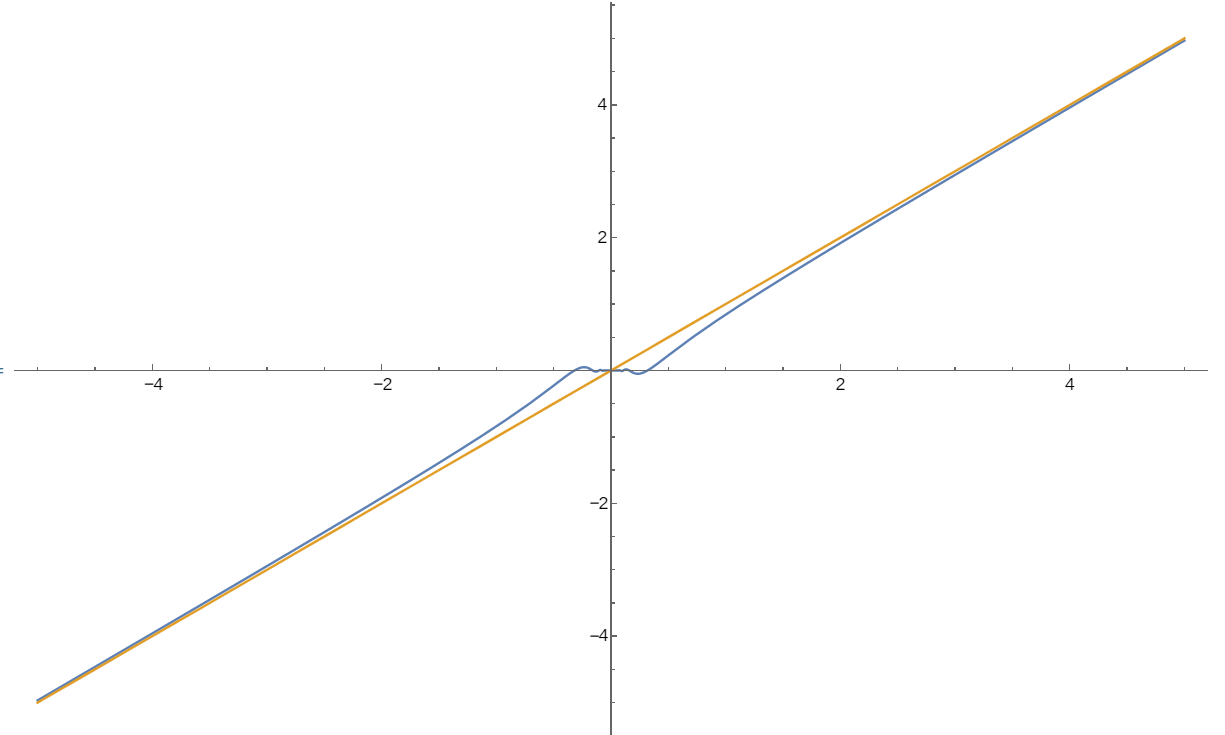
同样地我们还可以解释为什么\(x\)非常大时\({x^{2}\sin}\frac{1}{x}\)和\(x\)的图像非常接近（这种情况下\({x^{2}\sin}\frac{1}{x} \approx {x^{2} \times}\frac{1}{x} = x\)）。

对于\(x\)为负的情况，我们可以简单地根据\(\sin\frac{1}{x}\)为奇函数这个性质得出相应的情况。

今天的文章sin函数振幅_怎么判断函数振荡分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。