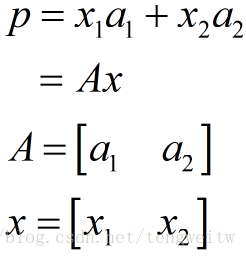正交投影矩阵是什么_线性代数向量内积公式

注意这里我们的投影是向量的投影，几何的投影(并不一定是垂直投影的)可见度娘百科。

相同的，我们从简单的二维投影来開始讨论。

   1、二维投影

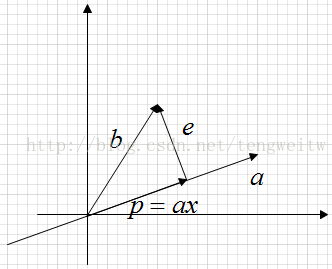
上图表示的是，向量b在向量a上的投影。显然有例如以下表达式：

<img src=”https://img-blog.csdn.net/20141116175319046?

watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvdGVuZ3dlaXR3/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast” width=”482″ height=”214″ alt=””>

当中，P为投影矩阵，由P的表达式能够看出，它具有例如以下性质：

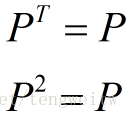
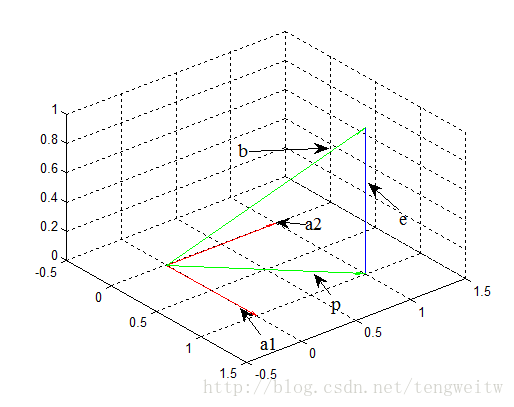
2、三维投影

因为e垂直平面，则e向量垂直与平面中的随意向量。则有：

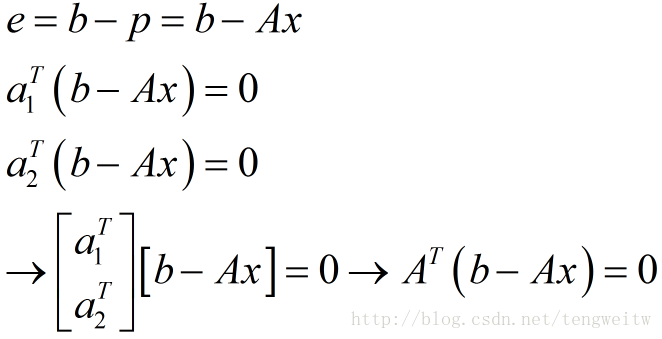
将上式化简求得x：

<img src=”https://img-blog.csdn.net/20141116175619071?

watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvdGVuZ3dlaXR3/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast” width=”128″ height=”76″ alt=””>

又由于p=Ax，Pb=p，则得到投影矩阵为：

由P的表达式能够看出，它具有例如以下性质：

<img src=”https://img-blog.csdn.net/20141116175706183?

watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvdGVuZ3dlaXR3/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast” width=”69″ height=”59″ alt=””>

上面的投影矩阵是通式。当投影在一维情况时，A即为直线上的随意一个向量a,投影矩阵为：

<img src=”https://img-blog.csdn.net/20141116175728444?

watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvdGVuZ3dlaXR3/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast” width=”361″ height=”55″ alt=””>

3、举例说明

如上图，如果我们要将向量b投影到水平面上。其投影为p，a1,a2为水平面的两个线性无关向量，它们的參数分别为：

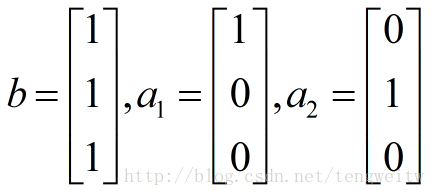
那么A=[a1 a2]即：

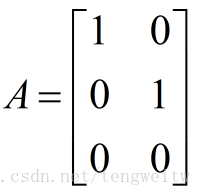
由上面我们求得的通式，可得投影矩阵P:

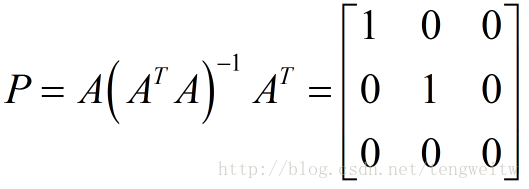
知道投影矩阵P后。我们能够得到b在水平面上的投影p为：

<img src=”https://img-blog.csdn.net/20141116175926614?

watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvdGVuZ3dlaXR3/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast” width=”308″ height=”124″ alt=””>

三维图的matlab程序例如以下：

clear all
clc
 
a1=[1 0 0];
a2=[0 1 0];
b=[1 1 1];
p=[1 1 0];
e=b-p;
quiver3(0,0,0,a1(1),a1(2),a1(3),1,'color','r')
hold on
quiver3(0,0,0,a2(1),a2(2),a2(3),1,'color','r')
hold on
quiver3(0,0,0,b(1),b(2),b(3),1,'color','g')
hold on
quiver3(0,0,0,p(1),p(2),p(3),1,'color','g')
hold on
quiver3(p(1),p(2),p(3),e(1),e(2),e(3),1,'color','b')

原文：http://blog.csdn.net/tengweitw/article/details/41174555

作者：nineheadedbird