skiplist原理_差异分析

SkipList

　　俗称跳表，跳表是一种随机化的数据结构，目前开源软件 Redis 和 LevelDB 都有用到它，它的效率和红黑树以及 AVL 树不相上下，但跳表的原理相当简单，只要你能熟练操作链表，就能轻松实现一个 SkipList。

有序表的搜索

考虑一个有序表：

从该有序表中搜索元素 < 23, 43, 59 > ，需要比较的次数分别为 < 2, 4, 6 >，总共比较的次数

为 2 + 4 + 6 = 12 次。有没有优化的算法吗?  链表是有序的，但不能使用二分查找。类似二叉

搜索树，我们把一些节点提取出来，作为索引。得到如下结构：

这里我们把 < 14, 34, 50, 72 > 提取出来作为一级索引，这样搜索的时候就可以减少比较次数了。

我们还可以再从一级索引提取一些元素出来，作为二级索引，变成如下结构：

这里元素不多，体现不出优势，如果元素足够多，这种索引结构就能体现出优势来了。

这基本上就是跳表的核心思想，其实也是一种通过“空间来换取时间”的一个算法，通过在每个节点中增加了向前的指针，从而提升查找的效率。

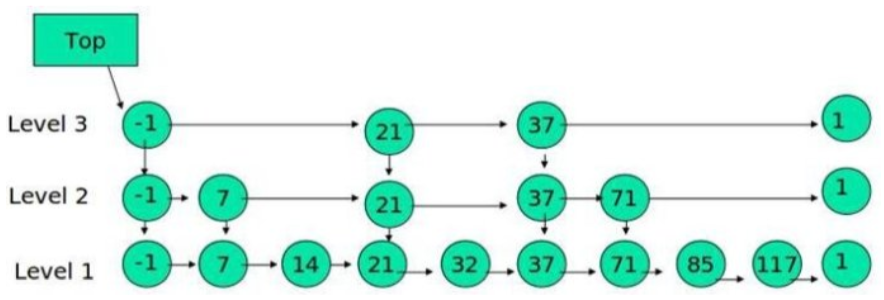
跳表

下面的结构是就是跳表：

其中 -1 表示 INT_MIN， 链表的最小值，1 表示 INT_MAX，链表的最大值。

跳表具有如下性质：

(1) 由很多层结构组成

(2) 每一层都是一个有序的链表

(3) 最底层(Level 1)的链表包含所有元素

(4) 如果一个元素出现在 Level i 的链表中，则它在 Level i 之下的链表也都会出现。

(5) 每个节点包含两个指针，一个指向同一链表中的下一个元素，一个指向下面一层的元素。

跳表的搜索

例子：查找元素 117

(1) 比较 21， 比 21 大，往后面找

(2) 比较 37,   比 37大，比链表最大值小，从 37 的下面一层开始找

(3) 比较 71,  比 71 大，比链表最大值小，从 71 的下面一层开始找

(4) 比较 85， 比 85 大，从后面找

(5) 比较 117， 等于 117， 找到了节点。

具体的搜索算法如下：

C代码

1.

3. find(x)  

4. { 

5.     p = top; 

6. while (1) { 

7. while (p->next->key < x) 

8.             p = p->next; 

9. if (p->down == NULL)  

10. return p->next; 

11.         p = p->down; 

12.     } 

13. } 

跳表的插入

先确定该元素要占据的层数 K（采用丢硬币的方式，这完全是随机的）

然后在 Level 1 … Level K 各个层的链表都插入元素。

例子：插入 119， K = 2

如果 K 大于链表的层数，则要添加新的层。

例子：插入 119， K = 4

丢硬币决定 K

插入元素的时候，元素所占有的层数完全是随机的，通过一下随机算法产生：

C代码

1. int random_level() 

2. { 

3.     K = 1; 

4.

5. while (random(0,1)) 

6.         K++; 

7.

8. return K; 

9. } 

相当与做一次丢硬币的实验，如果遇到正面，继续丢，遇到反面，则停止，

用实验中丢硬币的次数 K 作为元素占有的层数。显然随机变量 K 满足参数为 p = 1/2 的几何分布，

K 的期望值 E[K] = 1/p = 2. 就是说，各个元素的层数，期望值是 2 层。

跳表的高度。

n 个元素的跳表，每个元素插入的时候都要做一次实验，用来决定元素占据的层数 K，

跳表的高度等于这 n 次实验中产生的最大 K，待续。。。

跳表的空间复杂度分析

根据上面的分析，每个元素的期望高度为 2， 一个大小为 n 的跳表，其节点数目的

期望值是 2n。

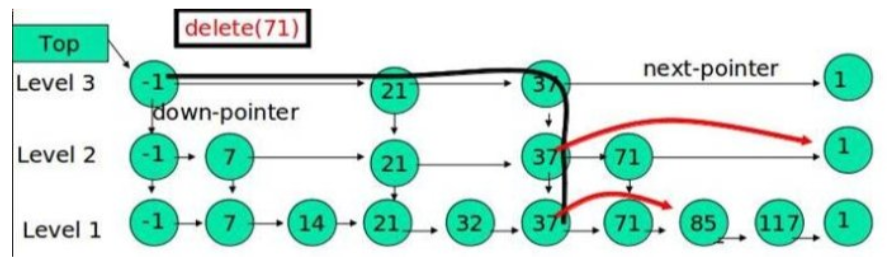
跳表的删除

在各个层中找到包含 x 的节点，使用标准的 delete from list 方法删除该节点。

例子：删除 71

源地址：http://kenby.iteye.com/blog/1187303

今天的文章skiplist原理_差异分析分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。