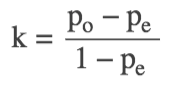kappa计算结果为-1~1，通常kappa是落在 0~1 间，可分为五组来表示不同级别的一致性：
| 0.0~0.20 | 极低的一致性(slight) |
| 0.21~0.40 | 一般的一致性(fair) |
| 0.41~0.60 | 中等的一致性(moderate) |
| 0.61~0.80 | 高度的一致性(substantial) |
| 0.81~1 | 几乎完全一致(almost perfect) |
计算公式：
po是每一类正确分类的样本数量之和除以总样本数.
假设每一类的真实样本个数分别为a1,a2,...,aC，预测出来的每一类的样本个数分别为b1,b2,...,bC，总样本个数为n，则有：pe=（a1×b1+a2×b2+...+aC×bC） / （n×n）.
举例分析：
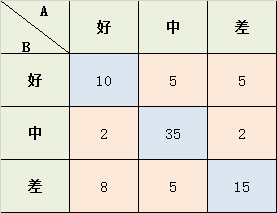
学生考试的作文成绩，由两个老师给出 好、中、差三档的打分，现在已知两位老师的打分结果，需要计算两位老师打分之间的相关性kappa系数：
Po = (10+35+15) / 87 = 0.689
a1 = 10+2+8 = 20; a2 = 5+35+5 = 45; a3 = 5+2+15 = 22;
b1 = 10+5+5 = 20; b2 = 2+35+2 = 39; b3 = 8+5+15 = 28;
Pe = (a1*b1 + a2*b2 + a3*b3) / (87*87) = 0.455
K = (Po-Pe) / (1-Pe) = 0.4293578
from sklearn.svm import SVC from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.metrics import confusion_matrix X,y = make_classification() X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3) svc = SVC() svc.fit(X_train,y_train) y_pred = svc.predict(X_test) result = confusion_matrix(y_test, y_pred) def kappa_coefficient(confusion_matrix): """ descibe:compute kappa coefficient param confusion_matrix:matrix return kappa coefficient """ import numpy as np P_0 = 0 for i in range(len(confusion_matrix)): P_0 = P_0+confusion_matrix[i,i] a = [] b = [] for i in range(len(confusion_matrix)): a.append(sum(confusion_matrix[i])) b.append(sum(confusion_matrix[:,i])) P_e = sum(np.array(a)*np.array(b))/(sum(a)*sum(a)) kappa = (P_0/sum(a)-P_e)/(1-P_e) return kappa kappa_coefficient(confusion_matrix=result)
今天的文章kappa系数分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/55273.html
