代价函数

代价函数：又称损失函数，我的理解是用于更好地拟合样本，得到更合适模型的一个方法。

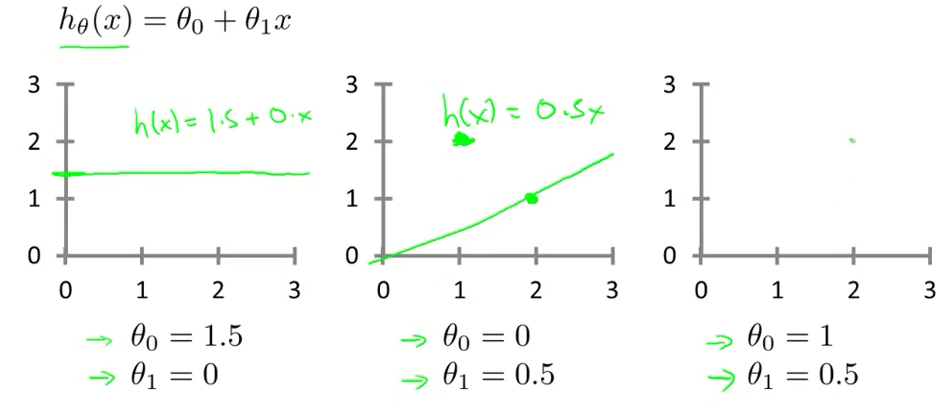
在线性回归中，假设函数为 h_θ(x) = θ_{0 +} θ_{1 *} x ，其中θ₀和θ₁的变化会引起假设函数的变化，参数的选择决定了我们得到的直线相对于训练集的准确度。

为了让预测值和真实值的误差尽可能小和最小化θ₀和θ₁，我们将这个问题转化为找到能使训练集中预测值和真实值的差的平方的和的1/2M最小的θ₀和 θ₁的值。

于是我们定义

为代价函数，又称为平方误差函数，它是解决回归问题最常用的手段。其中 m 代表训练集样本数量, xⁱ  代表第 i 个样本，h_θ(xⁱ) 代表第 i 个样本对应的预测值， yⁱ 代表第 i 个样本对应的真实值。

更直观地理解代价函数

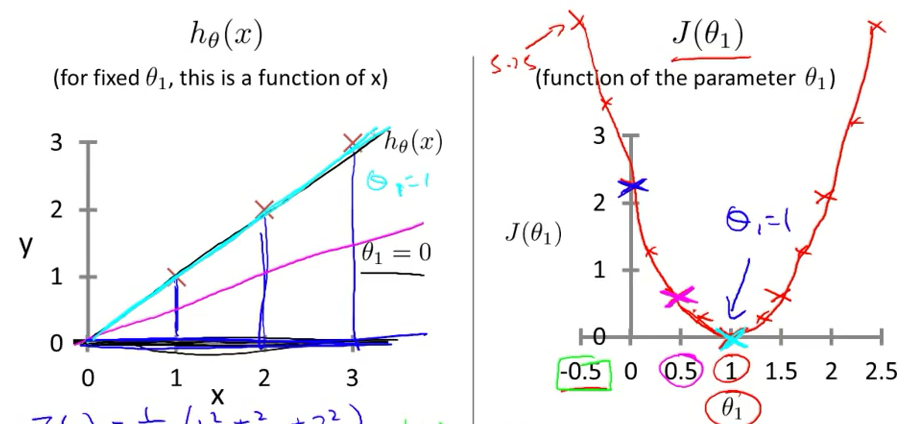
为了更加直观的理解代价函数，首先我们先令θ₀ = 0，并选取不同的θ₁作为假设函数的参数θ₁，通过不同的模型和代价函数，可得出代价函数 J(θ₁) 与 θ₁的关系如下图:

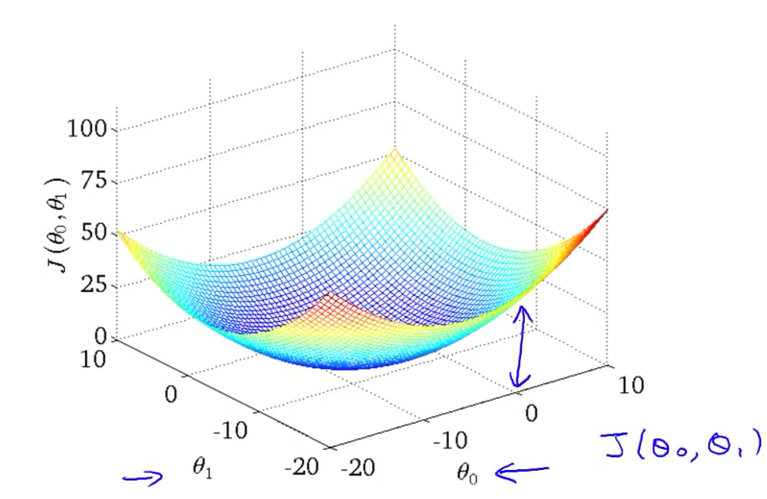
这次我们分别选取不同的θ₀和θ₁，引入不同的模型，作出J(θ₁) 与 θ_1、的θ₀ 关系图如下：

这是一个碗状的3D图， 碗底即代价函数 J(θ_0，θ₁)  的最低点，对应的θ₀和θ₁即为最小。

今天的文章代价函数分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。