Simulink之低通滤波
低通滤波,从字面意思理解就是低频信号可以通过,高频信号会被滤掉,主要用于去除信号的毛刺和干扰,工程上应用较多。
低通滤波器的基本理论公式是:
y(t) = K*u(t) + (1-K)*y(t-1) = y(t-1) + K*[u(t)-y(t-1)]
其中,K=dT/T,K一般介于0~1之间,dT是运行步长,T是时间常数;u是输入信号;y是输出信号。
一般对于某一个控制器,其运行周期是一定的,所以只能调整时间常数来改变滤波效果。
基于以上公式我们先搭建一个基本的低通滤波器simulink模型,如下图:
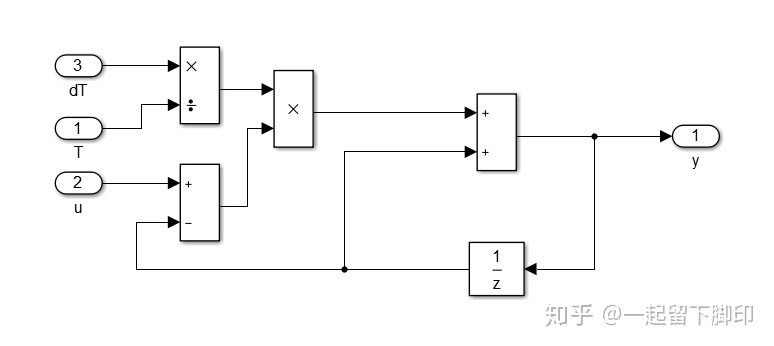
从图中可以看出,滤波器的输出就是上一时刻输出,再加上一个比例因子乘以当前输入减去上一时刻输出。可以试想,如果该比例因子为1(即T=dT),当前时刻输出就等于输入;如果该比例因子处于0~1之间,当前时刻输出肯定要慢于输入,就会产生迟滞,带来的好处就是输入有突然的较大变化时也会被这个比例因子衰减。所以,低通滤波器的优势就是可以滤掉较大高频波动,缺点是相比于原始信号会有延迟。
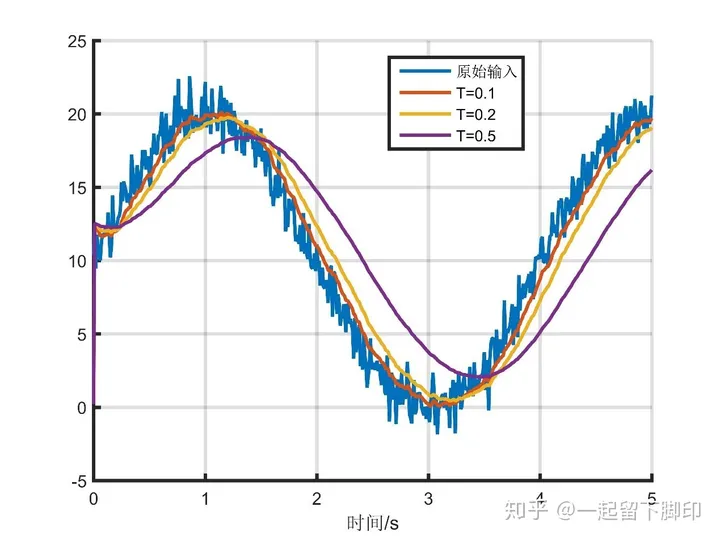
我们给上面的低通滤波器模型加上输入和设定好不同的时间常数(0.1、0.2、0.5),对比输入信号和滤波之后的信号如下:
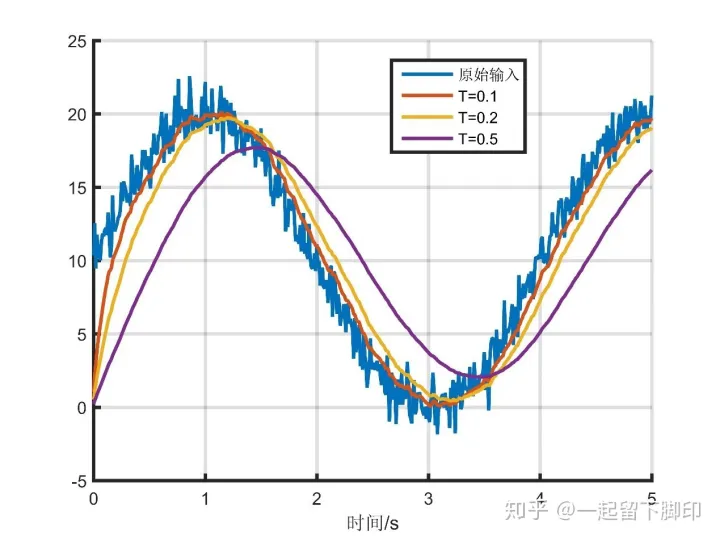
可以看出,滤波之后信号变平滑了,同时随着时间常数T的增大,滤波后的曲线延迟也越大。所以在实际使用时,时间常数T的选择特别重要,需要我们综合考虑控制系统对信号精度和信号延迟的要求,选择符合我们要求的时间常数。
Simulink中也有自带的模拟量滤波器,如下图所示。
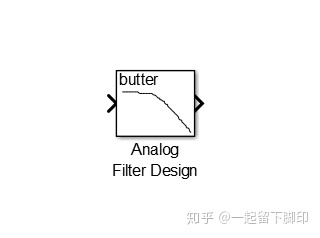
将该滤波器类型设置为Lowpass,截止频率设置为5,如下图所示。
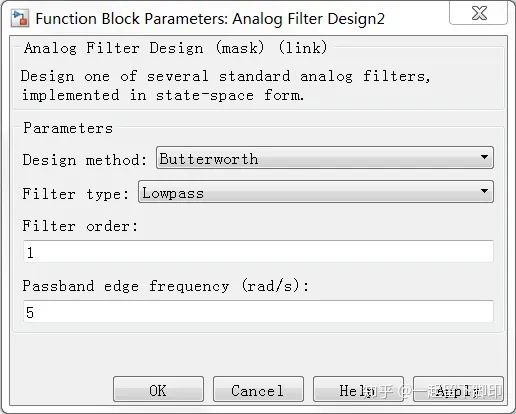
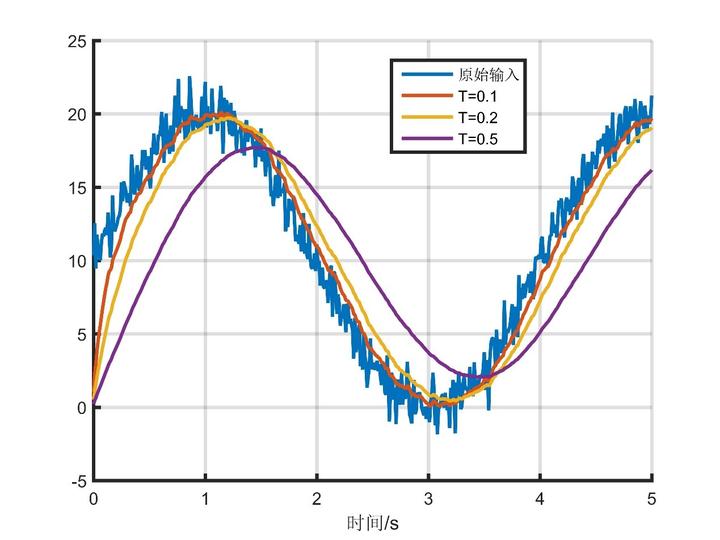
采用相同的原始信号进行仿真,与前面时间常数为0.2s的数据进行对比如下图,发现我们搭建的滤波时间常数为T=0.2s与simulink自带的截止频率为5滤波器滤波效果完全一致。如果感兴趣的话,这两个设置参数的内部关系大家可以自行研究。
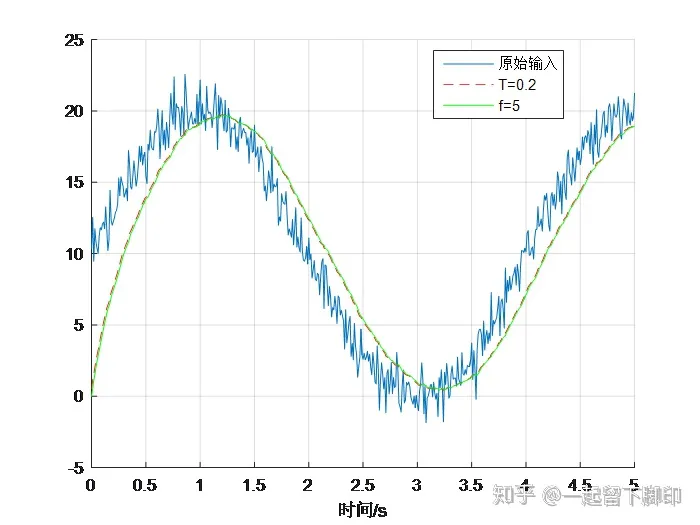
到这里好像差不多可以结束了。不过再仔细看看滤波后的数据,是不是还有其他问题:原始数据是从10开始的,滤波结果是从0开始的,这会导致系统刚开始运行时,输入信号偏差太大,产生失真,这是不允许的。
问题出在哪里呢?再看看滤波器的simulink模型,1/Z的初始值为0,所以滤波器只能从0开始计算。所以我们考虑需要在系统刚开始运行时,需要把输入的初始值作为滤波器的计算起始点,模型我们改成这样:
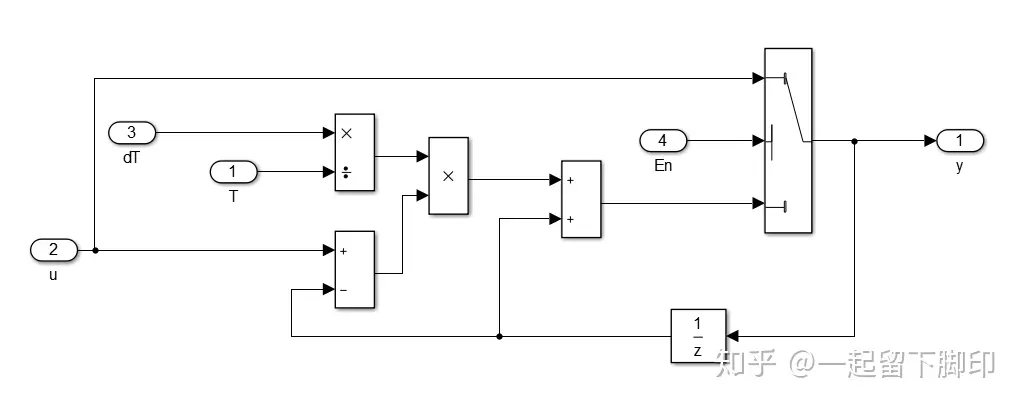
到系统刚运行时,会置位1次使能信号(图中的输入4),这样就可以把滤波器计算的起点与输入信号同步了,仿真结果如下: