算法09 五大查找之：哈希查找

前面的几篇文章分别总结了：顺序查找、二分查找、索引查找、二叉排序树。这一篇文章要总结的是五大查找的最后一个：哈希查找（也称为散列查找）。提起哈希，我的第一印象就是java中的Hashtable类，它是由 key/value 的键值对组成的集合，它就是应用了哈希技术。

那什么是哈希查找呢？在弄清楚什么是哈希查找之前，我们要弄清楚哈希技术，哈希技术是在记录的存储位置和记录的 key 之间建立一个确定的映射 f()，使得每个 key 对应一个存储位置 f(key)。若查找集合中存在这个记录，则必定在 f(key) 的位置上。哈希技术既是一种存储方法，也是一种查找方法。

六种哈希函数 f(key) 的构造方法：

1、直接定址法

哈希地址：f(key) = a*key+b (a,b为常数)

这种方法的优点是：简单，均匀，不会产生冲突。但是需要事先知道 key 的分布情况，适合查找表较小并且连续的情况。

2、数字分析法

比如我们的11位手机号码“136xxxx5889”，其中前三位是接入号，一般对应不同运营公司的子品牌，如130是联通如意通，136是移动神州行等等。中间四位表示归属地。最后四位才是用户号。

若我们现在要存储某家公司员工登记表，如果用手机号码作为 key，那么极有可能前7位都是相同的，所以我们选择最后四位作为 f(key) 就是不错的选择。

3、平方取中法

故名思义，比如 key 是1234，那么它的平方就是1522756，再抽取中间的3位就是227作为 f(key) 。

4、折叠法

折叠法是将 key 从左到右分割成位数相等的几个部分(最后一部分位数不够可以短些)，然后将这几部分叠加求和，并按哈希表的表长，取后几位作为 f(key) 。

比如我们的 key 是 9876543210，哈希表的表长为3位，我们将 key 分为4组，987|654|321|0 ，然后将它们叠加求和 987+654+321+0=1962，再取后3位即得到 f(key) = 962 。

5、除留余数法

哈希地址：f(key) = key mod p (p<=m) m为哈希表表长。

这种方法是最常用的哈希函数构造方法。下面的代码中也使用了这种方法。

6、随机数法

哈希地址：f(key) = random(key)

这里 random 是随机函数，当 key 的长度不等时，采用这种方法比较合适。

哈希函数冲突的两种解决方法：

我们设计得再好的哈希函数也不可能完全避免冲突，当我们使用哈希函数后发现有 key1 != key2，但却有 f(key1) = f(key2) ，即发生冲突。

1、开放定址法：

开放定址法就是一旦发生了冲突，就去寻找下一个空的哈希地址，只要哈希表足够大，空的哈希地址总是能找到，然后将记录插入。这种方法是最常用的解决冲突的方法。下面的代码中也使用了这种方法。

2、链地址法：

链地址法不做详细展开。

代码：

HashSearch.java

import java.io.IOException;
import java.util.Scanner;

public class HashSearch {
    // 初始化哈希表
    static int hashLength = 7;
    static int[] hashTable = new int[hashLength];

    // 原始数据
    static int[] list = new int[]{13, 29, 27, 28, 26, 30, 38};

    public static void main(String[] args) throws IOException {
        System.out.println("*******哈希查找*******");

        // 创建哈希表
        for (int i = 0; i < list.length; i++) {
            insert(hashTable, list[i]);
        }
        System.out.println("展示哈希表中的数据：" + display(hashTable));

        while (true) {
            // 哈希表查找
            System.out.print("请输入要查找的数据：");
            int data = new Scanner(System.in).nextInt();
            int result = search(hashTable, data);
            if (result == -1) {
                System.out.println("对不起，没有找到！");
            } else {
                System.out.println("数据的位置是：" + result);
            }
        }
    }

    /**
     * 方法：哈希表插入
     */
    public static void insert(int[] hashTable, int data) {
        // 哈希函数，除留余数法
        int hashAddress = hash(hashTable, data);

        // 如果不为0，则说明发生冲突
        while (hashTable[hashAddress] != 0) {
            // 利用 开放定址法 解决冲突
            hashAddress = (++hashAddress) % hashTable.length;
        }

        // 将待插入值存入字典中
        hashTable[hashAddress] = data;
    }

    /**
     * 方法：哈希表查找
     */
    public static int search(int[] hashTable, int data) {
        // 哈希函数，除留余数法
        int hashAddress = hash(hashTable, data);

        while (hashTable[hashAddress] != data) {
            // 利用 开放定址法 解决冲突
            hashAddress = (++hashAddress) % hashTable.length;
            // 查找到开放单元 或者 循环回到原点，表示查找失败
            if (hashTable[hashAddress] == 0 || hashAddress == hash(hashTable, data)) {
                return -1;
            }
        }
        // 查找成功，返回下标
        return hashAddress;
    }

    /**
     * 方法：构建哈希函数（除留余数法）
     *
     * @param hashTable
     * @param data
     * @return
     */
    public static int hash(int[] hashTable, int data) {
        return data % hashTable.length;
    }

    /**
     * 方法：展示哈希表
     */
    public static String display(int[] hashTable) {
        StringBuffer stringBuffer = new StringBuffer();
        for (int i : hashTable) {
            stringBuffer = stringBuffer.append(i + " ");
        }
        return String.valueOf(stringBuffer);
    }
}

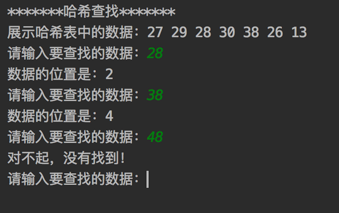
运行结果：

欢迎转载，但请保留文章原始出处

本文地址：http://www.cnblogs.com/nnngu/p/8307743.html

今天的文章算法09 五大查找之：哈希查找分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/57237.html