象棋中马有几种走法_国际象棋马的走法及吃子方法

一、概述

LeetCode双周赛的第二题：输入一个坐标，马从（0,0）开始走，走到该坐标所需要的最短步数。

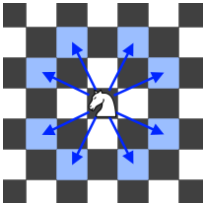
如图马能往八个方向走。我的第一个思路就是DFS，开始没想到循环问题，所以时间溢出，然后使用二维数组记录，可以得到一个结果，但不是最终的结果，我得不到最短的路径。事实证明DFS走不通，应该换别的方法。

另外说一句，这次四道题，第一道和第三道纯粹签到题，第二道也就是这道有一点难，最后一道可能得用DP，然而DP我就没学过，所以就扔了。只做出来两道签到题感觉自己很菜。

二、分析

1、我的方法

就是从0开始，将八个方向编号然后递归。

由于棋盘的对称性，将目标坐标全取绝对值也能得到相同的结果，这样就减少了条件判断。

递归出口我设置为与目标坐标相等或者递归坐标超过目标坐标2格就返回。另外遇到之前走过的各自也返回。

代码如下：

class Solution { int node[300][300] = { 0 }; int result = 0; void DFS(int x, int y, int tx, int ty, int step) { //cout << " x: "<<x << " y: " << y << " "; if (x == tx&&y == ty) { result = step; return; } else if (x > tx + 2 || x < tx-2 ||y>ty+2||y<ty-2) return; else if (node[x+150][y+150] == 1) return; else { node[x+150][y+150] = 1; for (int i = 0; i<8; i++) { //cout << i<<" "; if (result != 0) return; switch (i) { case 0: DFS(x + 2, y + 1, tx, ty, step + 1); break; case 1: DFS(x + 1, y + 2, tx, ty, step + 1); break; case 2: DFS(x - 1, y + 2, tx, ty, step + 1); break; case 3: DFS(x - 2, y + 1, tx, ty, step + 1); break; case 4: DFS(x - 2, y - 1, tx, ty, step + 1); break; case 5: DFS(x - 1, y - 2, tx, ty, step + 1); break; case 6: DFS(x + 1, y - 2, tx, ty, step + 1); break; case 7: DFS(x + 2, y - 1, tx, ty, step + 1); break; } } } } public: int minKnightMoves(int x, int y) { x = abs(x); y = abs(y); int x_=0,y_=0; int step=0; while(x_<x) { x_=x_+2; y_=y_+1; step++; } DFS(x_, y_, x, y,step); return result; } };

这种方法只能找到结果，没法找到最优结果。

2、正确的方法

第一个是uwi的方法，实话实说，我没看懂：

class Solution { public int minKnightMoves(int x, int y) { return (int)knightDistance(x, y); } public long knightDistance(long r, long c) { r = Math.abs(r); c = Math.abs(c); if(r + c == 0)return 0; if(r + c == 1)return 3; if(r == 2 && c == 2)return 4; long step = Math.max((r+1)/2, (c+1)/2); step = Math.max(step, (r+c+2)/3); step += (step^r^c)&1; return step; } }

前面几个判断看懂了，就是从0,0到2,2要四步，到0,1要三步。之后的处理无法理解。于是看另外一个老哥的代码：

int dx[] = {-2, -2, -1, -1, 1, 1, 2, 2}; int dy[] = {-1, 1, -2, 2, -2, 2, -1, 1}; int H[888][888]; class Solution { public: using pii = pair<int, int>; int minKnightMoves(int x, int y) { int xt = abs(x); int yt = abs(y); for (int i = -321; i <= 321; ++ i) for (int j = -321; j <= 321; ++ j) H[i+400][j+400] = -1; H[0+400][0+400] = 0; queue<pii> Q; Q.push({0, 0}); while (!Q.empty()) { auto [x, y] = Q.front(); Q.pop(); if (x == xt && y == yt) return H[x+400][y+400]; for (int k = 0; k < 8; ++ k) { int tx = x+dx[k], ty = y+dy[k]; if (H[tx+400][ty+400] == -1) { H[tx+400][ty+400] = H[x+400][y+400]+1; Q.push({tx, ty}); if (tx == xt && ty == yt) return H[tx+400][ty+400]; } } } return -1; } };

这就友好多了。

首先，我们开一个二维数组作为棋盘，元素赋为-1，即所有未走过的元素都赋值为-1。那么有一个问题，0,0不能在中间，因为数组下标不能有负数。于是我们需要给输入的坐标到二维数组的下标做一个映射：各加350，让700*700的棋盘中350,350作为下标。然后BFS标准写法。对于这种坐标题目，用pair会很方便，这点要学习。

BFS标准写法是什么呢？先开队列，起点进队，开循环，循环退出条件为队列空。拿出队首元素，开始子循环，子循环中入队即可。

有一个地方不要混淆，就是队列中存的坐标不带偏置，到了棋盘上才要加偏置，棋盘中的元素就是走到这里要用的步数。

这个算法要是用图像来表示，类似一朵烟花。第一次循环有8个1，第二次循环8个1周围各出现8个2……这样就保证了最短距离，因为每次本质都是走一步，走一步一定是最短的。

三、总结

BFS好久没写，手生了，没想到这个。不然还是不难的，写出来又能前进好多名。

今天的文章
象棋中马有几种走法_国际象棋马的走法及吃子方法分享到此就结束了，感谢您的阅读。