北大数据结构与算法B课程作业_北大数据结构与算法附录B

目录

 为什么要引入B-树

 BTNode

B-树的上溢-裂点

B-树的下溢

函数总览

search

insert

remove

代码：

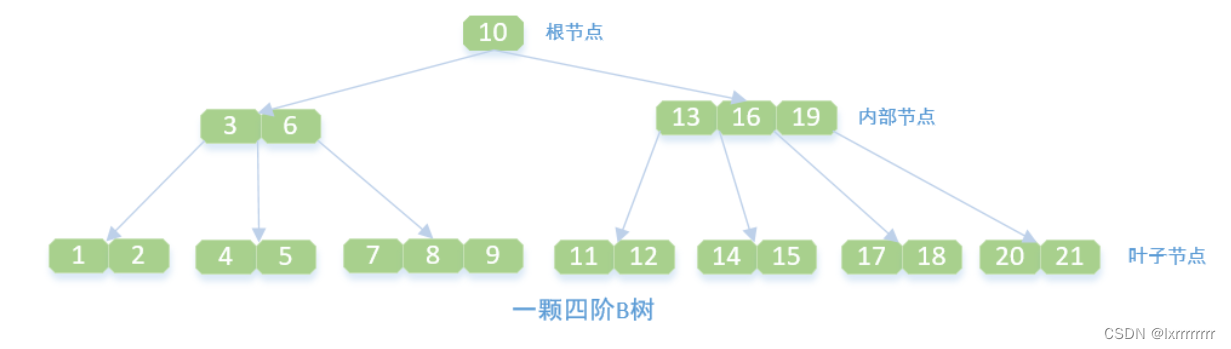
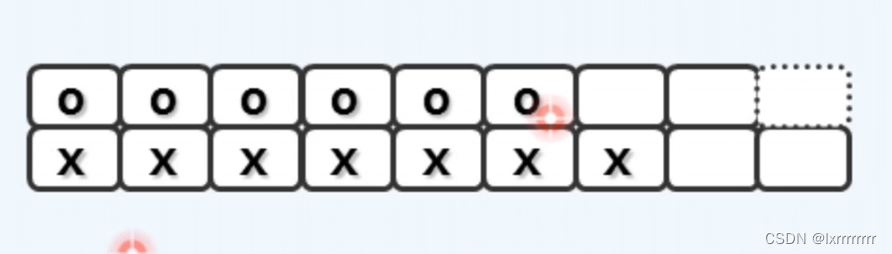
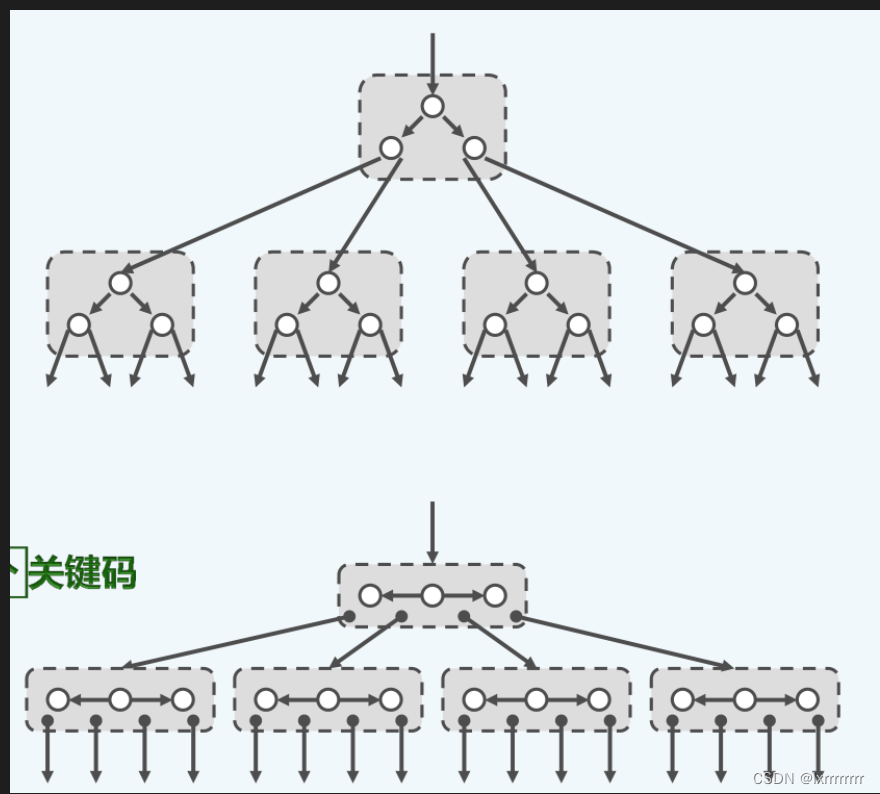
B树其实是由二叉搜索树变化而来，它的本质仍然是二叉搜索树。如下面的图所示，将原有的二叉搜索树的结点进行适当的合并，得到超级结点。由这些超级结点组成的新的树，就是一棵B树。

 为什么要引入B-树

这里就需要考虑多级存储系统了。考虑某个大型数据文件在某低级存储介质上（如硬盘）以二叉平衡树AVL的形式组织。假如该文件的大小为1G，即。这样每次查找至多需要30次I/O操作。我们知道，不同存储介质之间的访问速度差异往往是巨大的，例如内存的访问速度大约是硬盘的倍，尽管最坏情况下也只需要30次访问，但是这样30次硬盘访问操作的代价其实是非常巨大的。

而如果采用B树的话，我们已经注意到，树的整体高度会显著降低。此时的问题是，每次需要从外存中读入一个超级结点，它可能包含了许许多多先前的普通结点，对这样超级结点的I/O操作需要花费的时间又如何呢？

得益于外存访问的缓存机制，从外存中访问一个数据或者是多个数据，它们需要的时间几乎是没有区别的。这是因为在硬件的设计中，不同层次存储器之间往往设置一个buffer，用来缓冲读写的数据，基于此，外存可以提供对批量访问的高效支持。这样，从外存中读取一个超级结点和读取一个普通结点，其时间代价几乎是一样的，而由于B树高度相较于传统的BST显著降低，在多级存储系统中，采用B树可以大大减少I/O次数。

所谓m阶B树，本质是m路平衡搜索树。树中的每个结点，除根结点外，至多拥有m个分支，但是至少也要拥有个分支，对于根结点，可以只拥有两个分支，但不可以少于两个分支。

例如经典的一颗2-4树，也称四阶B树，形状如下图

 BTNode

通过以上的定义，我们知道B-tree的每个节点是一个集合而非一个点

所以我们要重写节点类

每一个节点有两个序列，第一个序列代表他自己的value，第二个序列代表他子节点的引用

这里B树作为BST的衍生，其节点仍然是局部有序的

对于每一个超级节点中的子节点，其左子树必不大于此节点，其右子树必不小于此节点

也就是如果用key表示超级节点关键码集，child表示子节点引用集，有

这样我们可以通过节点关键码对应的下标访问他的子节点

类似下图结构

两个序列直接用vector实现即可

代码如下：

#ifndef LXRBTNODE_H_ #define LXRBTNODE_H_ #include "../01 lxrvector/lxrvector.h" #define lxrBTNodePosi(T) lxrBTNode<T>* template<typename T> class lxrBTNode{ public: lxrvector<T> keys; lxrvector<lxrBTNodePosi(T)> children; lxrBTNodePosi(T) parent; lxrBTNode() {children.push_back(nullptr);} lxrBTNode(T const &key,lxrBTNodePosi(T) left=nullptr,lxrBTNodePosi(T) right=nullptr){ keys.push_back(key); children.push_back(left); children.push_back(right); } }; #endif

B-树的上溢-裂点

进行一次插入操作后，如果某个超级结点的分支数超过了该B树固定的分支数，就会引发上溢异常。在这种情况下，就需要对B树进行上溢调整。

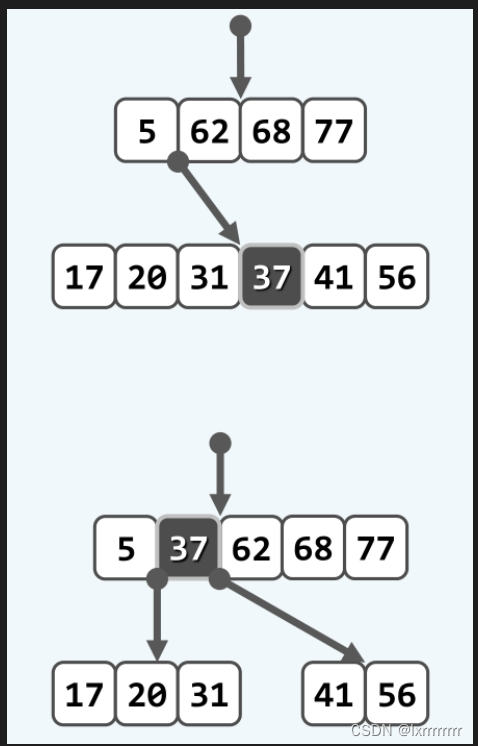
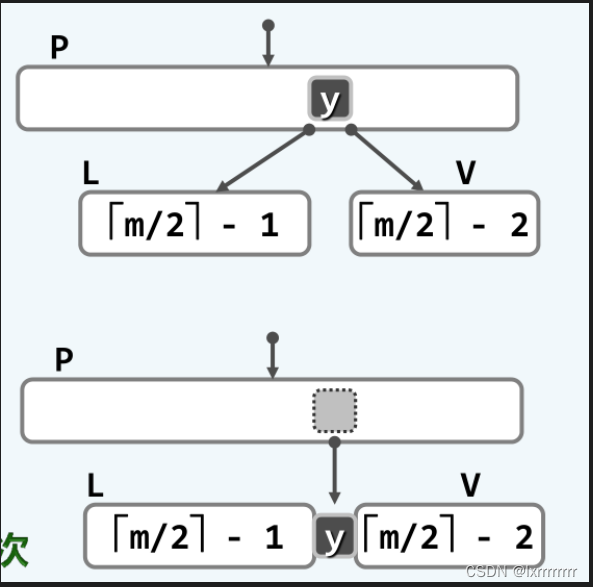
上溢调整的主要思路是分裂，即将一个上溢的超级结点分裂成两个较小的超级结点，这样该结点的父结点就会增加一个分支，从而需要添加一个关键码以维持结点数与分支数的平衡。可以选择上溢的结点的中间结点添加到父结点的关键码中，上溢结点以该关键码为界分裂成两个更小的超级结点。如下图所示：

需要注意的是，上溢调整后相当于原上溢结点的父结点也被插入了一个新的结点，因此该结点也可能因此产生上溢异常。通过这种方式，上溢可能会持续发生，并且不断地向上传播，直到传播至根结点。此时，应该将原根结点分裂，并且将中间结点提升为新的根结点，这也是B树高度增加的唯一方式。需要注意的是，此时根结点只具有两个分支，这也是B树定义中根结点的分支数不必遵守下限的原因。

上溢调整的具体代码如下：

//protected methods template <typename T> void lxrBTree<T>::solveOverflow(lxrBTNodePosi(T) x){ while(x->keys.getsize()==__order){ int mid= __order/2; lxrBTNodePosi(T) newLeaf=new lxrBTNode<T>(); lxrBTNodePosi(T) p=x->parent; //construct split node int ix=mid+1; newLeaf->children[0]=x->children[ix]; if(x->children[ix]) x->children[ix]->parent=newLeaf; for(;ix!=__order;++ix){ newLeaf->keys.push_back(x->keys[ix]); newLeaf->children.push_back(x->children[ix+1]); if(x->children[ix+1]) x->children[ix+1]->parent=newLeaf; } if(!p){//construct new_root __root=new lxrBTNode<T>(x->keys[mid],x,newLeaf); x->parent=__root; newLeaf->parent=__root; p=__root; } else{ int pos=p->keys.search(x->keys[mid]); p->keys.insert(pos+1,x->keys[mid]); p->children.insert(pos+2,newLeaf); newLeaf->parent=p; } x->keys.pop(mid,__order); x->children.pop(mid+1,__order+1); x=p; } }

B-树的下溢

与上溢异常相对应，当从B树中删除一个结点时，如果当前超级结点的分支数少于B树分支数的下限，就会产生下溢异常，此时需要对该结点进行下溢调整来恢复B树原本的性质。

下溢调整主要有两个策略。首要考虑的是左顾右盼，即产生下溢缺陷的结点首先去判断它的左右兄弟结点是否有多余的结点，如果的确有，那么可以从它的左右兄弟中借一个到当前产生下溢的结点中，这样下溢缺陷就可以修复。

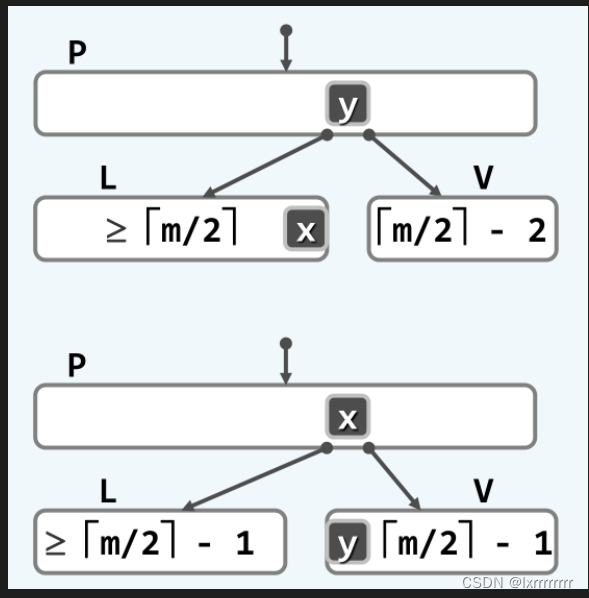
这里需要注意的是，实际借的结点并不是真的左右兄弟的结点，因为B树同时还要满足BST的局部有序性，所以实际上是左右兄弟的结点与父结点之间做了一个旋转，如下图所示：

借了这个结点后，被借的那个兄弟结点还需要将自己的一个子结点转让给下溢结点，才能使全树重新满足B树的性质。

可是，倘若左右兄弟结点都没有多余的关键码可借，就需要进行合并调整策略，这个过程其实就是上面分裂过程的逆过程。简单说来，就是将下溢结点，连同左/右结点中的一个，以及处于它们之间的父结点的关键码合并成为一个更大的超结点。具体的过程如下图所示：

可以证明，通过这种方式合并后产生的结点，一定是满足B树对结点的要求的。证明方法与上面分裂过程的证明一样。

需要注意的是，一次合并操作后，相当于从下溢结点的父结点也删除了一个关键码，从而其父结点相应的也有可能会产生下溢异常。因此，这种下溢异常可以不断地向上传播，直到传播至根结点。倘若唯一的根结点也产生下溢，那么全树的高度就会下降1，这也是B树高度降低的唯一原因。下溢调整过程的具体代码如下：

​ template <typename T> void lxrBTree<T>::solveUnderflow(lxrBTNodePosi(T) x){ while(x!=__root && x->children.getsize()==((__order-1)>>1)){ lxrBTNodePosi(T) p=x->parent; int pos=0; while(p->children[pos]!=x) ++pos; lxrBTNodePosi(T) leftSibling=(pos!=0 ? p->children[pos-1]:nullptr); lxrBTNodePosi(T) rightSibing=(pos!=p->children.getsize()-1 ? p->children[pos+1]:nullptr); //look around left and right if(leftSibling && leftSibling->children.getsize()>((__order+1)>>1)){ x->keys.insert(0,p->keys[pos-1]); x->children.insert(0,leftSibling->children.pop_back()); if(x->children[0]) x->children[0]->parent=x; p->keys[pos-1]=leftSibling->keys.pop_back(); return ; } else if(rightSibing && rightSibing->children.getsize()>((__order+1)>>1)){ x->keys.push_back(p->keys[pos+1]); x->children.push_back(rightSibing->children.pop(0)); if(x->children[x->children.getsize()-1]) x->children[x->children.getsize()-1]->parent=x; p->keys[pos+1]=rightSibing->keys.pop(0); return ; } else{ if(leftSibling){//merge left sibling leftSibling->keys.push_back(p->keys[pos-1]); int ix=0; for(;ix!=x->keys.getsize();++ix){ leftSibling->keys.push_back(x->keys[ix]); leftSibling->children.push_back(x->children[ix]); if(x->children[ix]) x->children[ix]->parent=leftSibling; p->keys.pop(pos-1); p->children.pop(pos); delete x; } } else{//merge right sibling x->keys.push_back(p->keys[pos]); int ix=0; for(;ix!=rightSibing->keys.getsize();++ix){ x->keys.push_back(rightSibing->keys[ix]); x->children.push_back(rightSibing->children[ix]); if(rightSibing->children[ix]) rightSibing->children[ix]->parent=x; } x->children.push_back(rightSibing->children[ix]); if(rightSibing->children[ix]) rightSibing->children[ix]->parent=x; p->keys.pop(pos); p->children.pop(pos+1); delete rightSibing; } if(p==__root && p->keys.getsize()==0){ __root=p->children[0]; __root->parent=0; p=__root; } x=p; } } } ​

函数总览

template <typename T> class lxrBTree{ protected: lxrBTNodePosi(T) __root; lxrBTNodePosi(T) __hot; int __order=3; int __size =0; //protected methods void solveOverflow(lxrBTNodePosi(T) x); void solveUnderflow(lxrBTNodePosi(T) x); public: //constructor lxrBTree() {__root=new lxrBTNode<T>();} lxrBTree(int order) : __order{order} {__root=new lxrBTNode<T>();} //public interfaces int getsize() {return __size;} lxrBTNodePosi(T) root() {return __root;} lxrBTNodePosi(T) search(T const &key); bool insert(T const &key); bool remove(T const &key); };

__order为B-树的阶数

search

B树的查找本质上和BST的查找没什么区别，

逐层搜索，如果在此超级节点命中即返return

如果不命中，pos将停留在最后一个小于key的元素，此时访问此超级节点的child中pos+1，即使key可能所在的下一层子节点

如此往复继续查找

注意这里keys.search的search是vector中的search

代码如下

template <typename T> lxrBTNodePosi(T) lxrBTree<T>::search(T const &key){ lxrBTNodePosi(T) x=__root; __hot=nullptr; int pos; while(x){ pos=x->keys.search(key); if(pos!=-1 && x->keys[pos]==key) break; __hot=x; x=x->children[pos+1]; } return x; }

insert

B树插入首先还是进行常规的插入操作，即无论是否会产生溢出，都首先将目标关键码插入到对应的超级结点中，随后再调用上面的`solveOverflow`方法对可能出现的上溢进行调整。

代码如下：

template <typename T> bool lxrBTree<T>::insert(T const &key){ lxrBTNodePosi(T) x=search(key); if(x) return false; x=__hot; int pos=x->keys.search(key); x->keys.insert(pos+1,key); x->children.push_back(nullptr); ++__size; solveOverflow(x); return true; }

remove

B树的删除就比较复杂了。首先肯定还是先在目标关键码所在的超级结点中删除掉目标关键码，之后再调用上面的`solveUnderflow`方法进行可能出现的下溢调整操作。

对于目标关键码的删除还是要分情况讨论：

如果目标关键码所在的超级结点是叶结点，那么就可以直接删除，注意不要忘了同时也删除掉该超级结点的一个分支。

如果目标关键码没有在叶结点中，类似BST的删除，还是需要先找到该关键码的直接后继。只是这里不同的是，只要该结点不是叶结点，那么该结点一定拥有右孩子（多路平衡搜索树），因此只需要从该结点的右孩子不断向左，即可找到该关键码的后继，从而转而删除它的后继关键码。

代码如下;

template <typename T> bool lxrBTree<T>::remove(T const &key){ lxrBTNodePosi(T) x=search(key); if(!x) return false; int pos=x->keys.search(key); if(x->children[0]){//if x not a leaf node lxrBTNodePosi(T) succ=x->children[pos+1]; while(succ->children[0]) succ=succ->children[0]; x->keys[pos]=succ->keys[0]; x=succ; pos=0; } //now x is a leaf node x->keys.pop(pos); x->children.pop_back(); --__size; solveUnderflow(x); return true; }

代码：

#ifndef LXRBTREE_H_ #define LXRBTREE_H_ #include "lxrBTNode.h" template <typename T> class lxrBTree{ protected: lxrBTNodePosi(T) __root; lxrBTNodePosi(T) __hot; int __order=3; int __size =0; //protected methods void solveOverflow(lxrBTNodePosi(T) x); void solveUnderflow(lxrBTNodePosi(T) x); public: //constructor lxrBTree() {__root=new lxrBTNode<T>();} lxrBTree(int order) : __order{order} {__root=new lxrBTNode<T>();} //public interfaces int getsize() {return __size;} lxrBTNodePosi(T) root() {return __root;} lxrBTNodePosi(T) search(T const &key); bool insert(T const &key); bool remove(T const &key); }; //protected methods template <typename T> void lxrBTree<T>::solveOverflow(lxrBTNodePosi(T) x){ while(x->keys.getsize()==__order){ int mid= __order/2; lxrBTNodePosi(T) newLeaf=new lxrBTNode<T>(); lxrBTNodePosi(T) p=x->parent; //construct split node int ix=mid+1; newLeaf->children[0]=x->children[ix]; if(x->children[ix]) x->children[ix]->parent=newLeaf; for(;ix!=__order;++ix){ newLeaf->keys.push_back(x->keys[ix]); newLeaf->children.push_back(x->children[ix+1]); if(x->children[ix+1]) x->children[ix+1]->parent=newLeaf; } if(!p){//construct new_root __root=new lxrBTNode<T>(x->keys[mid],x,newLeaf); x->parent=__root; newLeaf->parent=__root; p=__root; } else{ int pos=p->keys.search(x->keys[mid]); p->keys.insert(pos+1,x->keys[mid]); p->children.insert(pos+2,newLeaf); newLeaf->parent=p; } x->keys.pop(mid,__order); x->children.pop(mid+1,__order+1); x=p; } } template <typename T> void lxrBTree<T>::solveUnderflow(lxrBTNodePosi(T) x){ while(x!=__root && x->children.getsize()==((__order-1)>>1)){ lxrBTNodePosi(T) p=x->parent; int pos=0; while(p->children[pos]!=x) ++pos; lxrBTNodePosi(T) leftSibling=(pos!=0 ? p->children[pos-1]:nullptr); lxrBTNodePosi(T) rightSibing=(pos!=p->children.getsize()-1 ? p->children[pos+1]:nullptr); //look around left and right if(leftSibling && leftSibling->children.getsize()>((__order+1)>>1)){ x->keys.insert(0,p->keys[pos-1]); x->children.insert(0,leftSibling->children.pop_back()); if(x->children[0]) x->children[0]->parent=x; p->keys[pos-1]=leftSibling->keys.pop_back(); return ; } else if(rightSibing && rightSibing->children.getsize()>((__order+1)>>1)){ x->keys.push_back(p->keys[pos+1]); x->children.push_back(rightSibing->children.pop(0)); if(x->children[x->children.getsize()-1]) x->children[x->children.getsize()-1]->parent=x; p->keys[pos+1]=rightSibing->keys.pop(0); return ; } else{ if(leftSibling){//merge left sibling leftSibling->keys.push_back(p->keys[pos-1]); int ix=0; for(;ix!=x->keys.getsize();++ix){ leftSibling->keys.push_back(x->keys[ix]); leftSibling->children.push_back(x->children[ix]); if(x->children[ix]) x->children[ix]->parent=leftSibling; p->keys.pop(pos-1); p->children.pop(pos); delete x; } } else{//merge right sibling x->keys.push_back(p->keys[pos]); int ix=0; for(;ix!=rightSibing->keys.getsize();++ix){ x->keys.push_back(rightSibing->keys[ix]); x->children.push_back(rightSibing->children[ix]); if(rightSibing->children[ix]) rightSibing->children[ix]->parent=x; } x->children.push_back(rightSibing->children[ix]); if(rightSibing->children[ix]) rightSibing->children[ix]->parent=x; p->keys.pop(pos); p->children.pop(pos+1); delete rightSibing; } if(p==__root && p->keys.getsize()==0){ __root=p->children[0]; __root->parent=0; p=__root; } x=p; } } } //public interfaces template <typename T> lxrBTNodePosi(T) lxrBTree<T>::search(T const &key){ lxrBTNodePosi(T) x=__root; __hot=nullptr; int pos; while(x){ pos=x->keys.search(key); if(pos!=-1 && x->keys[pos]==key) break; __hot=x; x=x->children[pos+1]; } return x; } template <typename T> bool lxrBTree<T>::insert(T const &key){ lxrBTNodePosi(T) x=search(key); if(x) return false; x=__hot; int pos=x->keys.search(key); x->keys.insert(pos+1,key); x->children.push_back(nullptr); ++__size; solveOverflow(x); return true; } template <typename T> bool lxrBTree<T>::remove(T const &key){ lxrBTNodePosi(T) x=search(key); if(!x) return false; int pos=x->keys.search(key); if(x->children[0]){//if x not a leaf node lxrBTNodePosi(T) succ=x->children[pos+1]; while(succ->children[0]) succ=succ->children[0]; x->keys[pos]=succ->keys[0]; x=succ; pos=0; } //now x is a leaf node x->keys.pop(pos); x->children.pop_back(); --__size; solveUnderflow(x); return true; } #endif

今天的文章
北大数据结构与算法B课程作业_北大数据结构与算法附录B分享到此就结束了，感谢您的阅读。