目录

折半插入排序原理

折半插入排序图文说明

代码实现

C实现

 JAVA实现

 复杂度分析和稳定性

复杂度

稳定性

总结

折半插入排序原理

折半插入排序是对直接插入排序的一种改良方式，在直接插入排序中，每次向已排序序列中插入元素时，都要去寻找插入元素的合适位置，但是这个过程是从已排序序列的最后开始逐一去比较大小的，这其实很是浪费，因为每比较一次紧接着就是元素的移动。折半排序就是通过折半的方式去找到合适的位置，然后一次性进行移动，为插入的元素腾出位置。什么是折半的方式去找合适的位置呢，那就是折半查找了，因为再已排序的序列中，序列元素都是按照顺序排列的，既然这样，完全不需要逐一去比较大小，而是去比较已排序序列的中位数，这个中间的位置将一排序列分为左右两部分，通过一次比较后，就缩小了比较的范围，重复这样的操作，需要插入的元素就找到了合适的位置了。

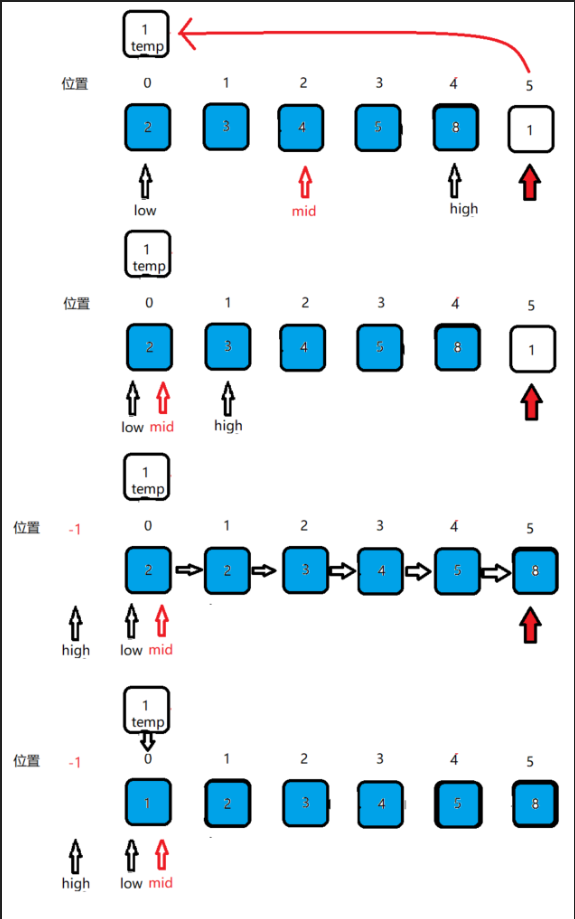
折半插入排序图文说明

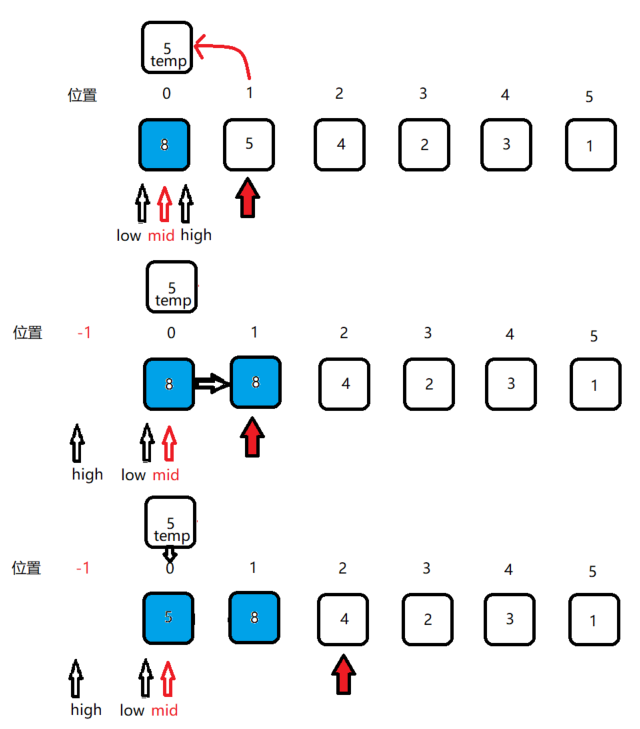
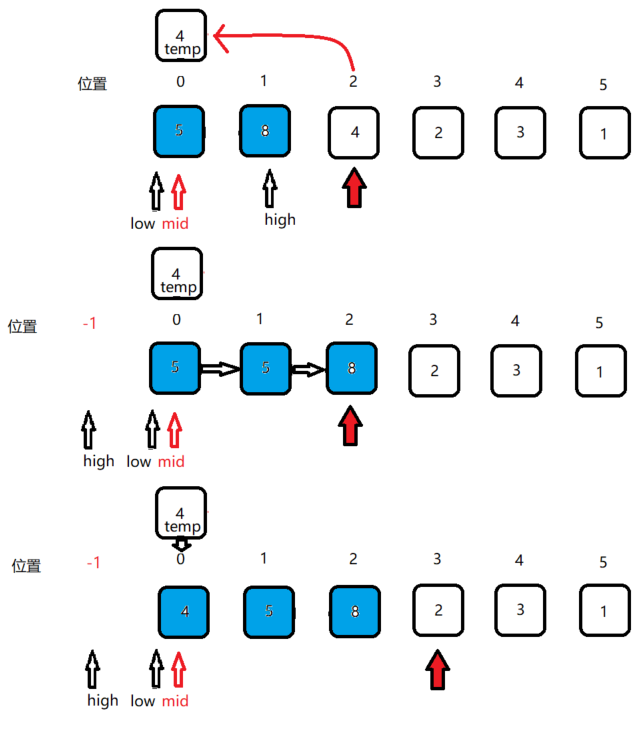
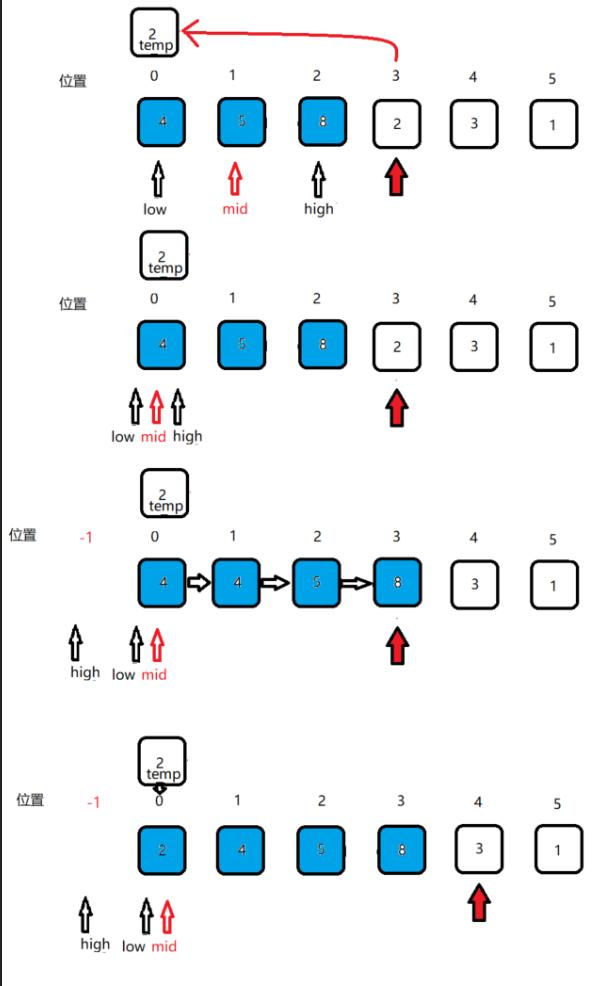
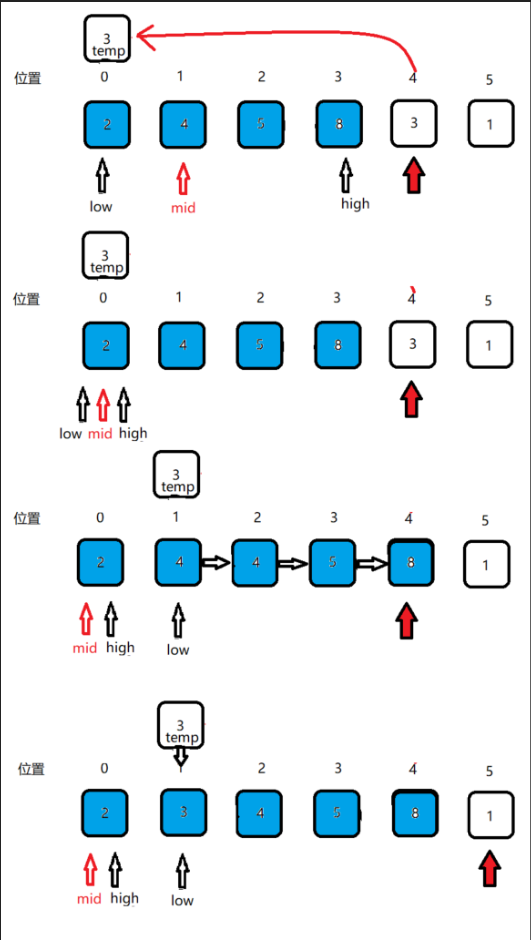
注：蓝色代表已排序序列，白色代表未排序序列，红色箭头指向未排序序列的第一个元素位置。

如图所示，现在有一个待排序序列[8 5 4 2 3]，首先默认初始状态下，位置0的数字8作为已排序序列[8]，位置1–位置4的[5 4 2 3 1] 为待排序序列，之后就逐一从[5 4 2 3 1]中取出数字向前进行比较，插入到已排序序列的合适位置。寻找过程中将蓝色的已排序区域不断进行折半。

初始状态下，已排序区只有一个数据元素8，low位置和high位置都指向了该位置，mid为中间位置，此时很显然也是0位（0+0）/ 2。此时temp < mid，将high指向mid的前一位，这里也就是-1，这个时候high=-1，low=1，很显然high<low，每当这个时候，就到了移动元素的时候了，将(high+1)到(i-1)的元素都向后移一位，再把（high+1）位置上插入要插入的元素。

之后的操作也是这样类似的，详细过程如下图。

代码实现

C实现

代码：

#include <stdio.h>
 
void insertSort(int array[], int n){
	int temp;

    for(int i = 1; i < n; i++){
         int low = 0;
         int hight = i-1;
         temp = array[i];

         while(hight>=low){
             int mid = ( low + hight ) / 2;
             if (array[mid] > temp){
                    hight = mid - 1;
             }else{
                 low = mid + 1;
              }
          }

          for (int j = i-1; j > hight; j--) {
              array[j+1] = array[j];
          }

          array[hight+1] = temp;
	}
}
 
void main(){
	int i;
	int a[8] = { 8, 5, 4, 3, 2, 1, 6, 7 };
 
	printf("before:{");
	for(i = 0; i < 8; i++){
		printf("%d ",a[i]);
	}
	printf("}\n");
 
	insertSort(a,8);
	
	printf("after:{");
	for(i = 0; i < 8; i++){
		printf("%d ",a[i]);
	}
	printf("}\n");
 
}

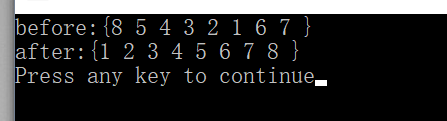
测试结果： 

 JAVA实现

代码：

/**
 * Created by GFC on 2018/8/29.
 */
public class HalfSearchSort {

    public void sort(int[] array){
        int temp;

        for(int i = 1; i < array.length; i++){
            int low = 0;
            int hight = i-1;
            temp = array[i];

            while(hight>=low){
                int mid = ( low + hight ) / 2;
                if (array[mid] > temp){
                    hight = mid - 1;
                }else{
                    low = mid + 1;
                }
            }

            for (int j = i-1; j > hight; j--) {
                array[j+1] = array[j];
            }

            array[hight+1] = temp;

        }

    }

    public static void main(String[] args) {
        HalfSearchSort sort = new HalfSearchSort();
        int a[] = {8, 5, 4, 3, 2, 1, 6, 7};

        System.out.println("Before: " + Arrays.toString(a));
        //System.out.println(5/2);
        sort.sort(a);
        System.out.println("After: " + Arrays.toString(a));
    }
}

 测试结果：

 复杂度分析和稳定性

复杂度

和直接插入排序相比较，折半插入排序仅仅是减少了比较的次数，而移动总次数并没有发生改变。这个比较次数大概是，移动次数没有改变，所以其复杂度和直接插入排序是一样的。

稳定性

根据代码分析可以知道，当待插入数与mid位置的值相等时，接下来相当于进入了有序序列的右半区，mid+1到high，之后经过多次折半查找，该元素所找到的合适位置就是前一个与之相等元素的后一位，所以说两者相对位置没有发生变化，这般插入排序是稳定的。

总结

折半插入排序其实是在直接插入排序的基础上，结合了二分查找法的思想，顺序的二分查找替代了直接插入排序中遍历查找的过程，从而更快的能够确定待插入元素的位置，但是由于移动次数并没有发生改变，所以两者的时间复杂度相同。折半插入排序是稳定的，其时间复杂度为。

今天的文章【排序】折半插入排序分享到此就结束了，感谢您的阅读。