机器学习入门必知
这篇文章的东西比较杂且碎,但都是很重要的必知知识,磨刀不误砍柴工。
一、机器学习中的术语表达
输入空间和输出空间
每个输入都是一个实例x,每个实例x都由n个特征来描述,一般用向量描述,x=(x(1),x(2),…,x(n))T。
n个实例x1,x2,…,xn的集合称为输入空间(有时候也叫特征空间)。
输入空间中的每个输入对应的输出y1,y2,…,yn的集合称为输出空间。
举个例子,假如在预测房价的模型中,每个输入都是一个房子x,每个房子x由面积x(1)和楼层x(2)两个特征来描述,那么房子x1可以描述为这样的向量:x1=(x(1)=120m2,x(2)=3层)T,其房价y1=300w;房子x2可以描述为这样的向量:x2=(x(1)=89m2,x(2)=6层)T,其房价y2=200w。
训练集,验证集和测试集
训练集用来训练模型,相当于课本的作用;
验证集用来选择模型,相当于课后作业的作用;
测试集用来最终评估,相当于最终的考试。
机器学习范围太广,并没有统一的理论体系涵盖所有内容,只能从多个角度对机器学习进行分类。
二、分类
1 基本分类
监督学习
监督学习从有标注数据中学习预测模型,本质是学习输入输出的映射的统计规律。而数据的标注通常是人工给出的,所以称为监督学习。(下面会结合一个关于预测房价的例子来讲)
在监督学习中,每个输入都是一个实例x,由特征向量来表示这个x,描述x的特征个数决定了特征向量的维度(比如每个输入都是一个房子x,每个房子由楼层x(1),面积x(2)两个特征来描述,所以每个x其实都是一个二维向量,第一个房子x1,第二个房子x2…第n个房子xn的集合就是特征空间)。
每个输出都是一个y(比如第一个房子x1的房价为y1=100w)。
重点来了,监督学习的训练数据集T中的每个元素都是一个输入输出对,T={(x1,y1),(x2,y2),…,(xn,yn)},每个训练数据都是带有标注y的,也就是说训练数据集中的每个房子的房价都已经告诉你了,而我们的目的是预测一个没见过的房子的价格。那么下一步就是通过训练数据集T来学习一个模型,当遇到一个训练数据集中没有的x时,通过该模型预测一个输出y。
监督学习有三个主要应用
- 回归问题,此类问题的输入变量连续,输出变量也是连续的,例如预测房价问题;
- 分类问题,此类问题的输入变量可以是离散的,也可以是连续的,但输出变量一定是离散的,例如预测肿瘤良性或恶性的问题,输出只有良和恶两个离散值;
- 标注问题,此类问题的输入和输出都是变量序列,例如词性标注问题。
无监督学习
可以很容易的想到,无监督学习就是从=无标注=的数据中学习预测模型。其本质是学习数据中的统计规律和潜在结构。它的训练数据集T中的每个元素并不是输入输出对,只有输入x。当遇到缺乏先验知识,人工标注太难或成本太高时,就可以来考虑考虑无监督学习了。
无监督学习最常用在聚类、降维中。
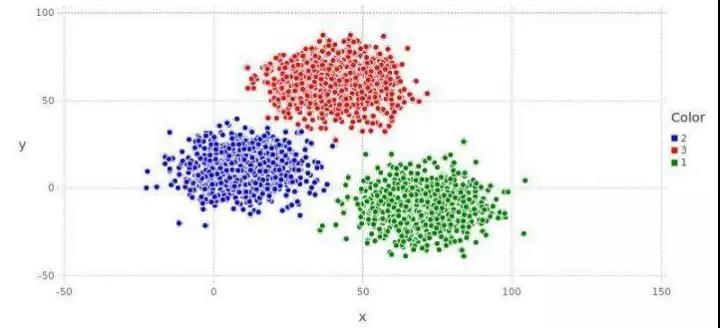
假如给出一堆数据,要学习它的潜在规律,学习之后,电脑发现某一堆点有共同的特征,便把它们归成一类,这便是聚类,如下图。
聚类又可以分为硬聚类和软聚类,硬聚类中的每个输入x只会被归为某一类,软聚类中的输入x有可能会被归为多类。
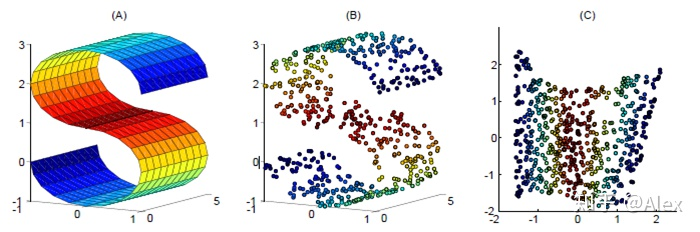
在机器学习中,并不是每个特征都对最后的结果有贡献,把没用的特征去掉,就是对特征空间进行降维,还降低了计算量。无监督学习用在降维中最常见的应用就是图像压缩,如下图,从第一张高清的s经过降维后转换成第二张,并不妨碍我们从第二张认出来它是个s,还降低了存储空间。
关于无监督学习的常用算法有:
等距映射法,局部线性嵌入法,拉普拉斯特征映射法,黑塞局部线性嵌入法,局部切空间排列法等
强化学习
强化学习是指智能系统在与环境的连续互动中学习最优行为策略。比如一个机器人要学习如何走到大门,当它走了一步离大门更近时,给它一个奖励,当它走了一步离大门更远了,便不给它奖励,为了得到更多的奖励,机器人最终会得到一条走到大门的最佳路线。
在强化学习中,智能系统不断地试错,它的目标不是短期奖励的最大化,而是长期累积奖励的最大化。比如阿尔法狗,它走当下这一步或许得到的奖励不是最大,但它通过计算知道下一步它会得到超级大的奖励,那么为了追求长期累积奖励的最大化,阿尔法狗会选择在目前来看并不是奖励最大的行为。
强化学习经常用在不需要进行一次决策的情形中,决策的量变才会引起结果的质变,关键的地方在于如何定义什么是应该奖励的行为,什么是应该惩罚的行为。
半监督学习
半监督学习的数据集通常有少量有标注,大量无标注,利用无标注的数据来辅助有标注数据,进行学习,以较低的成本达到较好的学习效果。
主动学习
主动学习是指机器不断主动给出实例让教师进行标注。
例如我们在刷小视频时,如果看到一条不喜欢的视频,我们可以将视频选成“不感兴趣”,之后app就会减少推送此类视频给你,在这里你相当于教师,你主动标注了你不喜欢的视频。
监督学习中的标注数据往往是随机得到的,可以看作是“被动学习”。
2 按模型分类
概率模型和非概率模型
概率模型在监督学习中是条件概率分布形式,比如“女生各个年龄段的身高模型”,预测18岁的女生身高是多少?模型并不是直接给出一个答案,而是从“18岁女生身高为163cm的概率=0.4,为168的概率=0.2,为170cm的概率=0.1”,从类似这样的概率分布中得到概率最大的身高为163cm,并把它作为答案输出。
非概率模型在监督学习中是函数f(x)的形式,比如输入一个女生的年龄=20岁,直接输出一个y=166cm。
概率模型的例子:决策树、朴素贝叶斯、隐马尔可夫模型、条件随机场、概率潜在语义分析、潜在迪利克雷分配、高斯混合模型;
非概率模型的例子:感知机、支持向量机、k近邻、AdaBoost、k均值、潜在语义分析、神经网络;
既可以看作概率模型也可看作非概率模型的例子:逻辑斯谛回归。
线性模型和非线性模型
特别的,对于非概率模型来说,如果函数是线性的,就是线性模型,否则就是非线性模型。
线性模型的例子:感知机、线性支持向量机、k近邻、k均值、潜在语义分析;
非线性模型的例子:核函数支持向量机、AdaBoost、神经网络。现在大火的深度学习其实就是学习复杂的非线性模型。
参数化模型和非参数化模型
模型是有参数的,参数化模型的参数固定或有限。非参数化模型的参数不固定或无限。
参数化模型的例子:感知机、朴素贝叶斯、逻辑斯谛回归、k均值、高斯混合模型、潜在语义分析、概率潜在语义分析、潜在迪利克雷分配;
非参数化模型的例子:决策树、支持向量机、AdaBoost,k近邻。
3 按算法分类
在线学习
一次只接受一个样本,进行预测,然后学习模型,不断重复。当遇到数据无法存储、数据规模太大无法一次性处理、数据模式不断动态变化等情况时,最好用在线学习。比如采用随机梯度下降的感知机学习算法就是在线学习。
批量学习
一次接受所有样本,学习模型,之后进行预测。
深度学习常用的一种方法是一次接受部分样本。
三、机器学习三要素
1 模型
机器学习第一个要考虑的问题就是要学习什么样的模型。
此处引入假设空间的重要概念,模型的假设空间包含所有可能的条件概率分布或函数。例如,假设函数是f(x)=ax时,假设空间就是a的所有可能取值对应的所有f(x)的函数集合。假设函数是f(x)=ax2+bx时,假设空间就是a和b的所有可能取值对应的所有f(x)的函数集合。
所以我们首要考虑的问题就是,对于每一个具体问题,应该选择哪种假设函数?
2 策略
假设函数选出来后,假设空间随之确定,下一个要考虑的问题就是按照什么样的策略来挑一个最优的模型
结构风险最小化策略
最常用的是结构风险最小化策略,下面来一步步得出这个策略。
-
损失函数和风险函数
损失函数度量模型一次预测的好坏;“好坏”说白了就是预测值和真实值的偏差。损失函数值越小,模型就越好,预测就越准确。
常用的损失函数有:0-1损失函数,平方损失函数,绝对损失函数,对数损失函数。
但一次预测并不能说明什么,我们要的是数据无穷大时的平均意义下的损失(联想微积分的思想)。
而风险函数度量的是模型平均意义下预测的好坏。这个平均意义下的损失也就是损失函数的期望,所以也称为期望损失。
此时期望损失最小的模型就是最优的模型。
但是在计算期望损失的过程中,需要知道联合分布P(X,Y),而该联合分布无法直接计算,此时便引出了经验风险的概念。 -
经验风险
经验风险是当前训练数据集的平均损失。
由于大数定理(不知道的自行百度),当样本量趋于无穷大时,平均损失(经验损失)=平均意义下的损失(期望损失),所以可以用经验风险来估计期望风险,此时经验损失最小的模型就是最优的模型。 -
经验风险最小化策略
该策略认为经验风险最小的模型就是最优的模型,当样本量足够大时,该策略有很好的效果,且当模型是条件概率分布模型,损失函数是对数损失函数时,经验风险最小化等价于极大似然估计。
然而当样本量很小时,用经验风险来估计期望风险并不理想,会出现过拟合现象。过拟合是一味追求对训练数据的预测能力,最终得到的模型参数过多,过于复杂,导致对训练数据拟合的很完美,对未知数据拟合的却很差。而我们追求的是对未知数据的拟合能力(称为泛化能力),所以引入了可以防止过拟合的结构风险最小化策略。 -
结构风险最小化策略
该策略认为结构损失最小的模型就是最优的模型。
结构损失就是在计算经验损失的基础上加了一个正则化项(也称罚项),该正则化项表示的是模型的复杂度,模型越复杂,该项越大,从而得到的结构损失越大,以此来平衡模型复杂度和拟合训练数据。
正则化符合奥卡姆剃刀原理,在所有可能选择的模型中,可以很好地拟合数据且十分简单的模型才是最好的模型。(从数学角度解释是KKT和拉格朗日)
交叉验证
-
简单交叉验证
该验证方法将数据分成两部分,大部分作为训练集,少部分作为测试集。
用训练集训练模型,用测试集评价各个模型的测试误差,最后选出测试误差最小的模型。
但此法只适用于数据足够的情况。 -
S折交叉验证
该验证方法将数据分成S份子集,每份有多个样本,然后用S-1个子集训练模型,用剩下的1个子集测试模型,每个模型如此循环重复测试S次,最后选出S次的平均测试误差最小的模型。
一表看懂:
| 分为3个子集 | 子集1 | 子集2 | 子集3 |
|---|---|---|---|
| 第一次验证 | 用来训练 | 用来训练 | 用来测试 |
| 第二次验证 | 用来训练 | 用来测试 | 用来训练 |
| 第三次验证 | 用来测试 | 用来训练 | 用来训练 |
- 留一交叉验证
该验证方法将数据分成S份子集,每份只有一个样本,相当于S折交叉的特殊情况。当数据非常缺乏时可以选择此验证方法。
3 算法
最后要考虑的问题就是用什么样的计算方法求解最优模型。
这时,机器学习问题转化为最优化问题,机器学习的算法转化为求解最优化问题的算法。一个好的求解算法既要保证找到全局最优解,也要保证求解过程十分高效。
参考李航老师的统计学习方法
今天的文章机器学习入门必知分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/62837.html