计算机博弈 基础算法 阿尔法-贝塔剪枝算法 α-β剪枝算法

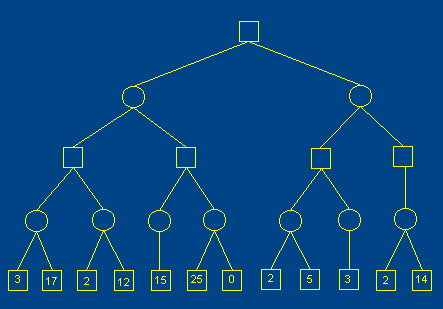
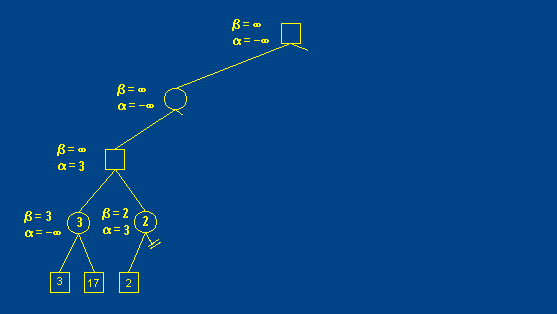
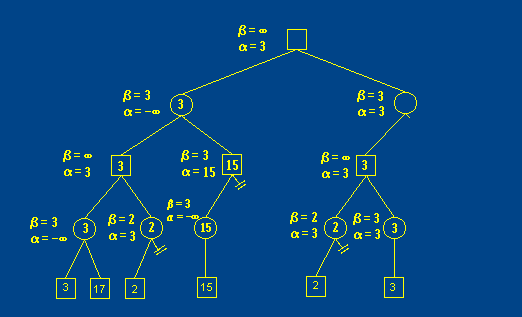
计算机博弈大赛中 α-β剪枝算法剪枝算法是极大极小算法的一种优化，可以更快的搜索博弈树

预备知识：
广度优先搜索(BFS)
深度优先搜索(DFS)
极大极小算法(MaxMin算法)

介绍
剪枝算法来源于极大极小算法，在博弈树分枝过多时可以使用这个方法有效的减少分支。因为在搜索到一定程度后，许多分支就没有了意义，那么这些无意义的分支就没必要进行搜索了。要使用剪枝算法，就必须确定从哪个方向开始搜索，一般使用从左到右。
例如，一个min层有3个节点，其父节点属于max层，其中一个min节点已经确定为值10，如果另一个min节点的子节点包含8，12，5点，那么当搜索到8节点后另外两个子节点就没有搜索的必要了。因为如果后面的节点大于8，那么min层的特性依然选择8；如果后面的节点小于8由min层父节点的特性可知，父节点只会选择10(10>8>可能的子节点)。同理，只要反过来思考即可推出max层的剪切方法。

图例：
初始设置α为负无穷大，β为正无穷大。



伪代码

// 初始a,b设为非常大的正数/负数
function minimax(node, depth, a, b)
    if node is a terminal node or depth = 0
        return the heuristic value of node
    if #opposite
        foreach child of node
            b = min(a, minimax(child, depth-1, a, b))
            if b <= a 
                  return b
        return b
    else we
        foreach child of node
            a = max(b, minimax(child, depth-1, a, b))
            if b <= a 
                   return a
         return a

今天的文章计算机博弈 基础算法 阿尔法-贝塔剪枝算法 α-β剪枝算法分享到此就结束了，感谢您的阅读。