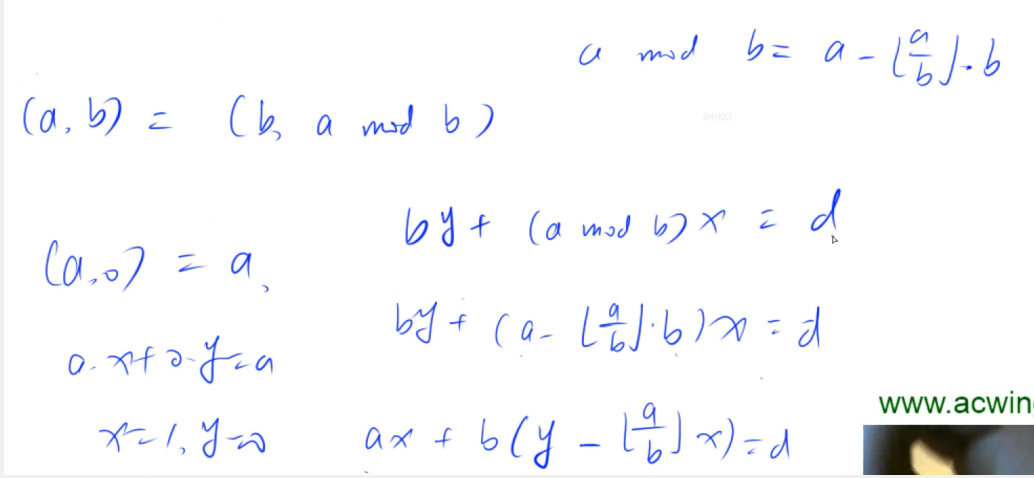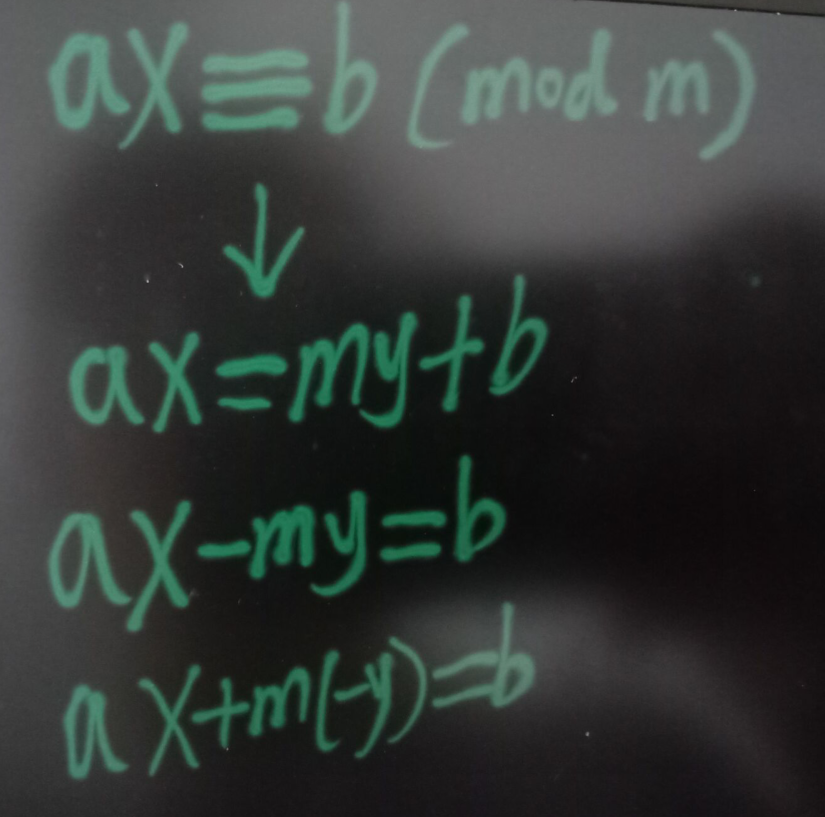这里证明不会讲解，因为写这篇文章的目的是为了让大家简单理解裴蜀定理。
以及可以在算法题中可以运用。主要针对于做题。

裴蜀定理(又称贝祖定理)

特殊性: 对于方程ax+by=1只有整数a和b互质时，方程才有整数解。

裴蜀定理的证明视频
裴蜀定理的证明文章

扩展欧几里德算法是用来在已知a , b 求解一组x , y ，使它们满足裴蜀（贝祖）等式： a x + b y = gcd ⁡ ( a , b ) = d

扩展欧几里得算法——exgcd

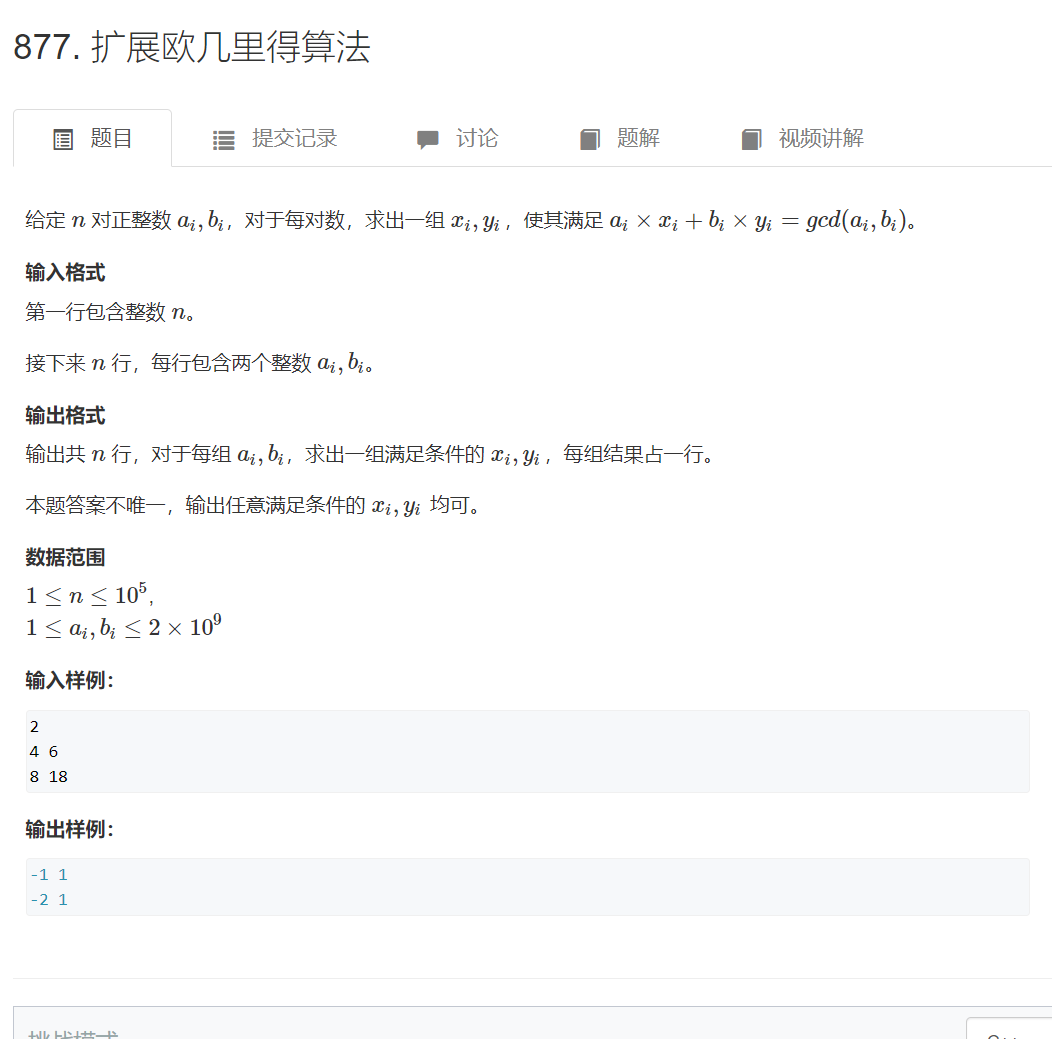
877. 扩展欧几里得算法

https://www.acwing.com/problem/content/description/879/

#include<cstdio>
#include<iostream>
using namespace std;
int exgcd(int a,int b,int &x, int &y)
{ 
   
    if(!b)
    { 
   
        x=1,y=0;
        return a;
    }
    int d=exgcd(b,a%b,y,x);
    y=y-a/b*x;
    return d;
}
int main(void)
{ 
   
    int t; cin>>t;
    while(t--)
    { 
   
        int a,b,x,y; cin>>a>>b;
        exgcd(a,b,x,y);
        cout<<x<<" "<<y<<endl;
    }
    return 0;
}

#include<bits/stdc++.h>
using namespace std;
int exgcd(int a,int b,int& x,int& y)
{ 
   
    if(!b) return x=1,y=0,a;
    int d=exgcd(b,a%b,y,x);
    y=y-a/b*x;
    return d;
}
int main(void)
{ 
   
    int n; cin>>n;
    while(n--)
    { 
   
        int a,b,x,y; cin>>a>>b;
        exgcd(a,b,x,y);
        cout<<x<<" "<<y<<endl;
    }
    return 0;
}

878. 线性同余方程

https://www.acwing.com/problem/content/880/

这不就是裴蜀定理么？ 我们知道1可以用扩展的欧几里得来求解。如同上面的是一样。
但是我们这里是 b。 我们可以先求 ax+my=gcd(a,m) 最后在乘以一个倍数就可以了。

我们平常求是这样的。

那么这里也是一样的我们求出一个x后再乘以一个数才为b即 X x b / gcd(a,m)
注意的是: b必须是gcd(a,m)的倍数，如果不是倍数，那么我们求x的过程中就会乘一个小数，那么x就不是整数了。
题目明确的给出 x 必须是整数。
结果得取m的模防止爆intax%m==(a*x%m)%m 故结果需要对m取模

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long int LL;
LL exgcd(LL a,LL b,LL &x,LL &y)
{ 
   
    if(!b){ 
   
        x=1,y=0;
        return a;
    } 
    int d=exgcd(b,a%b,y,x);
    y=y-a/b*x;
    return d;
}
int main(void)
{ 
   
    int t; cin>>t;
    while(t--)
    { 
   
        LL a,b,m; cin>>a>>b>>m;
        LL x,y,d;
        d=exgcd(a,m,x,y);
        if(b%d) cout<<"impossible"<<endl;
        else cout<<x*b/d%m<<endl;
    }
    return 0;
}

#include<bits/stdc++.h>
using namespace std;
typedef long long int LL;
LL exgcd(LL a,LL b,LL &x,LL &y)
{ 
   
    if(!b) return x=1,y=0,a;
    int d=exgcd(b,a%b,y,x);
    y=y-a/b*x;
    return d;
}
int main(void)
{ 
   
    int n; cin>>n;
    while(n--)
    { 
   
        LL a,b,m,x,y,d; cin>>a>>b>>m;
        d=exgcd(a,m,x,y);
        if(b%d) puts("impossible");
        else cout<<x*b/d%m<<endl;
    }
    return 0;
}

今天的文章裴蜀定理 【浅讲】分享到此就结束了，感谢您的阅读。