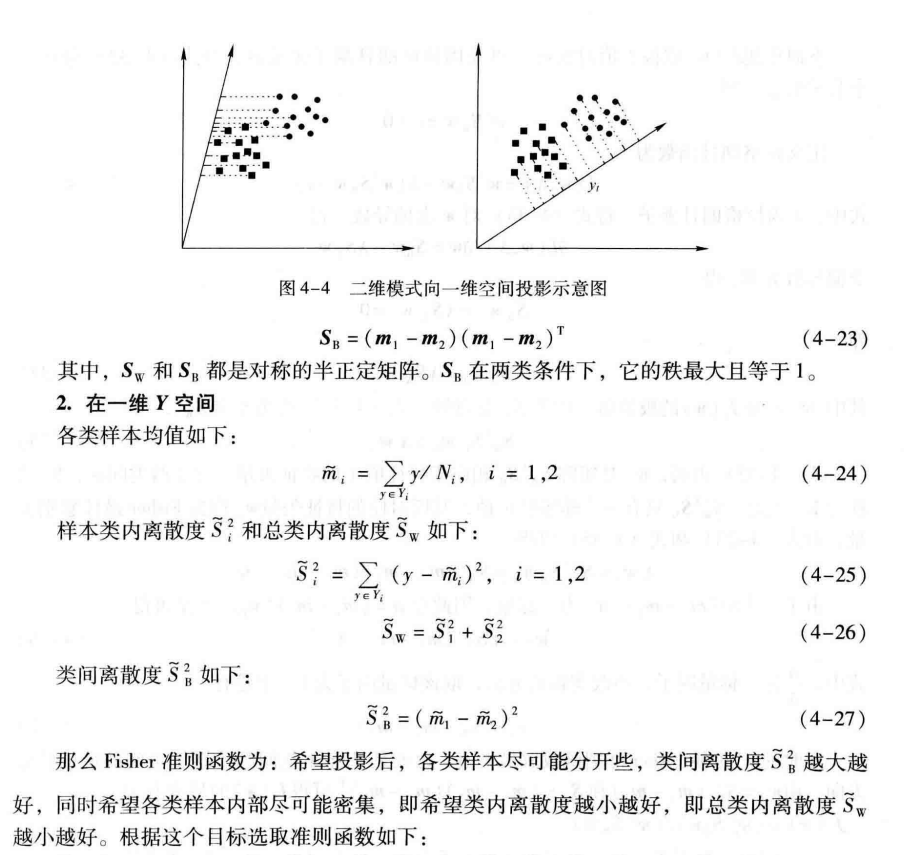
fisher线性判别原理_特征向量怎么求 例题

**

Fisher线性判别

**

【例4-1】本程序为纸币100元A面与50元A 面的Fisher判别门限的程序，通过全局变量 dat自动从样本数据中将内容读入dat[10][4][8][8][60]，dat为一个五维数组，第一维代表10 个样本，第二维代表人民币的币种，第三维代表旧版人民币的四个传感器数据和新

版人民币的四个传感器的数据，第四维代表八个传感器，第五维代表60次采样，程序将记录100元A面与50元A面各自的均值矢量、类内离差矩阵、类内离差总矩阵、投影特征向量和判别阈值。

//慰慰
double sw[32][8][8];//类内离差矩阵
double mj[32][8];//模式均值矢量
double sww[8][8];//类间离差矩阵
//fisher.cpp:Defines the entry point for the console application.//
//rmbdis.cpp:Defines the entry point for the console appication.//
#include"stdio.h"
#include"math.h"
#include"conio.h"
#include<fstream>
#include<iomanip>
using namespace std;
#define PNUM 60
unsigned char dat[10][4][8][8][60]={ 
   
//0--样本1，1--样本1，...，8--样本9，9--样本10
//0--100,1--50,2--20,3--10
//O--A向，1--B向，2--C向，3--D向，4--新版A向，5-新版B向，6--新版C向，7-新版D向
//0--传感1，1--传感2，2--传感3，3--传感4，4--传感5，5--传感6，6--传感7，7--传感8
{ 
   
#include"C:\\Users\\慰\\Desktop\\fisher线性判别\\样本\\rmb00.txt"
},
{ 
   
#include"C:\\Users\\慰\\Desktop\\fisher线性判别\\样本\\rmb01.txt"
},
{ 
   
#include"C:\\Users\\慰\\Desktop\\fisher线性判别\\样本\\rmb02.txt"
},
{ 
   
#include"C:\\Users\\慰\\Desktop\\fisher线性判别\\样本\\rmb03.txt"
},
{ 
   
#include"C:\\Users\\慰\\Desktop\\fisher线性判别\\样本\\rmb04.txt"
},
{ 
   
#include"C:\\Users\\慰\\Desktop\\fisher线性判别\\样本\\rmb06.txt"
},
{ 
   
#include"C:\\Users\\慰\\Desktop\\fisher线性判别\\样本\\rmb07.txt"
},
{ 
   
#include"C:\\Users\\慰\\Desktop\\fisher线性判别\\样本\\rmb08.txt"
},
{ 
   
#include"C:\\Users\\慰\\Desktop\\fisher线性判别\\样本\\rmb09.txt"
}
};
#define NUM 8
double Eueliden(double x[],double y[],int n)
{ 
   
double d;
d=0.0;
for(int i=0;i<n;i++){ 
   
d+=(x[i]-y[i])*(x[i]-y[i]);
}
d=sqrt(d);
return d;
}
double Manhattan(double x[],double y[],int n)
{ 
   
double d;
d=0.0;
for(int i=0;i<n;i++){ 
   
d+=fabs(x[i]-y[i]);
}
return d;
}

double Chebyshev(double x[],double y[],int n)
{ 
   
double d;
d=0.0;
for(int i=0;i<n;i++){ 
   
if(fabs(x[i]-y[i])>d)d=fabs(x[i]-y[i]);
}
return d;
}

double Minkowski(double x[],double y[],int n,int m)
{ 
   
double d;
d=0.0;
for(int i=0;i<n;i++){ 
   
d+=(double)powf((float)(x[i]-y[i]),(float)m);
}
d=(double)powf((float)d,1.0f/m);
return d;
}

double Mahalanobis(double x[],double y[],double matv1[8][8])
{ 
   
double dx,dy;
int i,j;

dx=0.0;
for(i=0;i<8;i++){ 
   
dy=0.0;
for(j=0;j<8;j++){ 
   
dy+=matv1[i][j]*(x[j]-y[j]);
}
dx+=dy*(x[i]-y[i]);
}
return dx;
}

void GetMatV(double V[8][8],int k)
{ 
   
int i,j,m,n1,n2,n3;
double xm[8],d,x,y;

m=4*8*PNUM;
for(i=0;i<8;i++){ 
   
d=0;
for(n1=0;n1<4;n1++){ 
   
for(n2=0;n2<8;n2++){ 
   
for(n3=0;n3<PNUM;n3++){ 
   
d+=(double)dat[k][1][n2][i][n3];
}
}
}
d/=m;
xm[i]=d;
}
for(i=0;i<8;i++){ 
   
for(j=0;j<8;j++){ 
   
d=0;
for(n1=0;n1<4;n1++){ 
   
for(n2=0;n2<8;n2++){ 
   
for(n3=0;n3<PNUM;n3++){ 
   
x=(double)dat[k][n1][n2][i][n3]-xm[i];
y=(double)dat[k][n1][n2][j][n3]-xm[j];
d+=x*y;
}
}
}
d/=m-1.0;
V[i][j]=d;
}
}
}

void Gauss_Jordan(double matv[8][8],double matv1[8][8])
{ 
   
int n=8;
double mat[8][16],d;
int i,j,l,k;
for(i=0;i<n;i++){ 
   
for(j=0;j<2*n;j++){ 
   
if(j<n)
mat[i][j]=matv[i][j];
else
mat[i][j]=0.0;
}
}
for(i=0;i<n;i++)mat[i][n+i]=1.0;
for(k=0;k<n;k++){ 
   
d=fabs(mat[k][k]);
j=k;
for(i=k+1;i<n;i++){ 
   
if(fabs(mat[i][k])>d){ 
   //选主元
d=fabs(mat[i][k]);
j=i;
}
}

if(j!=k){ 
   //交换
for(l=0;l<2*n;l++){ 
   
d=mat[j][l];
mat[j][l]=mat[k][l];
mat[k][l]=d;
}
}
for(j=k+1;j<2*n;j++){ 
   
mat[k][j]/=mat[k][k];
}
for(i=0;i<n;i++){ 
   
if(i==k)continue;
for(j=k+1;j<2*n;j++){ 
   
mat[i][j]-=mat[i][k]*mat[k][j];
}
}
}

for(i=0;i<n;i++){ 
   
for(j=0;j<n;j++){ 
   
matv1[i][j]=mat[i][j+n];
}
}
}

void getswj(double mats[8][8],double mj[8],unsigned char data[8][60])
{ 
   
int i,j,k;
for(i=0;i<8;i++){ 
   
mj[i]=0.0;
for(k=0;k<PNUM;k++){ 
   
mj[i]+=(double)data[i][k];
}
mj[i]/=60.0;
}
for(i=0;i<8;i++){ 
   
for(j=0;j<8;j++){ 
   
mats[i][j]=0;
for(k=0;k<PNUM;k++){ 
   
mats[i][j]+=(data[i][k]-mj[i])*(data[j][k]-mj[j]);
}
mats[i][j]/=59.0;
}
}
}

void get4sw(double mats[8][8],double mj[8],unsigned char data[8][8][60])
{ 
   
int i,j,k,m;
for(i=0;i<NUM;i++){ 
   
mj[i]=0.0;
for(j=0;j<8;j++){ 
   
for(k=0;k<PNUM;k++){ 
   
mj[i]+=(double)data[j][i][k];
}
}
mj[i]/=8.0*PNUM;
}
for(i=0;i<NUM;i++){ 
   
for(j=0;j<NUM;j++){ 
   
mats[i][j]=0;
for(m=0;m<8;m++){ 
   
for(k=0;k<PNUM;k++){ 
   
mats[i][j]+=(data[m][i][k]-mj[i])*(data[m][j][k]-mj[j]);
}
}
mats[i][j]/=8*PNUM-1;
}
}
}

void getsb(double sb[8][8],double mj[32][8],unsigned char data[4][8][8][60])
{ 
   
int i,j,k;
double m[8];
for(i=0;i<8;i++){ 
   
m[i]=0;
for(j=0;j<32;j++){ 
   
for(k=0;k<60;k++){ 
   
m[i]+=data[j/8][j%8][i][k];
}
}
m[i]/=60.0*32.0;
}
for(i=0;i<8;i++){ 
   
for(j=0;j<8;j++){ 
   
sb[i][j]=0;
for(k=0;k<32;k++){ 
   
sb[i][j]+=(mj[k][i]-m[i])*(mj[k][j]-m[j]);
}
sb[i][j]/=32;
}
}
}

void getsw(double swj[32][8][8],double sw[8][8])
{ 
   
int i,j,k;
for(i=0;i<8;i++){ 
   
for(j=0;j<8;j++){ 
   
sw[i][j]=0;
for(k=0;k<32;k++){ 
   
sw[i][j]+=swj[k][i][j];
}
sw[i][j]/=32.0;
}
}
}

void MatMul(double mata[8][8],double matb[8][8],double matc[8][8])
{ 
   
int i,j,k;
for(i=0;i<NUM;i++){ 
   
for(j=0;j<NUM;j++){ 
   
matc[i][j]=0;
for(k=0;k<NUM;k++){ 
   
matc[i][j]+=mata[i][k]*matb[k][j];
}
}
}
}

void MatAdd(double mata[8][8],double matb[8][8],double matc[8][8])
{ 
   
int i,j;
for(i=0;i<NUM;i++){ 
   
for(j=0;j<NUM;j++){ 
   
matc[i][j]=mata[i][j]+matb[i][j];
}
}
}

void MatDec(double mata[8][8],double matb[8][8],double matc[8][8])
{ 
   
int i,j;
for(i=0;i<NUM;i++){ 
   
for(j=0;j<NUM;j++){ 
   
matc[i][j]=mata[i][j]-matb[i][j];
}
}
}

void getst(double sw[8][8],double sb[8][8],double st[8][8])
{ 
   
MatAdd(sw,sb,st);
}
double MatTrace(double mat[8][8])
{ 
   
int i;
double d=0.0;

for(i=0;i<NUM;i++){ 
   
d+=mat[i][i];
}
return d;
}

void OutSw(ofstream outfile,double sw[NUM][NUM])
{ 
   
int i,j;
for(i=0;i<NUM;i++){ 
   
for(j=0;j<NUM;j++){ 
   
outfile<<setprecision(5)<<sw[i][j];
if(j<NUM-1)outfile<<",";
else outfile<<endl;
}
}
}
double MulVector(double x[NUM],double y[NUM])
{ 
   
int i;
double d;
d=0.0;
for(i=0;i<NUM;i++){ 
   
d+=x[i]*y[i];
}
return d;
}
int main(int argc,char*argv[])
{ 
   
double sw[32][8][8];
double mj[32][8];
double sww[8][8];
double sww1[8][8];
int i,j;
/*get4sw(sw[0],mj[0],dat[0][0]); get4sw(sw[8],mj[8],da[0][1]); get4sw(sw[16],mj[16],dat[0][2]); get4sw(sw[24],mj[24],dat[0][3]);*/
char name[20]="sw100a.h";
for(i=0;i<32;i++){ 
   
getswj(sw[i],mj[i],dat[0][i/8][i%8]);
}

MatAdd(sw[0],sw[8],sww);
Gauss_Jordan(sww,sww1);
ofstream outfile;
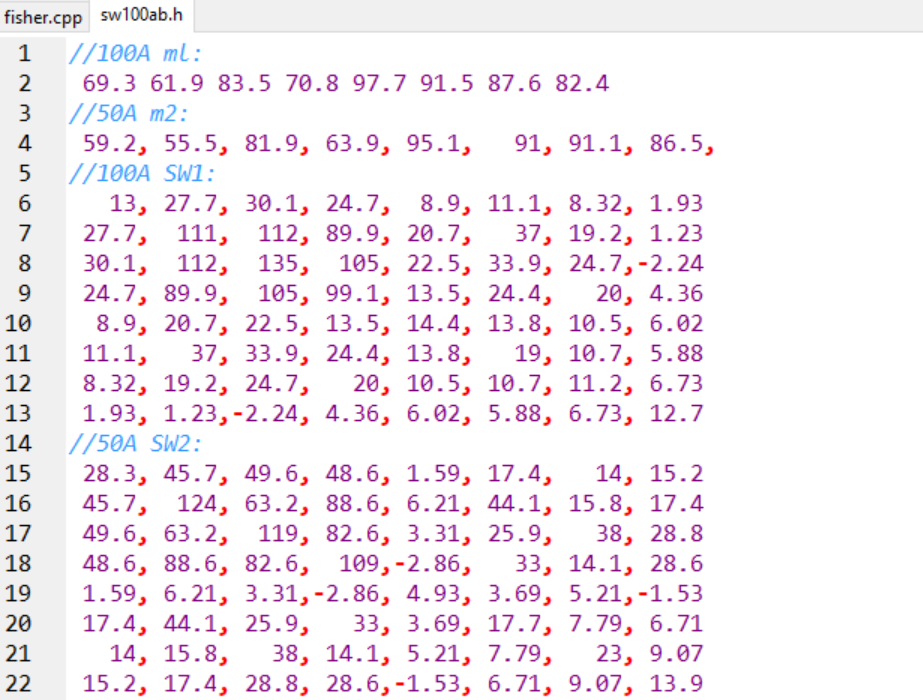
outfile.open("sw100ab.h");
outfile<<"//100A ml:\n";
for(i=0;i<NUM;i++){ 
   
outfile<<setw(5)<<setprecision(3)<<mj[0][i]<",";
}
outfile<<endl;
outfile<<"//50A m2:\n";
for(i=0;i<NUM;i++){ 
   
outfile<<setw(5)<<setprecision(3)<<mj[8][i]<<",";
}
outfile<<endl;
outfile<<"//100A SW1:\n";
for(i=0;i<NUM;i++){ 
   
for(j=0;j<NUM;j++){ 
   
outfile<<setw(5)<<setprecision(3)<<sw[0][i][j];
if(j<NUM-1)outfile<<",";
else outfile<<endl;
}
}
outfile<<"//50A SW2:\n";
for(i=0;i<NUM;i++){ 
   
for(j=0;j<NUM;j++){ 
   
outfile<<setw(5)<<setprecision(3)<<sw[8][i][j];
if(j<NUM-1)outfile<<",";
else outfile<<endl;
}
}
outfile<<"//SW=SW1＋SW2:\n";
for(i=0;i<NUM;i++){ 
   
for(j=0;j<NUM;j++){ 
   
outfile<<setw(5)<<setprecision(3)<<sww[i][j];
if(j<NUM-1)outfile<<",";
else outfile<<endl;
}
}
outfile<<"//SW-1:\n";
for(i=0;i<NUM;i++){ 
   
for(j=0;j<NUM;j++){ 
   
outfile<<setw(5)<<setprecision(3)<<sww1[i][j];
if(j<NUM-1)outfile<",";
else outfile<<endl;
}
}
double d,u[NUM];
for(i=0;i<NUM;i++){ 
   
d=0.0;
for(j=0;j<NUM;j++){ 
   
d+=sww1[i][j]*(mj[0][j]-mj[8][j]);
}
u[i]=d;
}
outfile<"//u=sw-1(ml-m2):\n";
for(i=0;i<NUM;i++){ 
   
outfile<<setw(5)<<setprecision(3)<<u[i]<<",";
}
outfile<<endl;
d=MulVector(u,mj[0]);
outfile<<"u*ml="<<d<<endl;
double d2;
d2=MulVector(u,mj[8]);
outfile<<"u*m2="<<d2<<endl;
d=(d+d2)/2.0;
outfile<<"yt="<<d<<endl;
double pt[NUM];
outfile<<"100AResult:\n";
for(i=0;i<PNUM;i++){ 
   
for(j=0;j<NUM;j++){ 
   
pt[j]=(double)dat[0][0][0][j][i];
}
d=MulVector(u,pt);
outfile<<setw(5)<<setprecision(3)<<d;
if((i+1)%8==0)
outfile<<endl;
else outfile<<",";
}
outfile<<endl;
outfile<<"50AResult:\n";
for(i=0;i<PNUM;i++){ 
   
for(j=0;j<NUM;j++){ 
   
pt[j]=dat[0][1][0][j][i];
}
d=MulVector(u,pt);
outfile<<setw(5)<<setprecision(3)<<d;
if((i+1)%8==0)outfile<<endl;
else outfile<<",";
}
outfile<<endl;
outfile.close();
return 0;
}

今天的文章fisher线性判别原理_特征向量怎么求 例题分享到此就结束了，感谢您的阅读。