多目标优化问题的算法及其求解

一、多目标优化问题

  多目标优化是在现实各个领域中都普遍存在的问题，每个目标不可能都同时达到最优，必须各有权重。但是，究竟要怎样分配这样的权重，这已经成为人们研究的热点问题。同时，根据生物进化论发展起来的遗传算法，也得到了人们的关注。将这两者结合起来，能够利用遗传算法的全局搜索能力，避免传统的多目标优化方法在寻优过程中陷入局部最优解，可以使解个体保持多样性。所以，基于遗传算法的多目标寻优策略已经被应用于各个领域中。

二、多目标优化的数学描述

  一般来讲，多目标优化问题是由多个目标函数与有关的一些等式以及不等式约束组成，从数学角度可以做如下描述：$$min{f}_1(x_1,x_2,...,x_n)$$$$............$$ $$min{f}_r(x_1,x_2,...,x_n)$$ $$max{f}_{r+1}(x_1,x_2,...,x_n)$$ $$............$$ $$max{f}_m(x_1,x_2,...,x_n)$$ $$s.t.g_i(x)\ge 0,i=1,2,...,p$$ $$h_j(x)\ge 0,j=1,2,...,q$$ (1)
  式中，函数 f i ( x ) , { i = 1 , 2 , 3 , . . . , m } f_i(x),\{i={1,2,3,…,m}\} fi​(x),{
i=1,2,3,...,m}称为目标函数；$g_i(x)$和$h_i(x)$称为约束函数； x = { x 1 , x 2 , . . . , x n } T x=\{x_1,x_2,…,x_n\}^T x={
x1​,x2​,...,xn​}T是$n$维的设计变量。 X = { x ∣ x ∈ R n , g i ( x ) ≥ 0 , h j ( x ) = 0 , i = 1 , 2 , . . . , p , j = 1 , 2 , . . . , q } X=\{x|x\in R^n,g_i(x)\ge0,h_j(x)=0,i=1,2,…,p,j=1,2,…,q\} X={
x∣x∈Rn,gi​(x)≥0,hj​(x)=0,i=1,2,...,p,j=1,2,...,q}称为上述公式的可行域。
  在这个多目标优化问题中有$m(m\ge 2)$个目标函数($r$个极小化目标函数，$(m-r)$个极大化目标函数)和$(p+q),p,q\ge 0$个约束函数(其中有$p$个不等式约束和$q$个等式约束)。
  如果上述多目标优化问题公式（1）的目标函数全部是极小化目标函数，约束函数全都是不等式约束，则可以得到一个标准多目标优化模型：$$minF(X)=[f_1(x),f_2(x),...,f_m(x){]}^T$$ $$s.t.g_i(x)\le 0,i=1,2,...,p$$(2)
  设计变量 x = { x 1 , x 2 , . . . , x n } T x=\{x_1,x_2,…,x_n\}^T x={
x1​,x2​,...,xn​}T是一组确定的向量，对应$n$维欧氏设计变量空间$R^n$上的一点，而相应的目标函数$f(x)$则对应一个$m$维的欧氏目标函数$R^m$空间的一点。也就是说，目标函数$f(x)$对应的是由n维设计变量空间到m维目标函数空间的一个映射：$$f:R^n\to R^m$$
  由此可知，设计变量、目标函数以及约束函数是构成多目标优化问题的三要素。
  设计变量$x_1,x_2,...,x_n$是在实际工程设计中可以人为指定控制的，并且能对工程系统的属性、性能产生影响的一组向量，不同取值的设计变量便意味着对应不同的工程系统设计方案，一组设计变量通常可以用向量 x = { x 1 , x 2 , . . . , x n } T x=\{x_1,x_2,…,x_n\}^T x={
x1​,x2​,...,xn​}T表示，并把它称之为优化问题的一个解。
  目标函数可以看作是评价设计系统性能指标的数学表达式，在实际工程设计中，设计者（决策者）希望能同时使这些性能指标达到最优化。所有的目标函数$f_1(x),f_2(x),...,f_m(x)$构成了多目标优化问题(2)的目标函数向量$F(X)$。
  约束条件给出了设计变量需要满足的限制条件，用含有等式和不等式的约束函数来表示。满足所有约束函数（约束条件）的一组设计变量可以称之为一个***可行解***，优化问题中所有的可行解构成了整个优化问题的可行域。

三、多目标优化的目标占优和Pareto占优

  在多目标优化算法的搜索中，普遍使用了占优(dominate)的概念。在这里将给出占优的概念以及相关术语的定义。

定义1：帕累托占优（Pareto Dominate）和帕累托最优解（Pareto Optimal）

  考察两个决策向量$a,b\in X$。$a$帕累托占优（Pareto Dominate）$b$,记为$a>b$,当且仅当： { ∀ i ∈ { 1 , 2 , . . . , n } f i ( a ) ≤ f i ( b ) } ∧ { ∃ j ∈ { 1 , 2 , . . . , n } f j ( a ) < f j ( b ) } \{\forall i\in \{1,2,…,n \}f_i(a)\le f_i(b)\} \land\{\exists j\in \{1,2,…,n \}f_j(a)<f_j(b)\} {
∀i∈{
1,2,...,n}fi​(a)≤fi​(b)}∧{
∃j∈{
1,2,...,n}fj​(a)<fj​(b)}
  如果在整个参数空间内不存在任何决策向量帕累托占优某个决策向量，则称该决策向量既是帕累托最优解。所有帕累托最优解组成了帕累托最优解集合（Pareto Optimal Set）。

定义2：绝对最优解、非劣解、帕累托前沿（Pareto Front）

   设S为多目标优化的可行域，$f(x)$为多目标优化的向量目标函数。
   若$f(X^{\ast })\le f(X)\forall X\in S$，则$f^{\ast }$称是多目标优化的***绝对最优解***。
  若$f(X)\le f(X^{-})\forall X\in S$，则称$X^{-}$是多目标优化问题的***非劣解***，即***Pareto最优解***。非劣解也成为有效解(Efficient Solution)、非支配解(Non-dominated Solution)、Pareto最优解(Pareto Optimal Solution)或Pareto解。
  多目标优化问题的非劣解一般不止一个，由所有非劣解构成的集合称为***非劣解集(Non-inferior Set)***。所有非劣解对应的目标函数构成了多目标优化问题的***非劣最优目标域***，也成为***Pareto前缘(Pareto Front)***，再不引起混淆的情况下也可以称为非劣解集。

四、多目标优化问题的解

  在单目标优化问题中，通常最优解只有一个，而且能用比较简单和常用的数学方法求出其最优解。然而在多目标优化问题中，各个目标之间相互制约，可能使得一个目标性能的改善往往是以损失其它目标性能为代价，不可能存在一个使所有目标性能都达到最优的解，所以对于多目标优化问题，其解通常是一个非劣解的集合——Pareto解集。
  在存在多个Pareto最优解的情况下，如果没有关于问题的更多的信息，那么很难选择哪个解更可取，因此所有的Pareto最优解都可以被认为是同等重要的。由此可知，对于多目标优化问题，最重要的任务是找到尽可能多的关于该优化问题的Pareto最优解。因而，在多目标优化中主要完成以下两个任务：

1)找到一组尽可能接近Pareto最优域的解。
2)找到一组尽可能不同的解。

  第一个任务是在任何优化工作中都必须的做到的，收敛不到接近真正Pareto最优解集的解是不可取的，只有当一组解收敛到接近真正Pareto最优解，才能确保该组解近似最优的这一特性。
  除了要求优化问题的解要收敛到近似Pareto最优域，求得的解也必须均匀稀疏地分布在Pareto最优域上。一组在多个目标之间好的协议解是建立在一组多样解的基础之上。因为在多目标进化算法中，决策者一般需要处理两个空间——决策变量空间和目标空间，所以解(个体)之间的多样性可以分别在这两个空间定义。例如，若两个个体在决策变量空间中的欧拉距离大，那么就说这两个解在决策变量空间中互异；同理，若两个个体在目标空间中的欧拉距离大，则说它们在目标空间中互异。尽管对于大多数问题而言，在一个空间中的多样性通常意味着在另一个空间中的多样性，但是此结论并不是对所有的问题都是成立的。对于这样复杂的非线性优化问题，要找到在要求的空间中有好的多样性的一组解也是一项非常重要的任务。

五、求解帕累托前沿解的方法

  目前求解帕累托前沿解的主要算法有基于数学的规划方法和基于遗传算法的两类方法。本文重点介绍目前使用较普遍的NSGA-II算法。
  多目标遗传算法是用来分析和解决多目标优化问题的一种进化算法，其核心就是协调各个目标函数之间的关系，找出使得各个目标函数都尽可能达到比较大的（或比较小的）函数值的最优解集。在众多多目标优化的遗传算法中，NSGA-II算法（带精英策略的非支配排序遗传算法(Elitist Non-Dominated Sorting Genetic Algorithm，NSGA-II)，NSGA-II ）是影响最大和应用范围最广的一种多目标遗传算法。在其出现以后，由于它简单有效以及比较明显的优越性，使得该算法已经成为多目标优化问题中的基本算法之一。该算法主要优点（改善内容）如下三点：

1. 提出了快速非支配的排序算法，降低了计算非支配序的复杂度，使得优化算法的复杂度由原来的$m{N}^3$降为$m{N}^2$（$m$为目标函数的个数，$N$为种群的大小）。
2. 引入了精英策略，扩大了采样空间。将父代种群与其产生的子代种群组合在一起，共同通过竞争来产生下一代种群，这有利于是父代中的优良个体得以保持，保证那些优良的个体在进化过程中不被丢弃，从而提高优化结果的准确度。并且通过对种群所有个体分层存放，使得最佳个体不会丢失，能够迅速提高种群水平。
3. 引入拥挤度和拥挤度比较算子，这不但克服了NSGA算法中需要人为指定共享参数$Shar{e}_{\sigma }$的缺陷，而且将拥挤度作为种群中个体之间的比较准则，使得准Pareto域中的种群个体能均匀扩展到整个Pareto域，从而保证了种群的多样性。
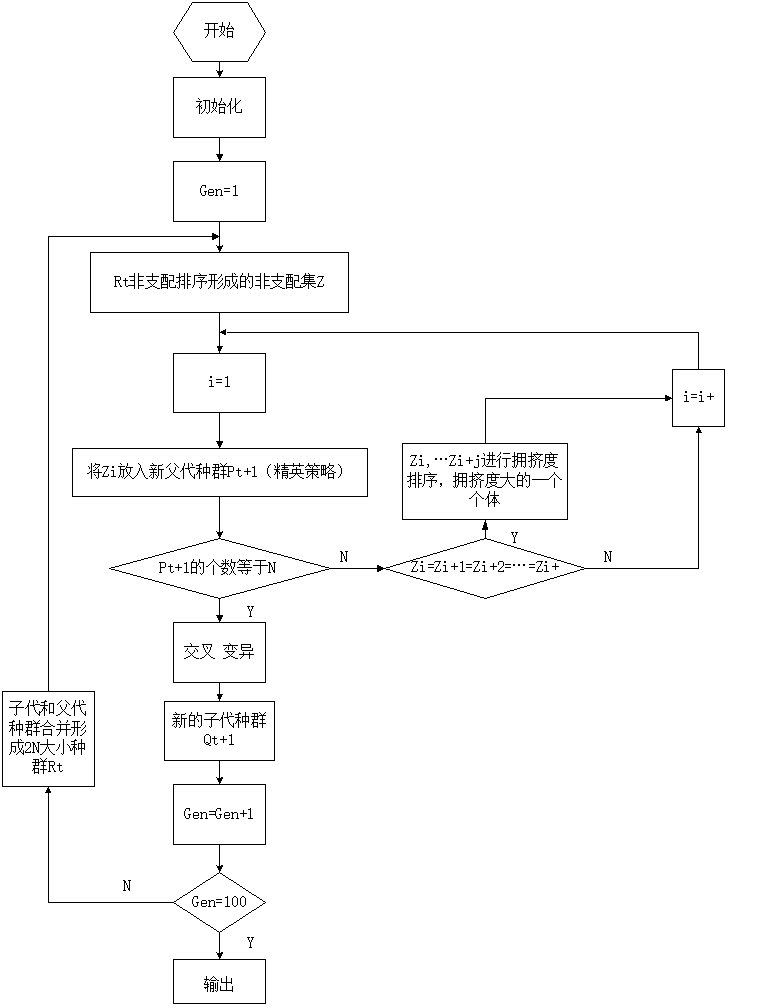
     NSGA-II算法流程图如下：
   

六、在供应链优化过程中的应用案例

  供应链系统优化问题的本质是：
1）供应链可以理解为一个多实体集成的系统或网络，它同步一系列相互关联的实体业务流程；
2）协同优化问题不是最大限度地提高单一实体的盈利能力，而是促进各种合作伙伴（包括供应商，制造商，零售商，分销商和第三方物流供应商）共同盈利能力；
3）只有当所有实体都希望优化整个供应链的性能和盈利能力（协同优化），并且不将其个体偏好（个体优化）置于系统的优先级之外时，才能实现协同优化；
4）供应链协同优化必须找到一种尽可能兼顾满足个体偏好，同时最大规模实现全局最优帕累托解的解决方案。
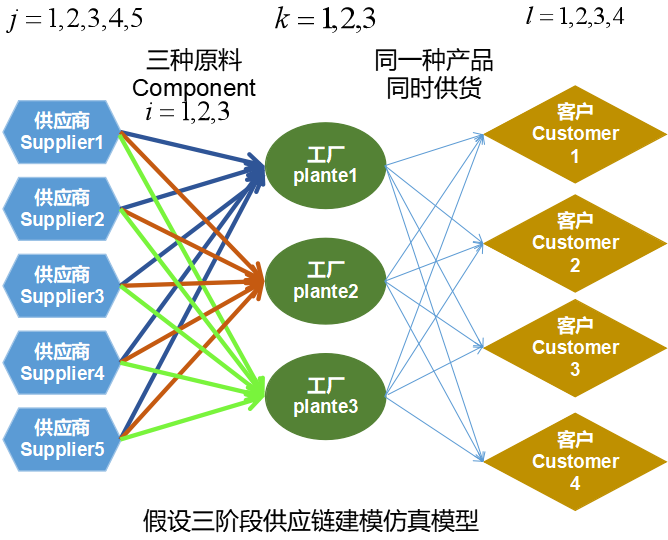
  假设如下供应链模型：

驱动数据集
(i, j): Component-Supplier 组件 – 供应商
(i, j, k): Component-Supplier-Plant 组件 – 供应商 – 工厂
(k, l): Plant-Customer Zone 工厂 – 客户区
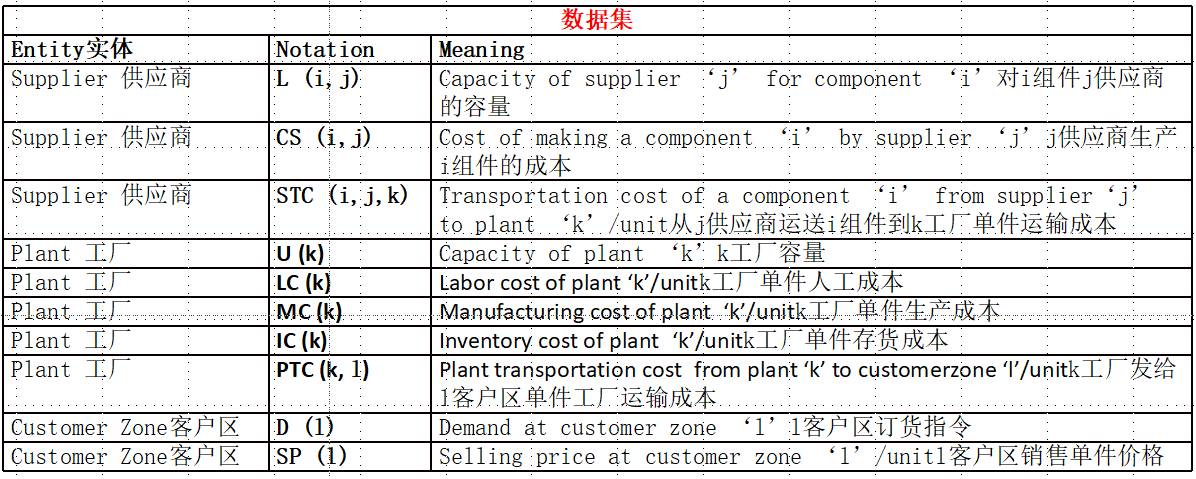
数据集如下

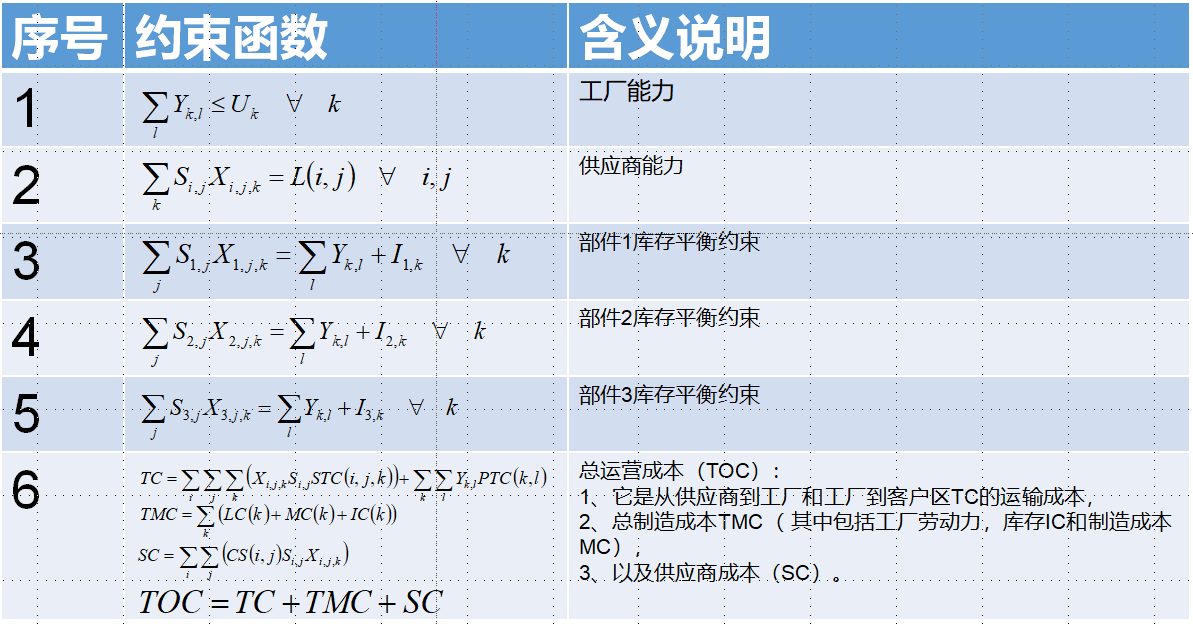
约束函数设计如下

目标函数设计如下

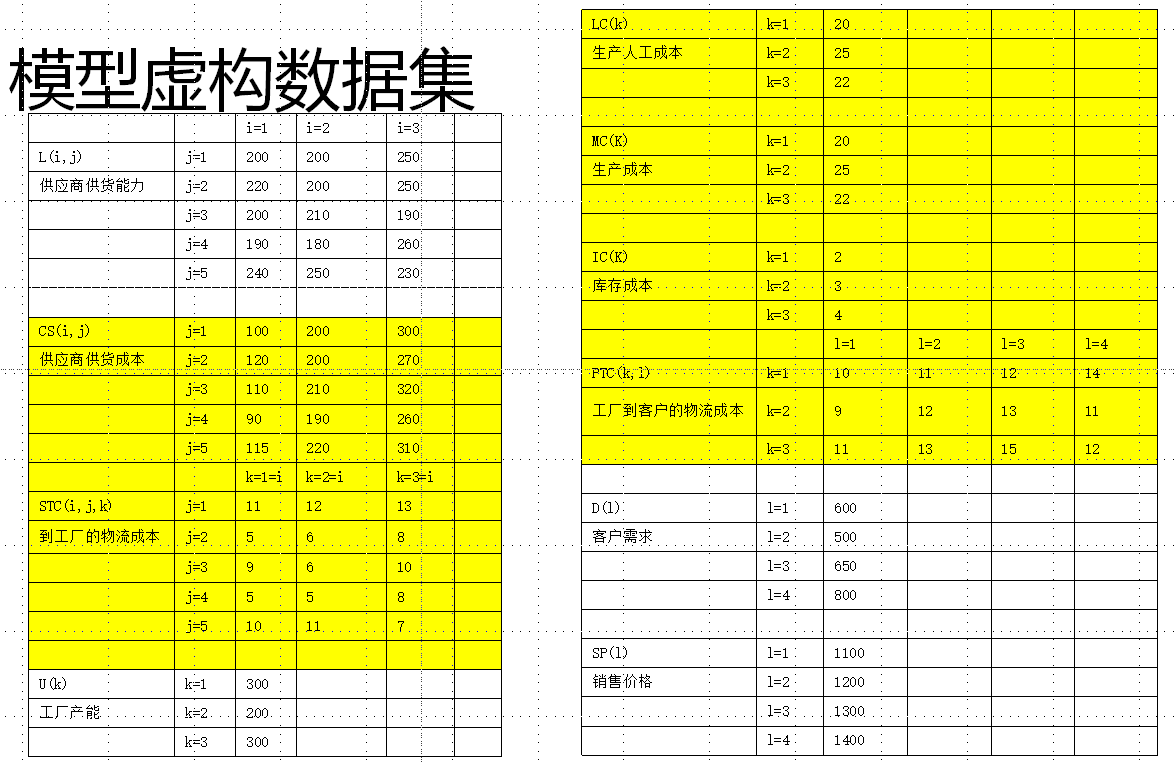
模拟数据集如下

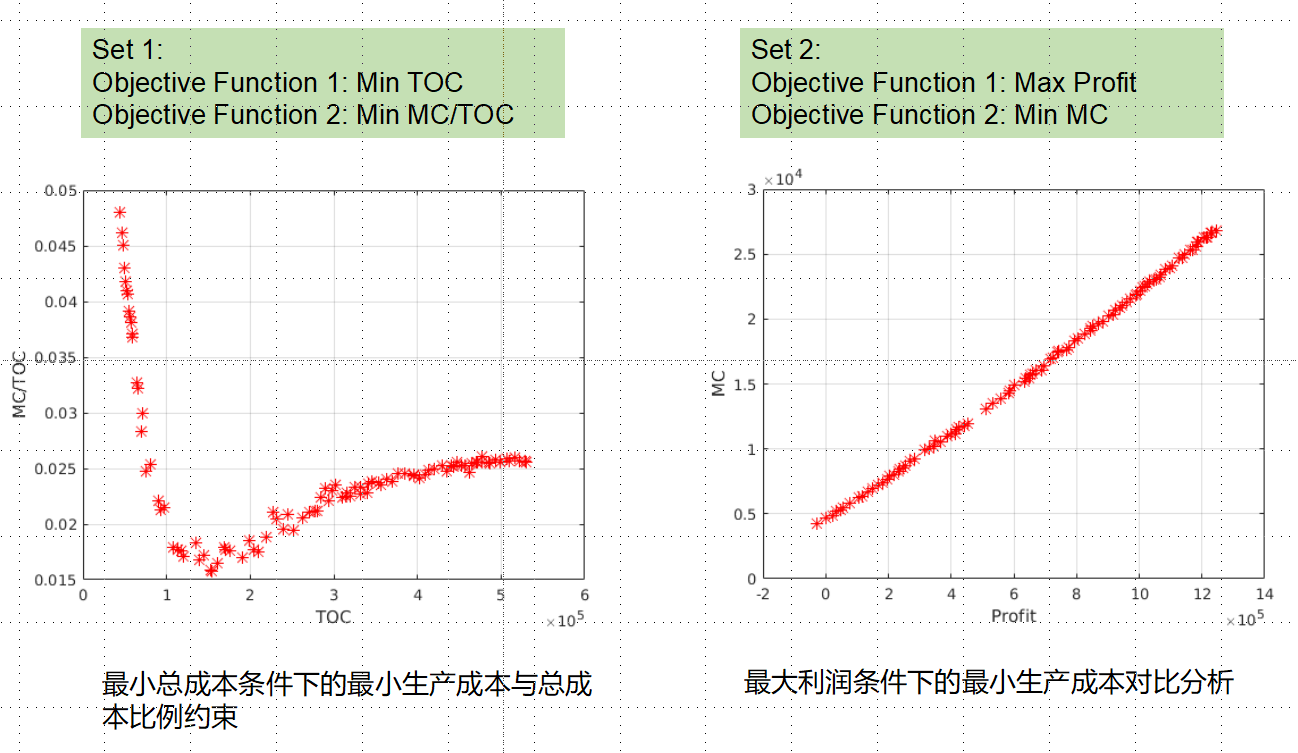
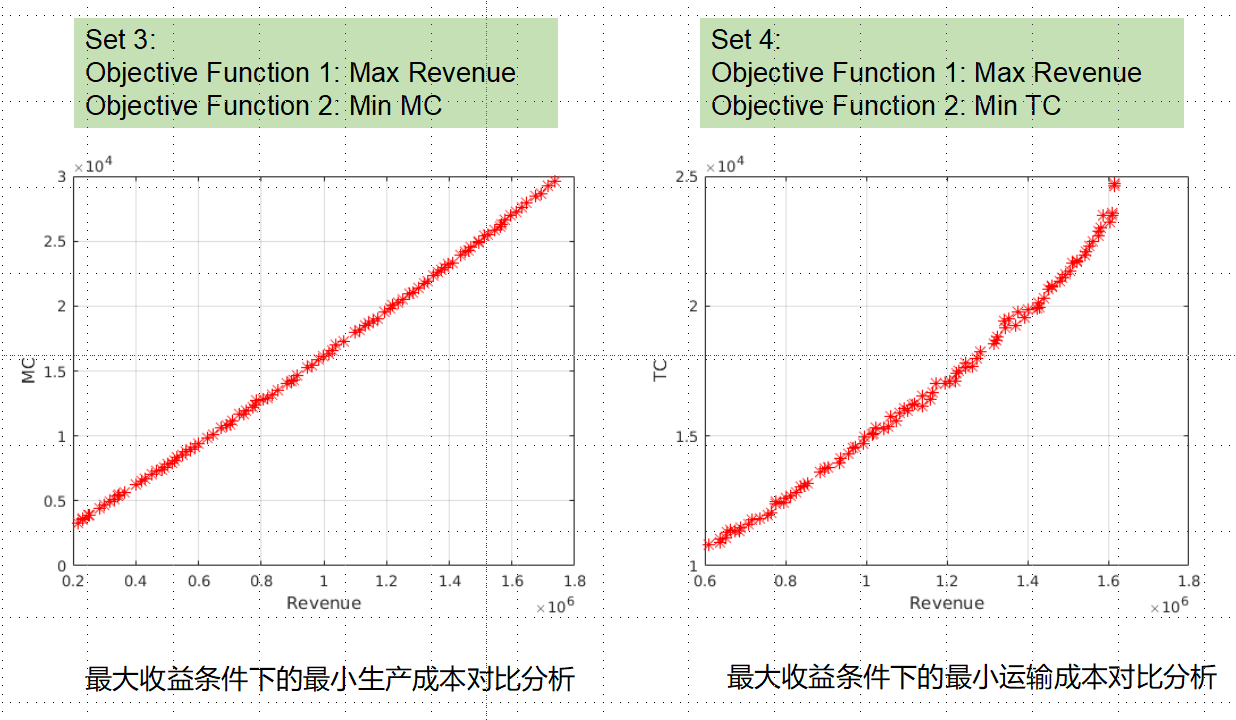
运行结果

今天的文章多目标优化问题的算法及其求解分享到此就结束了，感谢您的阅读。