| ylbtech-学术-几何-维-思维几何:超正方体(几何中的思维方体) |
四维方体
是立方体的四维类比,四维方体之于立方体,就如立方体之于
正方形,四维方体
是四维凸正多胞体,
有8个立方体胞,立方体
维数大于3推广的是超立方体或测度多胞体。
| 1.返回顶部 |
-
中文名:超正方体 外文名:Tesseract 别 称:超立方体或正八面体
-
性 质:四维空间里的几何产物 特 点:无2维距离、角度概念 所属学科:四维几何学
目录
- 1 概述
- 2 投影
- ▪ 施莱格尔
- ▪ 思维方式
- ▪ 球极投影
- 3 展开图
- 4 规律
- 5 符号
- 6 坐标
| 2.返回顶部 |
概述
正八胞体(8-cell,Regular octachoron),
立方体柱(Cubic prism),
4-4边形柱(4-4 duoprism),是
一个四维空间里的几何产物
投影
施莱格尔
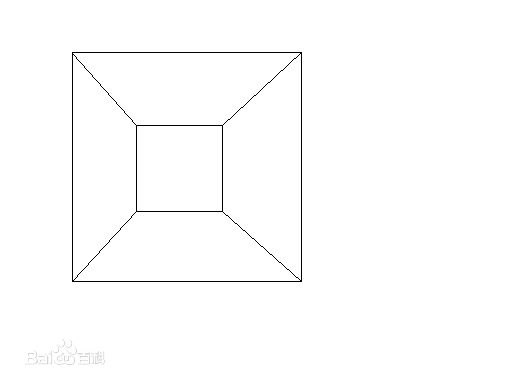
图1
置调整后,可以了解更多。如此获得的图像,不再反映四维方体空间构造,而是反映顶点间的联系。
视网膜上,但四维立方体不能通过普通投影的方式让人们看见,只能先投影成三维的物体,再经过一次投影才能呈现在视网膜上。
三维空间的人类来说,
四维世界是很神秘的概念。正像生活在
二维世界里的小人(如果存在的话)很难想象三维世界一样,我们同样难于想象四维世界。不过也
正像我们可以通过研究三维物体在
二维物体上的投影来研究想象三维物体一样,我们也可以通过
四维物体在三维世界中的
立体图形投影来研究四维世界。
立方体在二维世界中的投影(事实上投影应当是普通的正方形,图为二维生物可能的想象图)。二维小人多多少少可以通过这些投影来想象那个“三 维立方体”的神秘图形。他们可以数出这个
图2
立方体有8个顶点,12条边,6个面。可以看到图1的样子像是一个大正方形套一个小正方形,那我们用一点类比的思维,把一个大立方体“套住”一个小立方体,这就得到一个超正方体的一种
三维投影(当然图2是它的三维投影)
二维世界里(不考虑时间轴)要把不透明图形简化的只有顶点(二维物体中的零维框架)之后二维(如果存在)小人才能看得到内部,在我们在三维世界里要简化到棱长(三维物体中的一维框架)才能看到物体内部。所以二维小人(如果存在)研究三维立方体只会先把三维立方体的顶点投影在二维平面上,在投影成一条一位的直线。
立方体的六个面也要把最外部的正方形也要算进去,超正方体表面的八个立方体也包括“最外部”的那一个
正方形)、32条棱和16个顶点
思维方式
如果四维超正方体不太好想象的话,我们换成球试试吧。三维球嘛,无论从哪个方向投影在
二维平面上都只是一个半径等同的圆形,这样我们就很容易想到
四维球在三维世界中的投影只不过是一个半径等同的球了。如果还想要讨论得深入一些,不妨试试球穿越问题。比如说一个球穿过一个二维平面,二维小人会发现平面上凭空冒出一个慢慢变大的点,后来眼看着扩张成
圆,又慢慢缩小成点,最后突然消失。如果这个令二维小人惊讶不已的事实让你并不觉得奇怪,那么以下的情形你定会吃惊不小;在你面前无中生有地出现一个点,扩成球又缩回点,再突然消失。多么神奇!其 实这只不过是四维球穿越三维世界的情形。
角度概念。
球极投影
Tesseract球极投影
将一个立方体的各个表面膨胀,一段时间后会得到一个球
平行投影。
二维平面上(是直接,不经过三维),但是由于是投影在二维上,会失真得很厉害所以只能够表现一些
点与线之间的连接关系
正投影,ABCD分别是四个轴,注意“相邻”两根轴的
夹角都是45度的。16个
顶点坐标分别是(±1,±1,±1,±1)(下文有简单推导),然后按照给出的一个一个填上去就是的了(方法说上去有点烦,大家可以用几何画板画画这个投影,其实蛮简单的)。
二维线架正投影
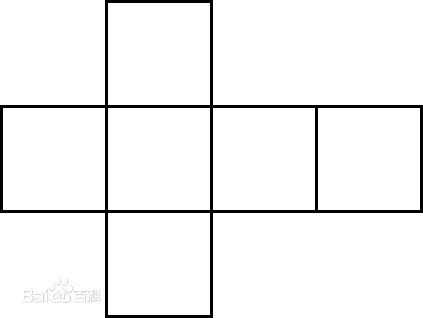
展开图
大家一定知道把
立方体的六个面展开的样子吧,其中一种展开法如右图。
立方体被藏在三维展开图里边了。
二维小人不会明白那六个
正方形怎么转才能拼成一个立方体一样的道理。

规律
立方体(胞),24个面,32条线段,16个点。
符号
施莱夫利符号有几个:

(5张)
坐标
正十六胞体,正十六胞体作类似处理也可以得正八胞体。
| 3.返回顶部 |
1.2

1.3

1.7
1.8

1.9

2.0
2.1
| 4.返回顶部 |
| 5.返回顶部 |
| 6.返回顶部 |
 |
作者:ylbtech 出处:http://ylbtech.cnblogs.com/ 本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。 |
转载于:https://www.cnblogs.com/storebook/p/10691220.html
今天的文章学术-几何-维-四维几何:超正方体(几何中的思维方体)分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/66076.html



