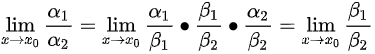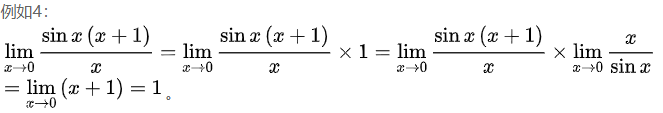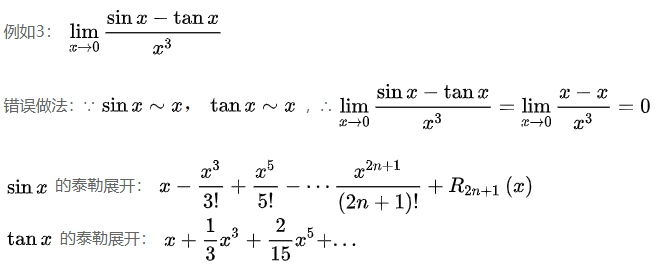主要解决为什么等价无穷小量替换一般只用于乘除，而不用于加减？
有些题目在加减时替换能得到正确答案，有些则不能，它什么时候是可以用于加减的？
目录
一、等价无穷小量的替换的基础知识
1.定义
等价无穷小量的替换：已知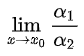
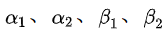
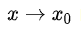
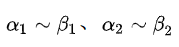
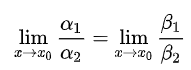
存在，
都是
的无穷小量，且
存在（或为∞），则有
。
证明：
2.用等价无穷小量的注意事项
但用等价无穷小量的替换需要特别注意两点（常出错的两点）
①被替换的量，必须是无穷小量（在取极限时为0）。
②被替换的量，必须是作为被乘或被除的元素，不能是被加减的元素。
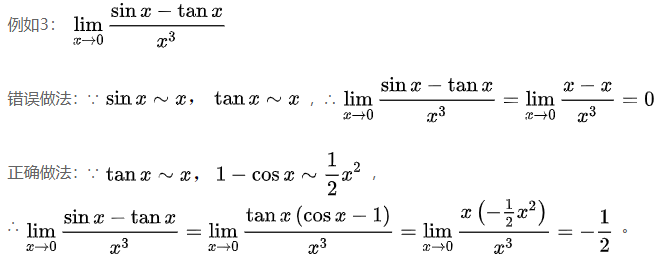
③替换时必须整体替换，而不能替换局部
整体替换是什么意思呢？
其实等价无穷小量的替换，我们可以看做是原极限乘以一个极限为1的分式。
二、深层的去理解等价无穷小量的替换
1.等价无穷小量和泰勒展开式的联系
泰勒展开式：
我们用泰勒展开式，来对函数在一点附近的函数进行近似，近似式的阶数越高，近似程度越好。
都是近似，等价无穷小量和泰勒展开的关系是什么呢？
无穷小量的等价，不过取了泰勒展开式的第一项去等价罢了。
等价无穷小量就是精度较低的泰勒展开。
仅仅从做题的角度来说，就是你能用等价无穷小量去做的题，用泰勒展开一定可以，但反过来未必。
2.为什么加减时我们一般不用等价无穷小量的替换？
我们清楚了等价无穷小量和泰勒展开之间的关系之后，这个问题的答案我们很容易得到。
为什么加减不行？
本质是因为加减可能会导致项的抵消，抵消后，根据分母的阶数可能会需要泰勒展开第一项后的高阶近似，但因为等价无穷小量只取了泰勒展开的第一项，对后续的近似无能为力。
例如上文例3:
就是当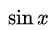
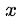
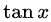
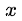
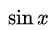
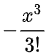
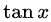
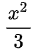
的一阶代表元
（也就是它的等价无穷小量）与
的一阶代表元
（也是它的等价无穷小量）消掉之后，按理说该二阶代表元站出来了（因为分母是三阶的），对于这个例子而言，两者都没有二阶代表元，所以要各自三阶代表元（的
，的
）站出来了，但因为等价无穷小量只取了泰勒展开的第一项，它才不管你的分母是x的几阶无穷小量，消完就没，所以就是0。但我们知道在取完第一项之后后面的项也还是有用（根据分母是x的几阶无穷小量）。
3.为什么乘除时可以无顾忌的用等价无穷小量的替换？
那为什么乘除可以呢？
因为乘除不会消去第一项近似，你等价的那个无穷小量（即泰勒展开的第一项）总会在，在就意味着轮不到你后面的高阶近似上场。
这个时候，我不需要你分子的等价无穷小量一直等价到和分母相同。
举个例子：我把例3的分子化为乘，分母化为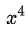 
。
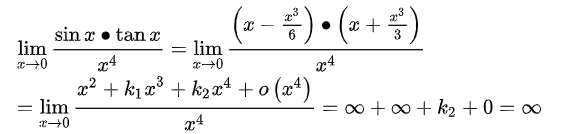
4.什么时候可以在加减中用等价无穷小量的替换?
知道为什么不能用，那什么时候能用就很简单了——我们不让相加减的两个函数的泰勒展开式的第一项（等价的无穷小量）消去就可以了呗。
记录转自知乎：https://zhuanlan.zhihu.com/p/99373470
今天的文章极限等价无穷小替换大全_洛必达法则7种例题分享到此就结束了，感谢您的阅读。
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/67554.html
