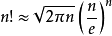不凡的夫夫 斯塔林公式求阶乘位数

https://ac.nowcoder.com/acm/contest/75/A

题意：求解 n! 在八进制下的位数。

一个整数n的位数的计算方法为：log₁₀(n)+1
n=10^m
故n的位数为 m = log10(n!)+1
如12345 = 1.2345*10⁴，那么(int)log10(12345) = 4，再加上1就是这个数的位数。

那么对于 n! 的八进制数的位数长度，log₈n! + 1 即可。

n! 可以通过斯塔林公式来求。

斯塔林公式：

log₈n! = log₈(2 * PI * n)^1/2 + log₈(n/e)ⁿ

          = 1/2 * log₈(2 * PI * n) + n * log₈(n/e)

#include <bits/stdc++.h>
using namespace std;
#define E exp(1)
#define PI acos(-1)
#define log_8(x) log10(x)/log10(8) //通过换底公式来求log8(x)

int main(){ 
   
	int t,n;
	scanf("%d",&t);
	while(t--){ 
   
		scanf("%d",&n);
		int ans = 1;
		if(n > 2){ 
   
			ans = n*log_8(n/E)+log_8(2*PI*n)/2 + 1;		//
		}
		printf("%d\n",ans);
	}

	return 0;
}

今天的文章不凡的夫夫 斯塔林公式求阶乘位数分享到此就结束了，感谢您的阅读。