一个答案不唯一的数独问题是什么_数独题目100道及答案

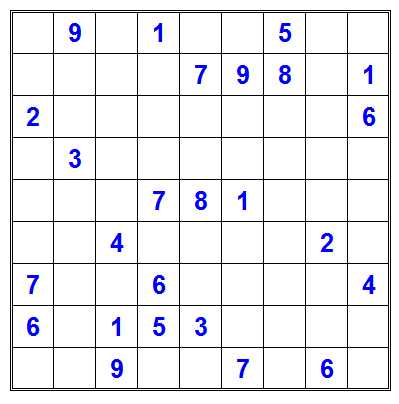
数独问题

这个问题答案不唯一。如何求所有的答案？

论新闻记者的理科修养

有了解数独的代码，就想找一些真的问题来练习。

$n\times n$ 的数独问题，对于非常大的 $n$ 的数独问题目前虽然没有好的计算机或非计算机解法，但是对于 $9\times 9$ 的民间常玩数独还是可以穷举秒解的。

比如，上面的数独问题用 Mathematica 在代码使用正确的情况下，列出所有解，用 i7 K4770 CPU之类的电脑，通常在200秒以内必然能完成。

可能这个问题不够难，于是，尝试搜索最难数独之类的关键词。找到的是一则2013年前后的新闻。说是芬兰某 数学家 用三个月设计出一个号称世界最难的，只有唯一答案的常规数独问题，重庆一位副教授用15天，而江苏一位农民爱好者用3天解出。但是两者的答案不一样。

我验证了下这个问题，记者的专业修养真的是太文科生了。

http://www.sudokufans.org.cn/forums/topic/438/#entry2983

我没有查芬兰某人的身份背景，因为这个并不关键。但是说数独最难必然不是数学家。数学家应该有常识，这类数独问题根本算不上什么问题，更何谈世界最难？难度其实也缺乏一个客观的度量标准。

其次，这类问题的解是不是唯一，用计算机恰当的算法和代码可以10分钟之内必然能穷举出来而验证。那个问题的确是有唯一解的。记者说某网友编程序用24小时，只能说记者的网友代码或算法比较笨而已，并不能说明一般的设计良好的算法求解这类问题的效率。但是这居然也成为一个炒作要点。

从图片看出，重庆的副教授的答案是正确的。这个根本就不意外。记者居然把江苏老农的错误的解答大肆宣扬，还由此否认原始问题解的唯一性，简直是脑残到家。

这不只是专业素质问题，简直是道德品质问题了：为了制造新闻卖点，故意夸大原始问题作者身份及其问题难度，然后拉低江苏老农的身份，并把后者的错误答案当成正确答案来宣传。

一些答案

这里的答案，实际上是算法搜索到的可能的全部答案。
所以，不要尝试人工找其它答案了。

代码:

ColumnQ[l_List]:= And @@MapThread[Unequal,l]
SubMatQ[l_List]:=And @@ (Unequal[Sequence @@ #]& /@ Partition[Flatten[Partition[l,{3,3}]],9])
SubMatPartialQ[l_List,Positions_List]:= SubMatQ @ Join[l,Take[Positions,Length[l]-9]]
genRow[l_List, OneToNine_List]:=
Module[
{nz,cmp,perms},
(* Find the values and locations of the given elements *)
nz = Select[Thread[{l,OneToNine}],#[[1]]>0 &];
(* Find the numbers from 1 to 9 which aren't specified *)
cmp = Complement[OneToNine,nz[[All,1]]];
(* Find the permutations of the numbers not specified *) 
perms = Permutations[cmp];
(* Insert the specified numbers back in *)
Fold[Insert[#1,Sequence @@ #2]&,#,nz]& /@perms
]

TestQ[n_, GivenAndPositions_List]:= (ColumnQ[#]&& SubMatQ[#])& @  ReplacePart[GivenAndPositions, n-> #]&
Function To Build the Solution Using Backtrack 
<<Combinatorica`
BacktrackSolve[GivenValues_List]:=
Module[
{OneToNine = Range[9],Positions,InitialSampleSpace, GivenAndPositions, SampleSpace},
Positions = Outer[Plus, 10*OneToNine,OneToNine];
InitialSampleSpace = genRow[#,OneToNine]& /@ GivenValues;
GivenAndPositions = MapThread[If[#1 ==0,#2,#1]&,{GivenValues,Positions},2];
SampleSpace = Table[Select[InitialSampleSpace[[i]],TestQ[i,GivenAndPositions]],{i,9}];
Backtrack[SampleSpace,(ColumnQ[#] && SubMatPartialQ[#,Positions])&,(ColumnQ[#] && SubMatQ[#])&]
]

myJoin[l1_List, l2_List]:=
If[Length[Dimensions[l1]]==1,Join[{l1},{l2}],Join[l1,{l2}]]
myOuter[l1_List, l2_List,Positions_List]:= Select[Flatten[Outer[myJoin,l1,l2,1],1],(ColumnQ[#] && SubMatPartialQ[#,Positions])&]
OuterSolve[GivenValues_List]:=
Module[
{OneToNine = Range[9],Positions,InitialSampleSpace, GivenAndPositions,SampleSpace},
Positions = Outer[Plus, 10*OneToNine,OneToNine];
InitialSampleSpace = genRow[#,OneToNine]& /@ GivenValues;
GivenAndPositions = MapThread[If[#1 ==0,#2,#1]&,{GivenValues,Positions},2];
SampleSpace = Table[Select[InitialSampleSpace[[i]],TestQ[i,GivenAndPositions]],{i,9}];
Fold[myOuter[#1,#2,Positions]&,First[SampleSpace],Rest[SampleSpace]]
]

AbsoluteTiming[
 MatrixForm /@ 
  OuterSolve[(ToExpression@(Partition[#, 9] &@
       Characters@
        "0810000309000057000000000080000570000000409000501000600080000\ 00016300000400070200"))]]


ConvertString[l_List] := ToExpression[Characters /@ l]
t1str = {"090100500", "000079801", "200005006", "030000700", "000781000", "004000020", "700600004", "601530000", "009007060"};
   MatrixForm[t1 = ConvertString[t1str]]
   AbsoluteTiming[MatrixForm[BacktrackSolve[t1]]]
AbsoluteTiming[MatrixForm /@ OuterSolve[t1]]