深度优先遍历和广度优先遍历对比_深度优先遍历序列怎么写

深度优先遍历和广度优先遍历

什么是 深度/广度 优先遍历？

深度优先遍历简称DFS（Depth First Search），广度优先遍历简称BFS（Breadth First Search），它们是遍历图当中所有顶点的两种方式。

这两种遍历方式有什么不同呢？我们来举个栗子：

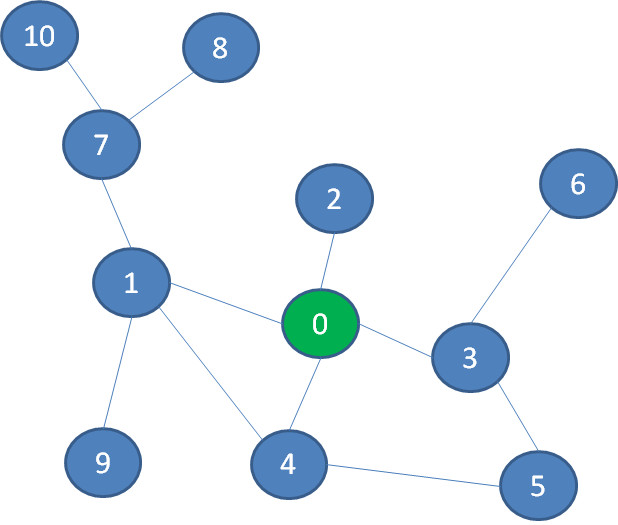
我们来到一个游乐场，游乐场里有11个景点。我们从景点0开始，要玩遍游乐场的所有景点，可以有什么样的游玩次序呢？

第一种是一头扎到底的玩法。我们选择一条支路，尽可能不断地深入，如果遇到死路就往回退，回退过程中如果遇到没探索过的支路，就进入该支路继续深入。

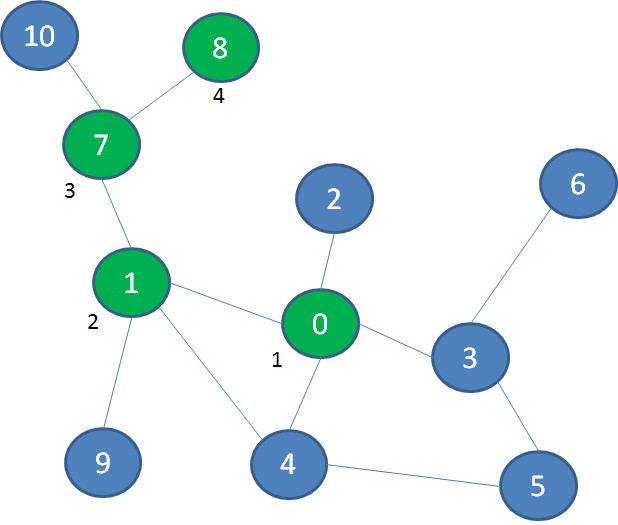
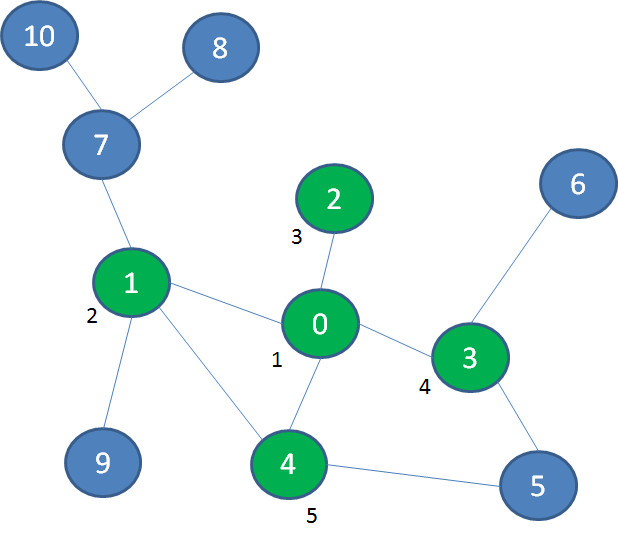
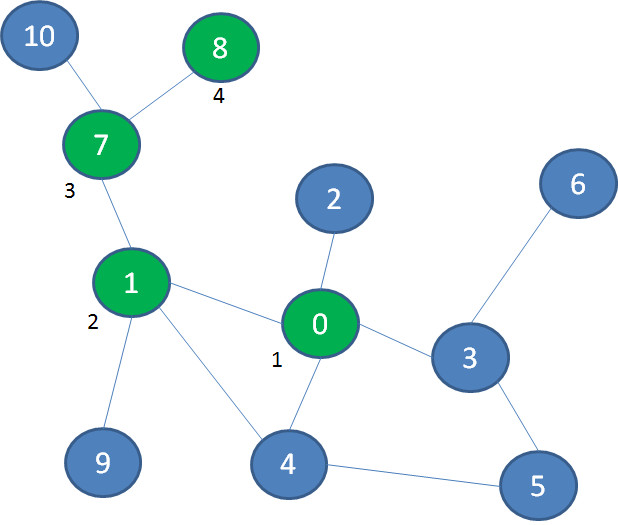
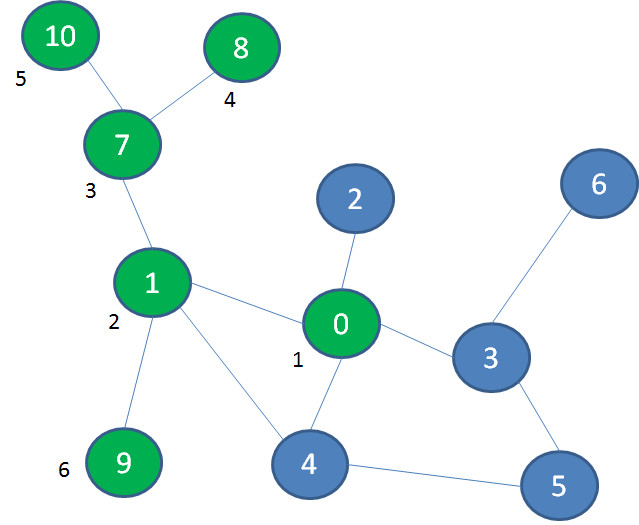
在图中，我们首先选择景点1的这条路，继续深入到景点7、景点8，终于发现走不动了（景点旁边的数字代表探索次序）：

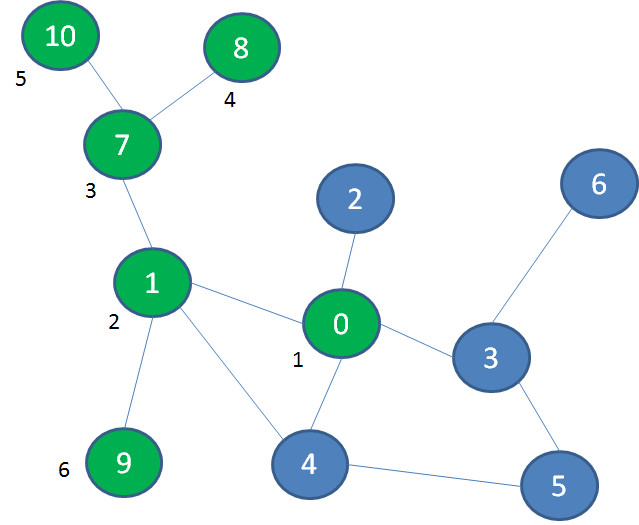
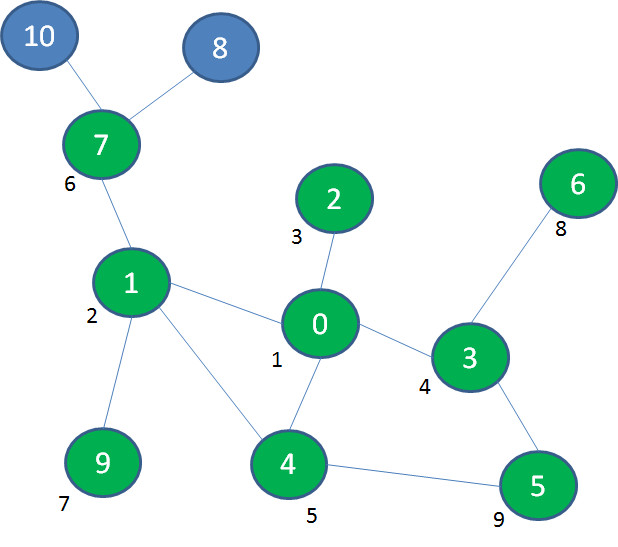
于是，我们退回到景点7，然后探索景点10，又走到了死胡同。于是，退回到景点1，探索景点9：

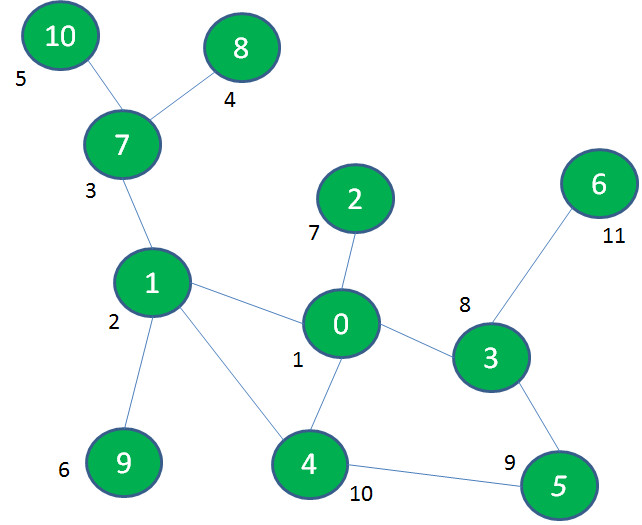
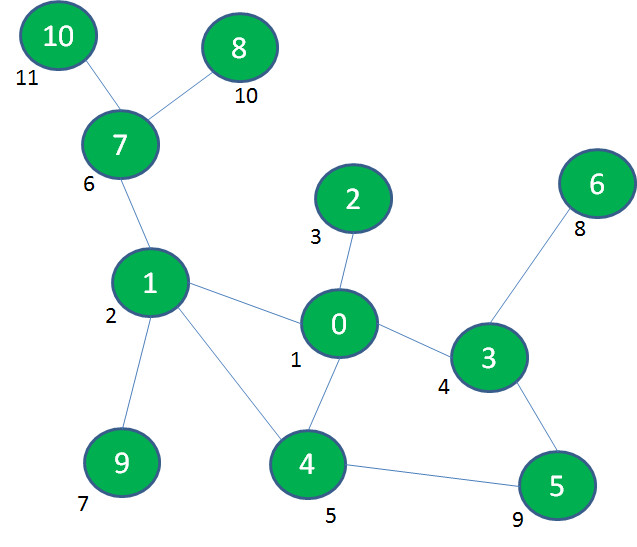
按照这个思路，我们再退回到景点0，后续依次探索景点2、3、5、4、6，终于玩遍了整个游乐场：

像这样先深入探索，走到头再回退寻找其他出路的遍历方式，就叫做深度优先遍历（DFS）。


除了像深度优先遍历这样一头扎到底的玩法以外，我们还有另一种玩法：首先把起点相邻的几个景点玩遍，然后去玩距离起点稍远一些（隔一层）的景点，然后再去玩距离起点更远一些（隔两层）的景点…

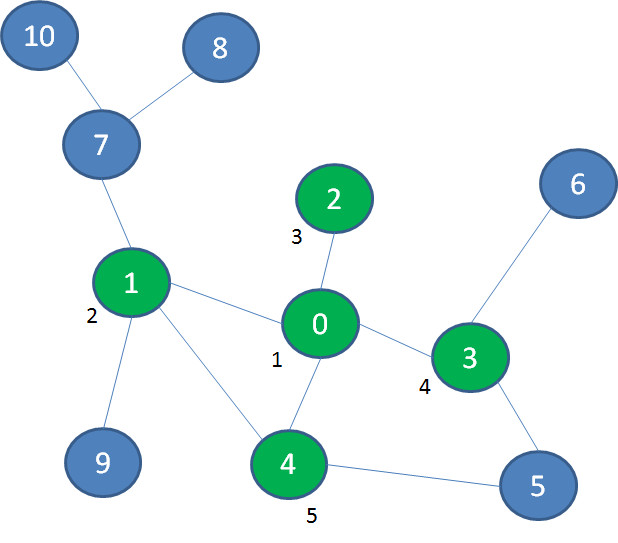
在图中，我们首先探索景点0的相邻景点1、2、3、4：

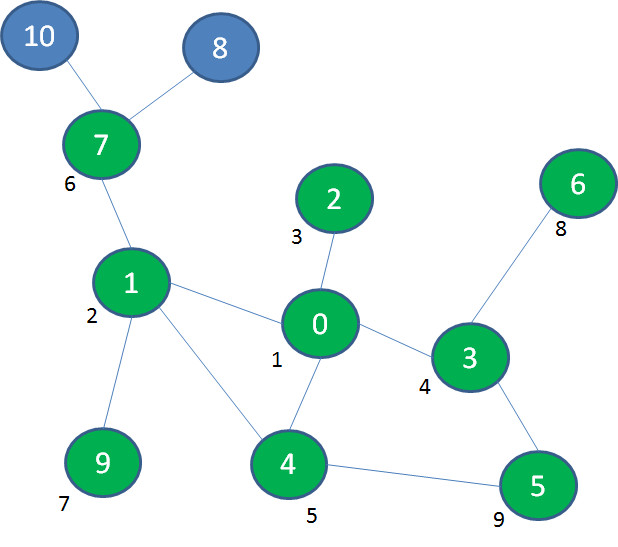
接着，我们探索与景点0相隔一层的景点7、9、5、6：

最后，我们探索与景点0相隔两层的景点8、10：

像这样一层一层由内而外的遍历方式，就叫做广度优先遍历（BFS）。




深度优先遍历

首先说说深度优先遍历的实现过程。这里所说的回溯是什么意思呢？回溯顾名思义，就是自后向前，追溯曾经走过的路径。

我们把刚才游乐场的例子抽象成数据结构的图，假如我们依次访问了顶点0、1、7、8，发现无路可走了，这时候我们要从顶点8退回到顶点7。

![在这里插入图片描述](https://img-blog.csdnimg.cn/20190529211147549.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2EyMjE3MDE4MTAz,size_16,color_FFFFFF,t_70

而后我们探索了顶点10，又无路可走了，这时候我们要从顶点10退回到顶点7，再退回到顶点1。

像这样的自后向前追溯曾经访问过的路径，就叫做回溯。

要想实现回溯，可以利用栈的先入后出特性，也可以采用递归的方式（因为递归本身就是基于方法调用栈来实现）。

下面我们来演示一下具体实现过程。

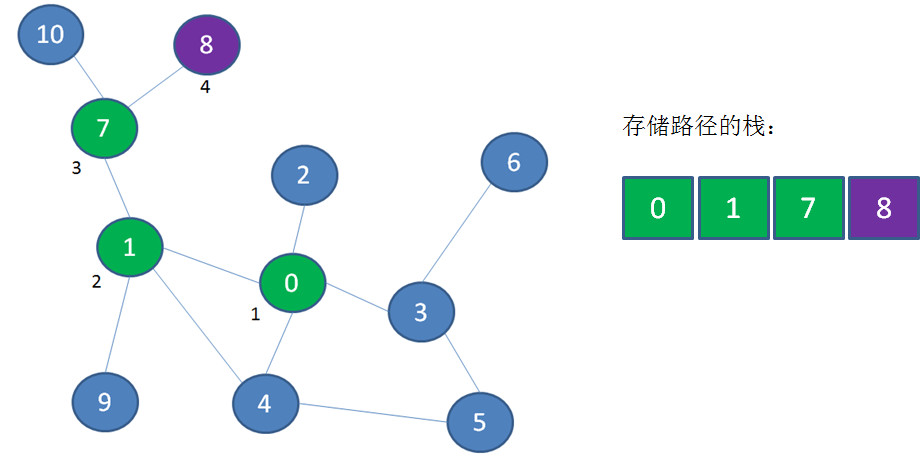
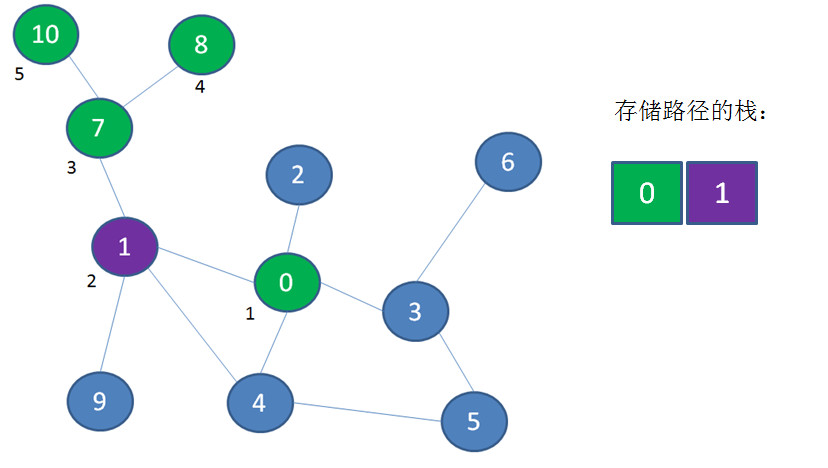
首先访问顶点0、1、7、8，这四个顶点依次入栈，此时顶点8是栈顶：

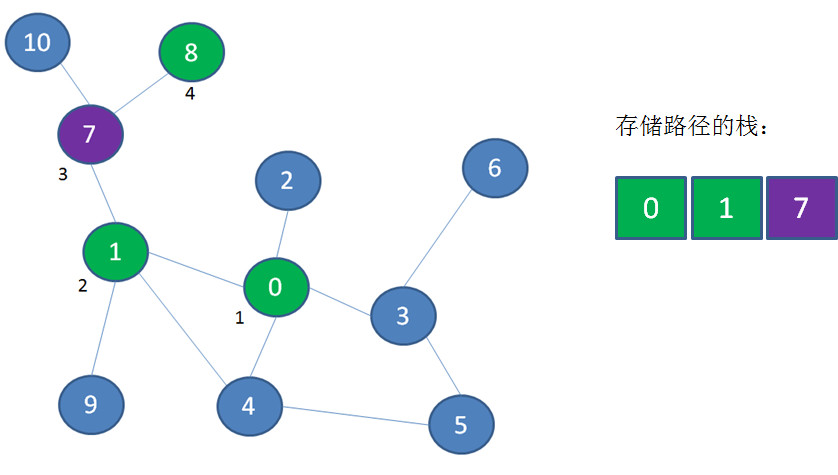
从顶点8退回到顶点7，顶点8出栈：

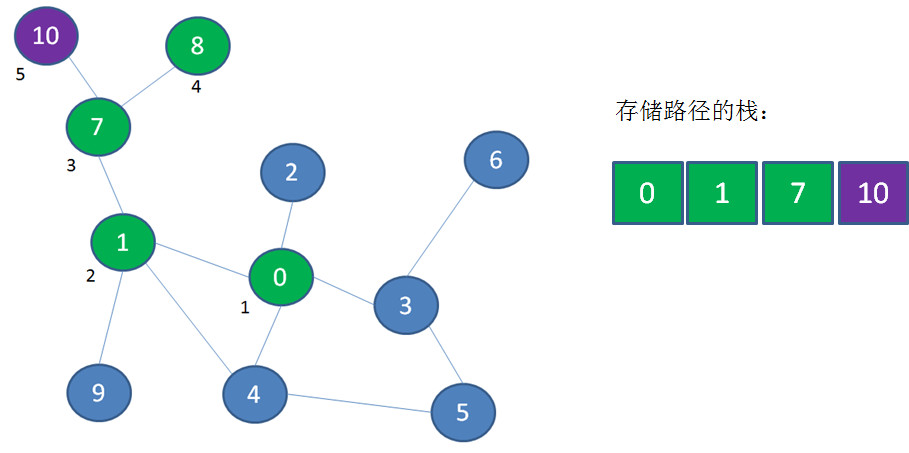
接下来访问顶点10，顶点10入栈：

从顶点10退到顶点7，从顶点7退到顶点1，顶点10和顶点7出栈：

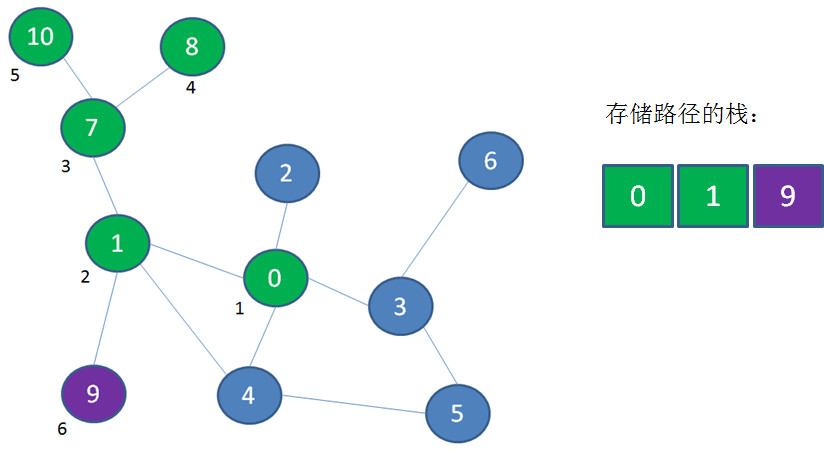
探索顶点9，顶点9入栈：

以此类推，利用这样一个临时栈来实现回溯，最终遍历完所有顶点。

广度优先遍历

接下来该说说广度优先遍历的实现过程了。刚才所说的重放是什么意思呢？似乎听起来和回溯差不多？其实，回溯与重放是完全相反的过程。

仍然以刚才的图为例，按照广度优先遍历的思想，我们首先遍历顶点0，然后遍历了邻近顶点1、2、3、4：

接下来我们要遍历更外围的顶点，可是如何找到这些更外围的顶点呢？我们需要把刚才遍历过的顶点1、2、3、4按顺序重新回顾一遍，从顶点1发现邻近的顶点7、9；从顶点3发现邻近的顶点5、6。

像这样把遍历过的顶点按照之前的遍历顺序重新回顾，就叫做重放。同样的，要实现重放也需要额外的存储空间，可以利用队列的先入先出特性来实现。

下面我们来演示一下具体实现过程。
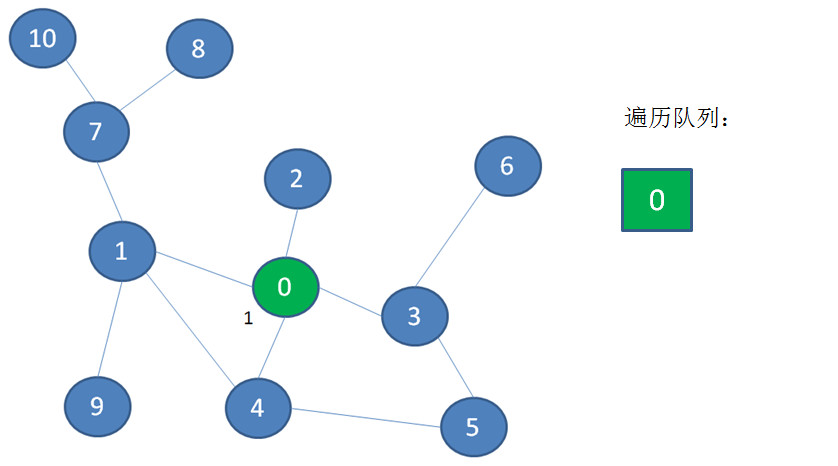
首先遍历起点顶点0，顶点0入队：

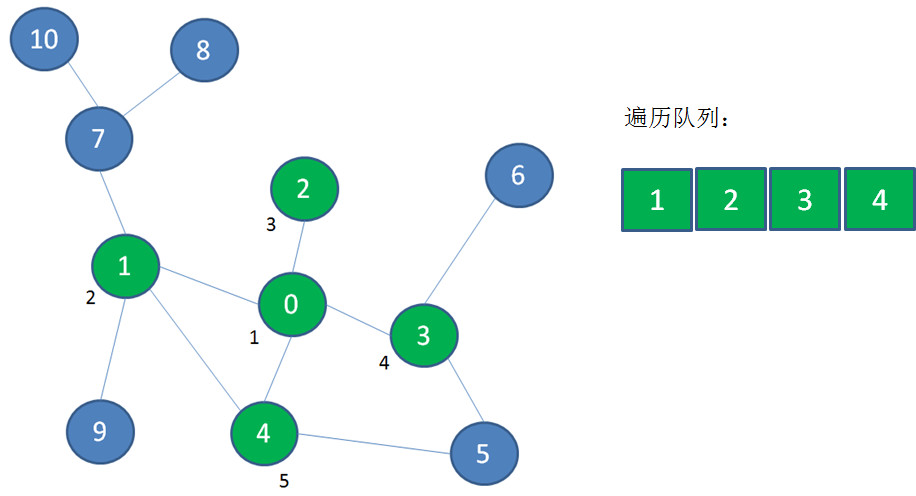
接下来顶点0出队，遍历顶点0的邻近顶点1、2、3、4，并且把它们入队：

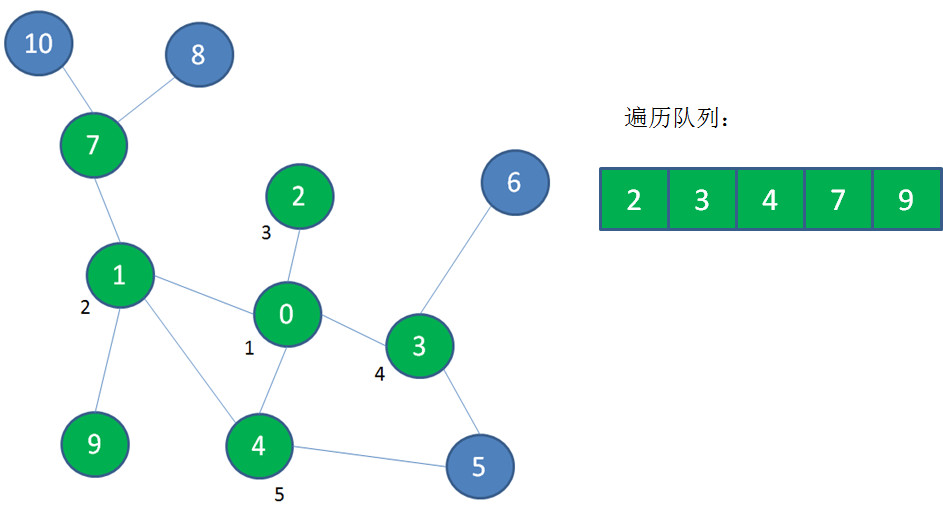
然后顶点1出队，遍历顶点1的邻近顶点7、9，并且把它们入队：

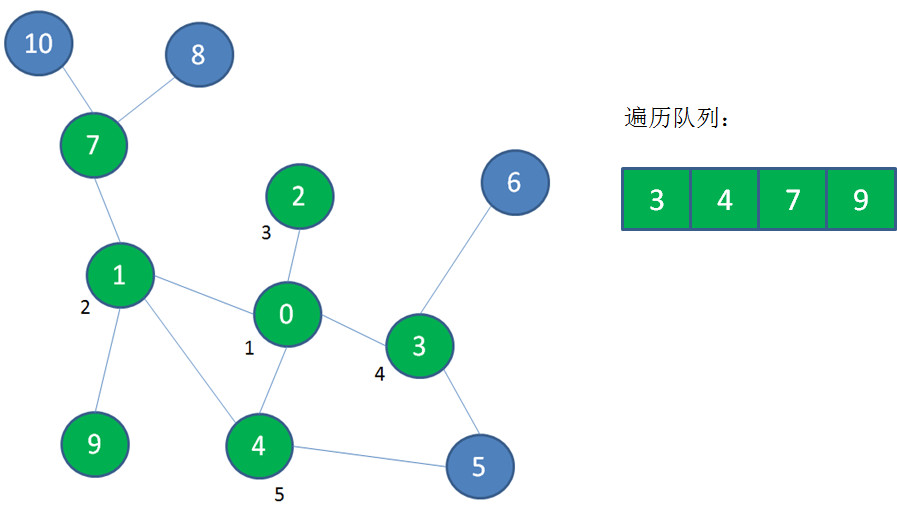
然后顶点2出队，没有新的顶点可入队：

以此类推，利用这样一个队列来实现重放，最终遍历完所有顶点。

/**

图的顶点

/ private static class Vertex { int data; Vertex(int data) {    this.data = data; } } /*

图（邻接表形式）

/ private static class Graph { private int size; private Vertex[] vertexes; private LinkedList adj[]; Graph(int size){    this.size = size;    //初始化顶点和邻接矩阵    vertexes = new Vertex[size];    adj = new LinkedList[size];    for(int i=0; i*

深度优先遍历

/ public static void dfs(Graph graph, int start, boolean[] visited) { System.out.println(graph.vertexes[start].data); visited[start] = true; for(int index : graph.adj[start]){    if(!visited[index]){        dfs(graph, index, visited);    } } } /*

广度优先遍历

*/

public static void bfs(Graph graph, int start, boolean[] visited, LinkedList queue) {

queue.offer(start);

while (!queue.isEmpty()){

   int front = queue.poll();

   if(visited[front]){

       continue;

   }

   System.out.println(graph.vertexes[front].data);

   visited[front] = true;

   for(int index : graph.adj[front]){

       queue.offer(index);;

   }

}

}

public static void main(String[] args) {

Graph graph = new Graph(6);

graph.adj[0].add(1);

graph.adj[0].add(2);

graph.adj[0].add(3);

graph.adj[1].add(0);

graph.adj[1].add(3);

graph.adj[1].add(4);

graph.adj[2].add(0);

graph.adj[3].add(0);

graph.adj[3].add(1);

graph.adj[3].add(4);

graph.adj[3].add(5);

graph.adj[4].add(1);

graph.adj[4].add(3);

graph.adj[4].add(5);

graph.adj[5].add(3);

graph.adj[5].add(4);

System.out.println("图的深度优先遍历：");

dfs(graph, 0, new boolean[graph.size]);

System.out.println("图的广度优先遍历：");

bfs(graph, 0, new boolean[graph.size], new LinkedList());

}

今天的文章深度优先遍历和广度优先遍历对比_深度优先遍历序列怎么写分享到此就结束了，感谢您的阅读。