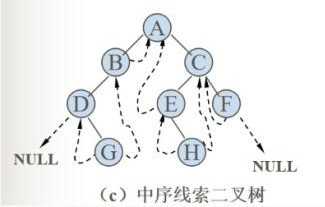
线索二叉树_b树和b+树的区别「建议收藏」

线索二叉树

线索二叉树的概念：

1.线索：
线索是一种对二叉树的操作，意思是对二叉树进行线索化，其目的是使线索化后的二叉树具有方便被遍历的特点，即不使用递归和栈也可以对线索化之后的树进行中序遍历。
2.基于中序遍历的线索二叉树：
中序遍历，即先遍历节点的左孩子，再遍历节点本身，最后遍历节点的右孩子。
3.前驱与后继：
基于这样的顺序得到的对所有节点的遍历顺序中，在某一节点前一个被遍历的节点称之为该节点的前驱，而在该节点后一个被遍历的节点称之为该节点的后继。
4.线索化节点的标记：
线索二叉树的节点定义有所改变，需要两个用来标记其左右孩子是否被线索化的标记变量：可以称为lisThread和risThread,

• 如果lisThread的值为1，则表明该节点的左孩子被线索化，指向该节点的前驱节点；如果lisThread的值为0，则表明该节点的左孩子没有被线索化，指向其左孩子本身。
• 如果risThread的值为1，则表明该节点的右孩子被线索化，指向该节点的后继节点；如果risThread的值为0，则表明该节点的右孩子没有被线索化，指向其右孩子本身。

线索化算法的思路及意义

线索化算法： 我们使用以下算法对一颗二叉树进行线索化，在对一颗二叉树进行中序遍历的过程中，
如果某一节点的左孩子为空，那么将其左孩子指向该节点的前驱，
如果某一节点的右孩子为空，那么再将其右孩子指向该节点的后继。

线索化二叉树的算法描述起来很简单，但是为什么要这样对树进行线索化，其目的和意义是什么，我们下面进行分析：
首先我们要明确线索二叉树存在的意义，即就是可以在不使用递归和栈的情况下更快地对树进行遍历，这样可以提高算法的效率，也就是说，我们将会使用线索来代替递归的功能，在原本不得不用递归来获得某一结点后继节点的情况下，我们使用线索的功能来解除这样的限制。
那我接下来我们需要分析，在哪些情况下一个节点的后继需要通过递归调用的结束来得到？
首先排除一种可能，如果一个节点有右儿子，那么肯定不需要在递归结束返回时获得它的后继，因为根据中序遍历的顺序，它的后继一定是其右分支上的某一个节点，这完全可以通过不断访问其右分支然后判断每一个节点是否有左儿子来得到。
而如果一个节点没有右儿子，那么说明它的后继不在它的右分支上，我们如果不通过递归和栈的性质将无法获得其后继，这时候我们就可以通过建立线索来确定它的后继节点。
显然当该节点没有右儿子时，我们使用一般的顺序遍历无法获得其后继时，我们就希望将它的空的右儿子加以利用，使其直接指向它的后继节点，这样当我们在进行顺序遍历时，就可以通过该线索直接找到它的后继而避免了使用栈和递归的开销。
那么问题来了，似乎我们只需要有右孩子的线索化就可以完成对树的非递归非栈遍历了，所以左孩子的线索化有什么意义？
关于这个问题，书上似乎没有明确指出，我自己的理解是

• 首先左孩子的一个用处就是，给定线索化二叉树中的一个节点，我们只要不断地访问它的左孩子，就一定可以得到中序遍历的第一个节点
• 基于对称的关系，我们不但可以通过不断访问左孩子来得到中序遍历的第一个节点，同样也可以通过访问右孩子来得到中序遍历的最后一个节点，然后我们将遍历的顺序和规则对称变换，就可以通过左孩子的线索化来得到中序遍历的逆序顺序。

线索化二叉树的代码实现

#include <stdio.h>
#include <stdlib.h>
typedef struct TreeNode
{ 
   
	char data;
	struct TreeNode * left;
	struct TreeNode * right;
	int LisThread;
	int RisThread; 
}*BiTree;
BiTree pre=NULL;//声明全局变量，表示在中序遍历过程中当前节点的前驱 
void CreatTree(BiTree *t)
{ 
   
	char data;
	scanf("%c",&data);
	getchar();
	if(data=='0')
	{ 
   
		*t=NULL;
		return;
	}
	else 
	{ 
   
	*t=malloc(sizeof(struct TreeNode));
	(*t)->data=data;
	printf("请输入左节点：\n");
	CreatTree(&(*t)->left);
	printf("请输入右节点：\n");
	CreatTree(&(*t)->right);
    }
}

void InThreading(BiTree t)//对二叉树进行中序线索化 
{ 
   
    if(t==NULL)  return;
    InThreading(t->left);//对左孩子进行线索化 
    
	if(t->left==NULL)
	{ 
   
		t->LisThread=1;
		t->left=pre;
	 } 
	if(pre!=NULL&&pre->right==NULL)
	{ 
   
		pre->RisThread=1;
		pre->right=t;
	}
	pre=t;
	
	InThreading(t->right);	//对右孩子进行线索化 
}

void InOrderThreading(BiTree t)//中序遍历线索化二叉树 
{ 
   
	while(t!=NULL)
	{ 
   
		while(!t->LisThread)
		{ 
   
			t=t->left;
		}
		printf("%c ",t->data);
		while(t->RisThread)
		{ 
   
			t=t->right;
			printf("%c ",t->data);
		}
	    t=t->right;
	}
}
main()
{ 
   
 BiTree t=NULL;
 CreatTree(&t);
 InThreading(t);
 InOrderThreading(t);
}

今天的文章线索二叉树_b树和b+树的区别「建议收藏」分享到此就结束了，感谢您的阅读。