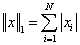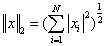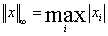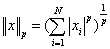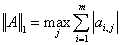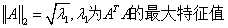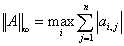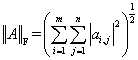矩阵的模和范数_范数和模的区别「建议收藏」

矩阵范数（matrix norm）是数学中矩阵论、线性代数、泛函分析等领域中常见的基本概念，是将一定的矩阵空间建立为赋范向量空间时为矩阵装备的范数。应用中常将有限维赋范向量空间之间的映射以矩阵的形式表现，这时映射空间上装备的范数也可以通过矩阵范数的形式表达。
矩阵范数却不存在公认唯一的度量方式, 一般来讲矩阵范数除了正定性，齐次性和三角不等式之外，还规定其必须满足相容性：。所以矩阵范数通常也称为相容范数。

如果║·║α是相容范数，且任何满足║·║β≤║·║α的范数║·║β都不是相容范数，那么║·║α称为极小范数。对于n阶实方阵（或复方阵）全体上的任何一个范数║·║，总存在唯一的实数k>0，使得k║·║是极小范数。
注：如果不考虑相容性，那么矩阵范数和向量范数就没有区别，因为mxn矩阵全体和mn维向量空间同构。引入相容性主要是为了保持矩阵作为线性算子的特征，这一点和算子范数的相容性一致，并且可以得到Mincowski定理以外的信息。

首先给出向量范数及矩阵范数的计算方法（来自JIMYE的博客）：

1、向量范数

1-范数：，即向量元素绝对值之和，matlab调用函数norm(x, 1) 。

2-范数：，Euclid范数（欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开方，matlab调用函数norm(x, 2)。

∞-范数：，即所有向量元素绝对值中的最大值，matlab调用函数norm(x, inf)。

-∞-范数：，即所有向量元素绝对值中的最小值，matlab调用函数norm(x, -inf)。

p-范数：，即向量元素绝对值的p次方和的1/p次幂，matlab调用函数norm(x, p)。

2、矩阵范数

1-范数：，列和范数，即所有矩阵列向量绝对值之和的最大值，matlab调用函数norm(A, 1)。

2-范数：，谱范数，即A’A矩阵的最大特征值的开平方。matlab调用函数norm(x, 2)。

∞-范数：，行和范数，即所有矩阵行向量绝对值之和的最大值，matlab调用函数norm(A, inf)。

F-范数：，Frobenius范数，即矩阵元素绝对值的平方和再开平方，matlab调用函数norm(A, ’fro‘)。

另外，对于范数的其他性质，有如下定义：

诱导的范数

把矩阵看作线性算子，那么可以由向量范数诱导出矩阵范数

║A║ = max{║Ax║：║x║=1}= max{║Ax║/║x║： x≠0}

它自动满足对向量范数的相容性

║Ax║ ≤ ║A║║x║

并且可以由此证明：

║AB║ ≤ ║A║║B║。

注：

⒈ 上述定义中可以用max代替sup是因为有限维空间的单位闭球是紧的（有限开覆盖定理），从而上面的连续函数可以取到最值。

⒉ 单位矩阵的算子范数为1。

常用的三种p-范数推导出的矩阵范数：

1-范数：

║A║1 = max{ ∑|ai1|，∑|ai2|，……，∑|ain| } （列和范数，A每一列元素绝对值之和的最大值）（其中∑|ai1|第一列元素绝对值的和∑|ai1|=|a11|+|a21|+…+|an1|，其余类似）；

2-范数：

║A║2 = A的最大奇异值 = (max{ λi(AH*A) }) 1/2 （谱范数，即A^H*A
特征值λi中最大者λ1的平方根，其中AH为A的转置
共轭矩阵）；

∞-范数：

║A║∞ = max{ ∑|a1j|，∑|a2j|,…，∑|amj| } （行和范数，A每一行元素绝对值之和的最大值）（其中∑|a1j| 为第一行元素绝对值的和，其余类似）；

其它的p-范数则没有很简单的表达式。

对于p-范数而言，可以证明║A║p=║AH║q，其中p和q是共轭指标。

简单的情形可以直接验证：║A║1=║AH║∞，║A║2=║AH║2，一般情形则需要利用║A║p=max{yH*A*x：║x║p=║y║q=1}。

非诱导范数

有些矩阵范数不可以由向量范数来诱导，比如常用的Frobenius范数（也叫Euclid范数，简称F-范数或者E-范数）：

║A║F= （∑∑ aij2）1/2 (A全部元素平方和的平方根）。

容易验证F-范数是相容的，但当min{m,n}>1时F-范数不能由向量范数诱导（||E11+E22||F=2>1）。

可以证明任一种矩阵范数总有与之相容的向量范数。

例：

定义║x║=║X║，其中X=[x,x，…，x]是由x作为列的矩阵。由于向量的F-范数就是2-范数，所以F-范数和向量的2-范数相容。

另外还有以下结论：

║AB║F <= ║A║F ║B║2

║AB║F ≤ ║A║2 ║B║F

矩阵谱半径

定义：

A是n阶方阵，λi是其特征值，i=1,2，…，n。则称特征值的绝对值的最大值为A的谱半径，记为ρ（A）。

注：注意要将谱半径与谱范数（2-范数）区别开来，谱范数是指A的最大奇异值，即AH*A最大特征值的算术平方根。

谱半径是矩阵的函数，但不是矩阵范数。谱半径和范数的关系是以下几个结论：

定理1：

谱半径不大于矩阵范数，即ρ(A)≤║A║。

因为任一特征对λ，x,Ax=λx，可得Ax=λx。两边取范数并利用相容性即得结果。

定理2：

对于任何方阵A以及任意正数e，存在一种矩阵范数使得║A║<ρ（A)+e。

定理3(Gelfand定理）：

ρ（A)=lim_{k->；∞} ║Ak║1/k。

推论：

推论1：矩阵序列 I,A,A2，…Ak，… 收敛于零的充要条件是ρ（A)<1。

推论2：级数 I+A+A2+… 收敛到（I-A)-1的充要条件是ρ（A)<1。

酉不变范数

定义：

如果范数║·║满足║A║=║UAV║对任何矩阵A以及酉矩阵U,V成立，那么这个范数称为酉不变范数。

容易验证，2-范数和F-范数是酉不变范数。因为酉变换不改变矩阵的奇异值，所以由奇异值得到的范数是酉不变的，比如2-范数是最大奇异值，F-范数是所有奇异值组成的向量的2-范数。反之可证明，所有的酉不变范数都和奇异值有密切联系：

Von Neumann定理：在酉不变范数和对称度规函数（symmetric gauge function）之间存在一一对应关系。也就是说任何酉不变范数事实上就是所有奇异值的一个对称度规函数。

今天的文章矩阵的模和范数_范数和模的区别「建议收藏」分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/71894.html