摘要：本文详细介绍Kmeans聚类算法的原理和程序实现。首先介绍利用该算法的原理及理解，详细介绍基于MATLAB设计一个自定义的Kmeans函数过程，然后利用该函数对UCI的数据集进行聚类以测试聚类结果。代码见文末介绍，后续章节将介绍的主要部分有：

1. 前言

作为无监督聚类算法中的代表——K均值聚类（Kmeans）算法，该算法的主要作用是将相似的样本自动归到一个类别中。所谓的监督算法，就是输入样本没有对应的输出或标签。聚类（clustering）试图将数据集中的样本划分为若干个通常是不相交的子集，每个子集称为一个“簇（cluster）”，聚类既能作为一个单独过程，用于找寻数据内在的分布结构，也可作为分类等其他学习任务的前去过程。——《Machine Learning》

聚类算法也许是机器学习中“新算法”出现最多、最快的领域，一个重要的原因是聚类不存在客观标准，给定数据集总能从某个角度找到以往算法未覆盖的某种标准从而设计出新算法。Kmeans算法十分简单易懂而且非常有效，但是合理的确定K值和K个初始类簇中心点对于聚类效果的好坏有很大的影响。众多的论文基于此都提出了各自行之有效的解决方案，新的改进算法仍然不断被提出，此类文章大家可以在Web Of Science中搜索。

尽管Kmeans算法在MATLAB、Python等语言的工具箱函数中都有自带的函数可供调用，但作为机器学习的研究者新来说要设计出新的算法，有时就得“定制”自己的Kmeans函数了。自己动手编写无疑也更加能理解算法的具体过程，接下来就让我们进入正题吧

2. Kmeans算法的原理与理解

Kmeans算法是最常用的聚类算法，主要思想是:在给定K值和K个初始类簇中心点的情况下，把每个点(亦即数据记录)分到离其最近的类簇中心点所代表的类簇中，所有点分配完毕之后，根据一个类簇内的所有点重新计算该类簇的中心点(取平均值)，然后再迭代的进行分配点和更新类簇中心点的步骤，直至类簇中心点的变化很小，或者达到指定的迭代次数。

2.1 基本原理

假定给定数据样本X，包含了n个对象 X = { X 1 , X 2 , X 3 , . . . , X n } X=\left \{ X_{1} ,X_{2},X_{3},…,X_{n}\right \} X={
X1​,X2​,X3​,…,Xn​},其中每个对象都具有m个维度的属性。Kmeans算法的目标是将n个对象依据对象间的相似性聚集到指定的k个类簇中，每个对象属于且仅属于一个其到类簇中心距离最小的类簇中。对于Kmeans，首先需要初始化k个聚类中心 { C 1 , C 2 , C 3 , . . . , C k } , 1 < k ≤ n \left \{ C_{1} ,C_{2},C_{3},…,C_{k}\right \},1<k\leq n {
C1​,C2​,C3​,…,Ck​},1<k≤n,然后通过计算每一个对象到每一个聚类中心的欧式距离，如下式所示$$dis(X_i,C_j)=\sqrt{\sum _{t=1}^m(X_{it}-C_{jt}{)}^2}$$
上式中，$X_i$表示第i个对象$1\le i\le n$,$C_j$表示第j个聚类中心的$1\le j\le k$，$X_{it}$表示第i个对象的第t个属性，$1\le t\le m$，$C_{jt}$表示第j个聚类中心的第t个属性。

依次比较每一个对象到每一个聚类中心的距离，将对象分配到距离最近的聚类中心的类簇中，得到k个类簇 { S 1 , S 2 , S 3 , . . . , S k } \left \{ S_{1},S_{2},S_{3},…,S_{k} \right \} {
S1​,S2​,S3​,…,Sk​}

Kmeans算法用中心定义了类簇的原型，类簇中心就是类簇内所有对象在各个维度的均值，其计算公式如下$$C_t=\frac{{\sum }_{X_i\in S_l}{X}_i}{\left|S_l\right|}$$
式中，$C_l$表示第l个聚类的中心，$1\le l\le k$，$\left|S_l\right|$表示第l个类簇中对象的个数，$X_i$表示第l个类簇中第i个对象，$1\le i\le \left|S_l\right|$。

2.2 算法流程

输入：样本集 D = { x 1 , x 2 , x 3 , . . . , x m } D=\left \{ x_{1},x_{2},x_{3},…,x_{m} \right \} D={
x1​,x2​,x3​,…,xm​}；聚类簇数k.
过程：
1：从D中随机选择k个样本作为初始均值向量 { μ 1 , μ 2 , μ 3 , . . . , μ k } \left \{ \mu _{1},\mu _{2},\mu _{3},…,\mu _{k} \right \} {
μ1​,μ2​,μ3​,…,μk​}
2：repeat
3： 令$C_i=\varnothing (1⩽i⩽k)$
4： for j=1,2,…,m do
5： 计算样本$x_j$与各均值向量${\mu }_i(1⩽i⩽k)$的距离：$d_{ji}={\Vert x_j-{\mu }_i\Vert }_2$;
6： 根据距离最近的均值向量确定$x_j$的簇标记： λ j = a r g m i n i ∈ { 1 , 2 , 3 , . . . , k } d j i \lambda _{j}=arg min_{i\in \left \{ 1,2,3,…,k \right \}}d_{ji} λj​=argmini∈{
1,2,3,…,k}​dji​；
7： 将样本$x_j$划入相应的簇： C λ j = C λ j ∪ { x j } ； C_{\lambda_{j}}=C_{\lambda_{j}}\cup \left \{ x_{j} \right \}； Cλj​​=Cλj​​∪{
xj​}；
8： end for
9： for i=1,2,…,k do
10: 计算新均值向量：${\mu }_i^{{}^{\prime }}=\frac{1}{|C_i|}{\sum }_{x\in C_i}x$;
11： if ${\mu }_i^{{}^{\prime }}\ne {\mu }_i$ then
12： 将当前均值向量 ${\mu }_i$更新为${\mu }_i^{{}^{\prime }}$
13： else
14： 保持当前均值不变
15： end if
16： end for
17：until 当前均值向量均未更新
输出：簇划分 C = { C 1 , C 2 , . . . , C k } C=\left \{ C_{1} ,C_{2},…,C_{k} \right \} C={
C1​,C2​,…,Ck​}

以上算法流程引自周志华《机器学习》，从流程来看K-means算法计算步骤基本上可以概括为两个部分：（1）计算每一个对象到类簇中心的距离；（2）根据类簇内的对象计算新的簇类中心。

3. 编程实现

为了方便应用我们将其编写为一个M函数KMeans()，首先需要确定函数的输入输出。这里输入参数为：data，K，iniCentriods，iterations（其中data为输入的不带标号的数据集数据矩阵，大小为numOfDatanumOfAttributes，K为数据分的类簇数目，iniCentriods为自行指定的初始聚类中心矩阵，大小为KnumOfAttributes，iterations为算法迭代次数。）
输出参数为：Idx，centroids，Distance（Idx为返回的分类标号， centroids为每一类的中心，Distance为类内总距离）

根据前面2.2节中的算法流程编写Kmeans算法的MATLAB程序如下

%% Kmeans算法
% 输入：
% data 输入的不带分类标号的数据
% K 数据一共分多少类
% iniCentriods 自行指定初始聚类中心
% iterations 迭代次数

% 输出：
% Idx 返回的分类标号
% centroids 每一类的中心
% Distance 类内总距离

 
function [Idx,centroids,Distance]=KMeans(data,K,iniCentriods,iterations)
[numOfData,numOfAttr]=size(data); % numOfData是数据个数，numOfAttr是数据维数
centroids=iniCentriods;
%% 迭代
for iter=1:iterations
    pre_centroids=centroids;% 上一次求得的中心位置
    
    tags=zeros(numOfData,K);
    %% 寻找最近中心，更新中心
    for i=1:numOfData
        D=zeros(1,K);% 每个数据点与每个聚类中心的标准差
        Dist=D;
        
        % 计算每个点到每个中心点的标准差
        for j=1:K
            Dist(j)=norm(data(i,:)-centroids(j,:),2);
        end
        
        [minDistance,index]=min(Dist);% 寻找距离最小的类别索引
        tags(i,index)=1;% 标记最小距离所处的位置（类别）
    end
    
    
    %% 取均值更新聚类中心点
    for i=1:K
        if sum(tags(:,i))~=0
            % 未出现空类，计算均值作为下一聚类中心
            for j=1:numOfAttr
                centroids(i,j)=sum(tags(:,i).*data(:,j))/sum(tags(:,i));
            end
        else % 如果出现空类，从数据集中随机选中一个点作为中心
            randidx = randperm(size(data, 1));
            centroids(i,:) = data(randidx(1),:);
            tags(randidx,:)=0;
            tags(randidx,i)=1;
        end
    end
    
   
    if sum(norm(pre_centroids-centroids,2))<0.001  % 不断迭代直到位置不再变化
        break;
    end
    
    
end

%% 计算输出结果
Distance=zeros(numOfData,1);
Idx=zeros(numOfData,1);
for i=1:numOfData
    D=zeros(1,K);% 每个数据点与每个聚类中心的标准差
    Dist=D;
    % 计算每个点到每个中心点的标准差
    for j=1:K
        Dist(j)=norm(data(i,:)-centroids(j,:),2);
    end
    
    [distance,idx]=min(Dist);% 寻找距离最小的类别索引
    distance=Dist(idx);
    
    Distance(i)=distance;
    Idx(i)=idx;
end
Distance=sum(Distance,1);% 计算类内总距离
end

在以上代码中其最主要部分在于第18至58行，进行寻找最近中心和求取均值更新聚类中心点。值得注意的是，在聚类过程中可能会出现空类即代码第44行那样，为保证算法的继续运行，从数据集中随机选取一个点作为中心。

4. 聚类结果评价

为了验证编写的Kmeans函数的性能，这里对想用的UCI数据集Iris数据集进行聚类并计算聚类的准确率，Iris数据集可以在http://archive.ics.uci.edu/ml/index.php上下载得到。首先读取Iris数据集，自行指定初始聚类中心调用前面编写的KMeans函数进行聚类，然后计算聚类的准确率，其代码如下

clear 
data=load('Iris.txt');
data=data(:,2:end);

matrix=[5.9016,2.7484,4.3935,1.4339;6.8500,3.0737,5.7421,2.0711;5.0060,3.4280,1.4620,0.2460];
[Idx,C,distance]=KMeans(data,3,matrix,500);
Distance=sum(distance)

c1=Idx(1:50,1);c2=Idx(51:100,1);c3=Idx(101:150,1);
accuracy=(sum(c1==mode(Idx(1:50,1)))+sum(c2==mode(Idx(51:100,1)))+sum(c3==mode(Idx(101:150,1))))/150

为方便使用Iris数据集经过了一些整理，这里将最后一列的带字符串的标签Iris-setosa，Iris-versicolor，Iris-virginica分别用数字1,2,3代替并移到了第一列，所以第三行选取的是从第二列至最后一列的数据。第5行中的matrix是查阅论文得到的一个初始聚类中心，正好用来比对聚类结果。第6行则调用KMeans()函数进行聚类，得到聚类标号和类内距离。对每类的类内距离求和即得到总的距离Distance，如第7行。准确率的计算有点麻烦，因为不能直接用KMeans计算后得到的标号跟原数据集中的标号对比计算准确率，KMeans只需要也只能将那些“相似”的数据点聚集到一类中，而给这一类数据的标号却是可能跟原数据集不同的。

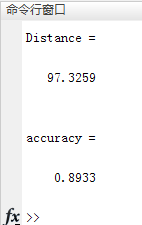
这里采用一个简单的方法，从原数据集的标签可以看出第1-50个数据点为一类（Iris-setosa），第51-100为一类（Iris-versicolor），第101-150为一类（Iris-virginica），因此只需确定每50个数据点中的聚类标号是不是一致。取它们之中数目最多的标号作为正确的个数，最终比上数据集的总数即为准确率。以上代码运行结果如下所示。

5. 类簇中心点的选取

KMeans算法本身思想比较简单，但是合理的确定K值和K个初始类簇中心点对于聚类效果的好坏有很大的影响。最简单的确定初始类簇中心点的方法是随机产生数据大小范围内的K个点作为初始的簇类中心点。随机产生初始点并进行测试的程序代码如下

clear
data=load('Iris.txt');
data=data(:,2:end);
K=3;


%% 产生随机初始点
[numOfData,numOfAttr]=size(data);   % numOfData是数据个数，numOfAttr是数据维数

centroids=zeros(K,numOfAttr);       % 随机初始化，最终迭代到每一类的中心位置
maxAttr=zeros(numOfAttr);        % 每一维最大的数
minAttr=zeros(numOfAttr);        % 每一维最小的数
for i=1:numOfAttr
    maxAttr(i)=max(data(:,i));    % 每一维最大的数
    minAttr(i)=min(data(:,i));    % 每一维最小的数
    for j=1:K
        centroids(j,i)=maxAttr(i)+(minAttr(i)-maxAttr(i))*rand();  % 随机初始化，选取每一维[min max]中初始化
    end
end

[Idx,C,distance]=KMeans(data,K,centroids,500);% 调用KMeans
Distance=sum(distance)% 计算类内距离之和

%% 计算准确率
c1=Idx(1:50,1);c2=Idx(51:100,1);c3=Idx(101:150,1);
Accuracy=(sum(c1==mode(Idx(1:50,1)))+sum(c2==mode(Idx(51:100,1)))+sum(c3==mode(Idx(101:150,1))))/numOfData

可以多运行几次以上代码，可以看出由于初始点事随机选取的每次运行得到的结果有所差异。这也是基本Kmeans算法的一个缺点，随着众多改进算法的提出Kmeans算法的这一问题也得到改善，深入了解的朋友可以查阅相关论文。

6. 结束语

本博文的完整MATLAB程序文件与整理好的数据集文件已经上传，详细可参考这篇文章：https://zhuanlan.zhihu.com/p/568780076。

由于编者能力有限，代码即使经过了多次校对，也难免会有疏漏之处。希望您能热心指出其中的错误，以便下次修改时能以一个更完美更严谨的样子，呈现在大家面前。同时如果有更好的实现方法也请您不吝赐教。

今天的文章Kmeans聚类算法详解分享到此就结束了，感谢您的阅读。