1. 编程号首页

C++——多项式拟合

编程小号 • • 未分类

C++——多项式拟合C++——多项式拟合目标：利用C++对txt或者xml中的数据，进行高阶或低阶多项式拟合为方便以后查找，代码以及详细资料已打包，并上传至云盘（链接：https://pan.baidu.com/

                                           C++——多项式拟合

目标：利用C++对txt或者xml中的数据，进行高阶或低阶多项式拟合

        为方便以后查找，代码以及详细资料已打包，并上传至云盘（链接：https://pan.baidu.com/s/1bvUBIoxv7Avxeq_Cz6xOZQ 密码：u9qe）

打包的内容如下：

C++——多项式拟合

 

C++——多项式拟合

 

C++——多项式拟合

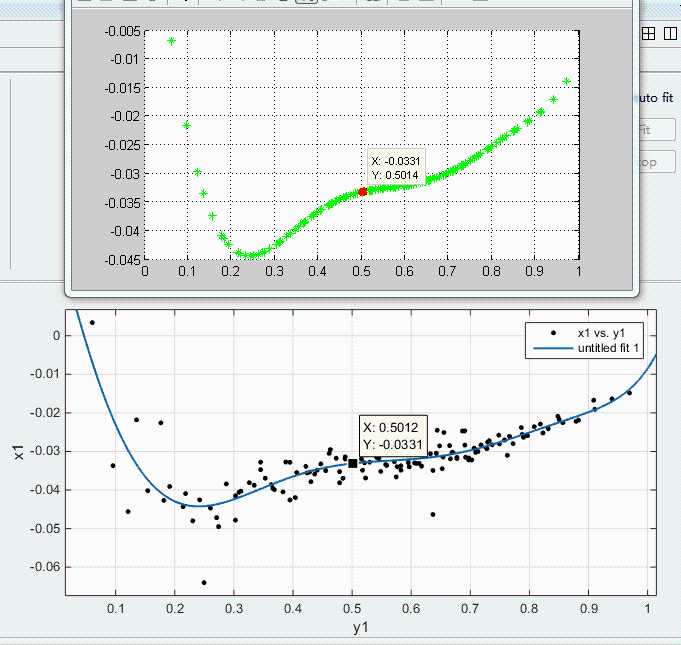
运行结果：

C++——多项式拟合

上图是C++代码运行的结果，在Matlab中显示的效果；下图是Matlab中利用Curve Fitting Tool拟合的效果（四阶多项式拟合）。注意横坐标与纵坐标不一样额，那是因为这里的原始数据与一般的数据不同：一个x坐标可能对应多个y值。这种情况直接将横纵坐标反着写就行了。

C++代码：

一、cpp文件

1、主函数curveFittingMain.cpp：

#include <iostream>
#include <fstream>
#include <Linequ.h>
#include <LS.h>
#include <Matrix.h>
#include <vector>
#include <fstream>
using namespace std;

vector<double> fitCurve(vector<double> arr_1, vector<double> arr_2, int n);
vector<double> getFitPoint(vector<double> coArr, vector<double> pointArr);

int main(int argc, char* argv[])
{
	//step1: 读取txt文件中的数据
	string file_x = "C:\\Users\\Zhangwei\\Desktop\\TEST\\多坐标点\\Quadrant_finalX.txt";
	string file_y = "C:\\Users\\Zhangwei\\Desktop\\TEST\\多坐标点\\Quadrant_finalY.txt";
	ifstream infile_x,infile_y;
	infile_x.open(file_x);
	infile_y.open(file_y);
	if (!infile_x && !infile_y) 
		cout << "error" << endl;

	double temp;
	vector<double> Data_x, Data_y;
	while (infile_x >> temp)
	{
		Data_x.push_back(temp);
	}
	while (infile_y >> temp)
	{
		Data_y.push_back(temp);
	}

	//step2:调用拟合函数
         // CoArr 表示多项式拟合的系数
         // myRes 表示拟合的系数与拟合前的横坐标，计算得到新的纵坐标
	vector<double> CoArr = fitCurve(Data_y, Data_x, 4); //调用函数，4表示阶数，（可以随意取，1—线性拟合，2—平方拟合，3—立方拟合,>=4,高阶拟合）
	vector<double> myRes = getFitPoint(CoArr, Data_y); //生成拟合数据

	//step3:将myRes保存为txt文档
	ofstream outfile;
	outfile.open("C:\\Users\\Zhangwei\\Desktop\\TEST\\多坐标点\\Quadrant_Final.txt");
	for (int j = 0; j < myRes.size(); j++)
	{
		outfile << myRes[j] << endl;
	}
	outfile.close();

	//system("pause");
	return 0;
}


//getFitPoint函数用于获取拟合后的数据点
vector<double> getFitPoint(vector<double> coArr, vector<double> pointArr)
{
	vector<double> finalPoint;
	if (pointArr.size() == 0 || coArr.size() == 0)
	{
		cout << "数据点有误！" << endl;
	}
	if (pointArr.size() > 0 && coArr.size() > 0)
	{
		for (int i = 0; i < pointArr.size(); i++)
		{
			double temp = 0;
			for (int j = 0; j < coArr.size(); j++)
			{
				temp += pow(pointArr[i], j)*coArr[j];
			}
			finalPoint.push_back(temp);
		}
	}
	return finalPoint;
}

//fitCurve函数用于曲线拟合
vector<double> fitCurve(vector<double> arr_1, vector<double> arr_2, int n)
{
	CLS m_cls;
	vector<double> coefficientsSet;
	if (arr_1.size() != arr_2.size())
	{
		cout << " 输入数据有误！" << endl;
	}
	if (arr_1.size() == arr_2.size())
	{
		for (int i = 0; i < arr_1.size(); i++)
		{
			m_cls.addPoint(arr_1[i], arr_2[i]);
		}
		m_cls.setN(n);
		m_cls.Solve();
		double *t_paracof = m_cls.getSolution();
		for (int i = 0; i < n + 1; i++)
		{
			coefficientsSet.push_back(t_paracof[i]); //多项式的系数项，第一项为常数项，最后一项为x^n项
		}
	}
	return coefficientsSet;
}

2、Linequ.cpp

// Linequ.cpp: implementation of the CLinequ class.
//
//

//#include "stdafx.h"
#include "math.h"
#include "Linequ.h"

#ifdef _DEBUG
#undef THIS_FILE
static char THIS_FILE[] = __FILE__;
//#define new DEBUG_NEW
#endif

//
// Construction/Destruction
//

CLinequ::CLinequ(int dims)
{
	index = dims;
	sums = new double[dims];
	MatrixA = new double[dims * dims];
	solu = new double[dims];
}

CLinequ::~CLinequ()
{
	delete[] sums;
	delete[] MatrixA;
	delete[] solu;
}

void CLinequ::setMatrix(double *rmatr)                   //设置矩阵
{
	for (int i = 0; i<index*index; i++){
		*(MatrixA + i) = rmatr[i];                          //矩阵成员赋初值
	}
}

void CLinequ::setLinequ(double *a, double *b)             //设置线性方程组
{
	setMatrix(a);                                       //调用基类函数
	for (int i = 0; i<index; i++)
		sums[i] = b[i];
}

int CLinequ::Solve()                                     //全选主元高斯消去法求解方程
{
	int *js, l, k, i, j, is, p, q;
	double d, t;
	js = new int[index];
	l = 1;
	for (k = 0; k <= index - 2; k++){                             //消去过程
		d = 0.0;
		for (i = k; i <= index - 1; i++)
			for (j = k; j <= index - 1; j++){
				t = fabs(MatrixA[i*index + j]);
				if (t>d)
				{
					d = t; js[k] = j; is = i;
				}
			}
		if (d + 1.0 == 1.0) l = 0;
		else
		{
			if (js[k] != k)
				for (i = 0; i <= index - 1; i++){
					p = i*index + k; q = i*index + js[k];
					t = MatrixA[p]; MatrixA[p] = MatrixA[q]; MatrixA[q] = t;
				}
			if (is != k)
			{
				for (j = k; j <= index - 1; j++){
					p = k*index + j; q = is*index + j;
					t = MatrixA[p]; MatrixA[p] = MatrixA[q]; MatrixA[q] = t;
				}
				t = sums[k]; sums[k] = sums[is]; sums[is] = t;
			}
		}
		if (l == 0)
		{
			delete[] js;
			//fail to solve
			return(0);
		}
		d = MatrixA[k*index + k];
		for (j = k + 1; j <= index - 1; j++){
			p = k*index + j; MatrixA[p] = MatrixA[p] / d;
		}
		sums[k] = sums[k] / d;
		for (i = k + 1; i <= index - 1; i++){
			for (j = k + 1; j <= index - 1; j++){
				p = i*index + j;
				MatrixA[p] = MatrixA[p] - MatrixA[i*index + k] * MatrixA[k*index + j];
			}
			sums[i] = sums[i] - MatrixA[i*index + k] * sums[k];
		}
	}
	d = MatrixA[(index - 1)*index + index - 1];
	if (fabs(d) + 1.0 == 1.0)
	{
		delete[] js;
		//fail to solve
		return(0);
	}
	solu[index - 1] = sums[index - 1] / d;                               //回代过程
	for (i = index - 2; i >= 0; i--){
		t = 0.0;
		for (j = i + 1; j <= index - 1; j++)
			t = t + MatrixA[i*index + j] * solu[j];
		solu[i] = sums[i] - t;
	}
	js[index - 1] = index - 1;
	for (k = index - 1; k >= 0; k--)
		if (js[k] != k)
		{
			t = solu[k]; solu[k] = solu[js[k]]; solu[js[k]] = t;
		}
	delete[] js;
	return(1);
}

double *CLinequ::getSolution() const
{
	return solu;
}

3、LS.cpp

// LS.cpp: implementation of the CLS class.
//
//

//#include "stdafx.h"
#include "LS.h"
#include "Matrix.h"
#include "Linequ.h"

#ifdef _DEBUG
#undef THIS_FILE
static char THIS_FILE[] = __FILE__;
//#define new DEBUG_NEW
#endif

//
// Construction/Destruction
//

CLS* CLS::_instance = 0;

CLS::CLS()
{
	pSolution = 0;
	m = 0;
	n = 0;
	_instance = this;
}

CLS::~CLS()
{
	if (pSolution)
		delete[] pSolution;
}

CLS *CLS::getInstance()
{
	if (!_instance)
		new CLS();
	return _instance;
}

void CLS::setN(int t)
{
	n = t + 1;
	if (pSolution)
		delete[] pSolution;
	pSolution = new double[n];
}

void CLS::addPoint(double x, double y)
{
	pVertex[m][0] = x;
	pVertex[m][1] = y;
	m++;
}

bool CLS::Solve()
{
	if (m <= 0 || n <= 0)
		return false;
	CMatrix *A = new CMatrix(m, n);
	int i, j;
	for (j = 0; j < m; j++)
		A->setData(j, 0, 1.0);
	for (i = 1; i < n; i++)
	{
		for (j = 0; j < m; j++)
		{
			A->setData(j, i, A->getData(j, i - 1) * pVertex[j][0]);
		}
	}
	CMatrix *B = A->getRev();
	CMatrix *b = new CMatrix(m, 1);
	for (i = 0; i < m; i++)
		b->setData(i, 0, pVertex[i][1]);
	CMatrix *C = B->getMul(A);
	CMatrix *d = B->getMul(b);

	CLinequ *pL = new CLinequ(n);
	pL->setLinequ(C->getMatrix(), d->getMatrix());
	pL->Solve();
	double *t = pL->getSolution();
	for (i = 0; i < n; i++)
		pSolution[i] = t[i];

	return true;
}

double *CLS::getSolution() const
{
	return pSolution;
}

double CLS::calcY(double x)
{
	double y = 0.0, temp = 1.0;
	for (int i = 0; i < n; i++)
	{
		y += pSolution[i] * temp;
		temp *= x;
	}
	return y;
}

void CLS::restart()
{
	m = 0;
	if (pSolution)
		delete[] pSolution;
	pSolution = 0;
	n = 0;
}

4、Matrix.cpp

// Matrix.cpp: implementation of the CMatrix class.
//
//

//#include "stdafx.h"
#include "Matrix.h"

#ifdef _DEBUG
#undef THIS_FILE
static char THIS_FILE[] = __FILE__;
//#define new DEBUG_NEW
#endif

//
// Construction/Destruction
//

void CMatrix::setMatrix(double *rmatr)                   //设置矩阵
{
	for (int i = 0; i < m * n; i++)
	{
		*(pMatrix + i) = rmatr[i];                          //矩阵成员赋初值
	}
}

CMatrix::CMatrix(int a, int b)                               //矩阵Matrix类的构造函数
{
	m = a; n = b;                                         //保护数据赋值
	pMatrix = new double[m * n];                    //动态分配内存
}

CMatrix::~CMatrix()                                       //矩阵Matrix类的析构函数
{
	delete[] pMatrix;                                   //内存释放
}

CMatrix *CMatrix::getRev()
{
	CMatrix *pR = new CMatrix(n, m);
	for (int j = 0; j < n; j++)
	{
		for (int i = 0; i < m; i++)
			*(pR->pMatrix + i + m * j) = *(pMatrix + i * n + j);
	}
	return pR;
}

CMatrix *CMatrix::getMul(CMatrix *b)
{
	if (b->m != n)
		return 0;
	CMatrix *pR = new CMatrix(m, b->n);
	for (int i = 0; i < m; i++)
	{
		for (int j = 0; j < b->n; j++)
		{
			double temp = 0.0;
			for (int k = 0; k < n; k++)
				temp += *(pMatrix + i * n + k) * *(b->pMatrix + k * b->n + j);
			*(pR->pMatrix + i * b->n + j) = temp;
		}
	}

	return pR;
}

int CMatrix::getM() const
{
	return m;
}

int CMatrix::getN() const
{
	return n;
}

double *CMatrix::getMatrix() const
{
	return pMatrix;
}

double CMatrix::getData(int i, int j) const
{
	if (i < m && j < n && i >= 0 && j >= 0)
		return *(pMatrix + i * n + j);
	else
		return 0.0;
}

void CMatrix::setData(int i, int j, double t)
{
	if (i < m && j < n && i >= 0 && j >= 0)
	{
		*(pMatrix + i * n + j) = t;
	}
}

二、头文件（.h文件）

1、Linequ.h

// Linequ.h: interface for the CLinequ class.
//
//

#if !defined(AFX_LINEQU_H__3673E7FC_1154_436A_9D22_B472DD858F13__INCLUDED_)
#define AFX_LINEQU_H__3673E7FC_1154_436A_9D22_B472DD858F13__INCLUDED_

#if _MSC_VER > 1000
#pragma once
#endif // _MSC_VER > 1000

class CLinequ
{
public:                                   //外部接口
	CLinequ(int dims = 2);                   //构造函数
	virtual ~CLinequ();                            //析构函数
	void setLinequ(double *a, double *b);  //方称赋值
	void setMatrix(double *rmatr);
	int Solve();                          //全选主元高斯消去法求解方程
	double *getSolution() const;

private:
	double *sums;                         //方程右端项
	double *MatrixA;
	double *solu;                         //方程的解
	int index;
};

#endif // !defined(AFX_LINEQU_H__3673E7FC_1154_436A_9D22_B472DD858F13__INCLUDED_)

2、LS.h

// LS.h: interface for the CLS class.
//
//

#if !defined(AFX_LS_H__208D279A_F391_4DA8_BBE3_3895A9800FFE__INCLUDED_)
#define AFX_LS_H__208D279A_F391_4DA8_BBE3_3895A9800FFE__INCLUDED_

#if _MSC_VER > 1000
#pragma once
#endif // _MSC_VER > 1000

class CLS
{
private:
	static CLS *_instance;

	double pVertex[2000][2];//最多可以拟合2000个点
	int m;	//点的个数
	int n;	//多项式次数
	double *pSolution;	//多项式系数

public:
	CLS();
	virtual ~CLS();
	static CLS *getInstance();



	void setN(int t);	//n次多项式拟合
	void addPoint(double x, double y);	//添加一个点
	void restart();

	bool Solve();
	double *getSolution() const;	//获得多项式系数
	double calcY(double x);	//根据x坐标计算y
};

#endif // !defined(AFX_LS_H__208D279A_F391_4DA8_BBE3_3895A9800FFE__INCLUDED_)

3、Matrix.h

// Matrix.h: interface for the CMatrix class.
//
//

#if !defined(AFX_MATRIX_H__AEE89FA3_05E2_44AC_AA96_5FBCB3608C13__INCLUDED_)
#define AFX_MATRIX_H__AEE89FA3_05E2_44AC_AA96_5FBCB3608C13__INCLUDED_

#if _MSC_VER > 1000
#pragma once
#endif // _MSC_VER > 1000

class CMatrix
{
public:
	CMatrix(int a = 2, int b = 2);
	virtual ~CMatrix();
	void setMatrix(double *rmatr);

	CMatrix *getRev();
	CMatrix *getMul(CMatrix *b);

	int getM() const;	//获得行数
	int getN() const;	//获得列数
	double getData(int i, int j) const;
	void setData(int i, int j, double t);
	double *getMatrix() const;	//获得矩阵

protected:
	int m, n;
	double *pMatrix;
};

#endif // !defined(AFX_MATRIX_H__AEE89FA3_05E2_44AC_AA96_5FBCB3608C13__INCLUDED_)

 

今天的文章C++——多项式拟合分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/72770.html

赞 (0)
编程小号编程小号
0

相关推荐

发表回复

您的电子邮箱地址不会被公开。 必填项已用*标注