gelu激活函数怎么读_relu和silu的区别

Gaussian Error Linerar Units(GELUS)

论文链接：https://arxiv.org/abs/1606.08415
最近在看bert源码，发现里边的激活函数不是Relu等常见的函数，是一个新的激活函数GELUs, 这里记录分析一下该激活函数的特点。

不管其他领域的鄙视链，在激活函数领域，大家公式的鄙视链应该是：Elus > Relu > Sigmoid ，这些激活函数都有自身的缺陷， sigmoid容易饱和，Elus与Relu缺乏随机因素。

在神经网络的建模过程中，模型很重要的性质就是非线性，同时为了模型泛化能力，需要加入随机正则，例如dropout(随机置一些输出为0,其实也是一种变相的随机非线性激活)， 而随机正则与非线性激活是分开的两个事情， 而其实模型的输入是由非线性激活与随机正则两者共同决定的。

GELUs正是在激活中引入了随机正则的思想，是一种对神经元输入的概率描述，直观上更符合自然的认识，同时实验效果要比Relus与ELUs都要好。

GELUs其实是 dropout、zoneout、Relus的综合，GELUs对于输入乘以一个0,1组成的mask，而该mask的生成则是依概率随机的依赖于输入。假设输入为X, mask为m，则m服从一个伯努利分布($\Phi (x)$, $\Phi (x)=P(X<=x),X服从标准正太分布$)，这么选择是因为神经元的输入趋向于正太分布，这么设定使得当输入x减小的时候，输入会有一个更高的概率被dropout掉，这样的激活变换就会随机依赖于输入了。
数学表达如下：
$$GELU(x)=xP(X<=x)=x\Phi (x)$$
这里$\Phi (x)$是正太分布的概率函数，可以简单采用正太分布$\mathbb{N}(0,1)$, 要是觉得不刺激当然可以使用参数化的正太分布$\mathbb{N}(\mu ,\sigma )$, 然后通过训练得到$\mu ,\sigma$。

对于假设为标准正太分布的$GELU(x)$, 论文中提供了近似计算的数学公式，如下：
$$GELU(x)=0.5x(1+tanh[\sqrt{2/\pi }(x+0.044715x^3)])$$
翻看bert源码给出的GELU代码表示如下：

def gelu(input_tensor):
	cdf = 0.5 * (1.0 + tf.erf(input_tensor / tf.sqrt(2.0)))
	return input_tesnsor*cdf

感觉bert源码中的近似计算更简单，具体怎么近似的，我猜不出来。

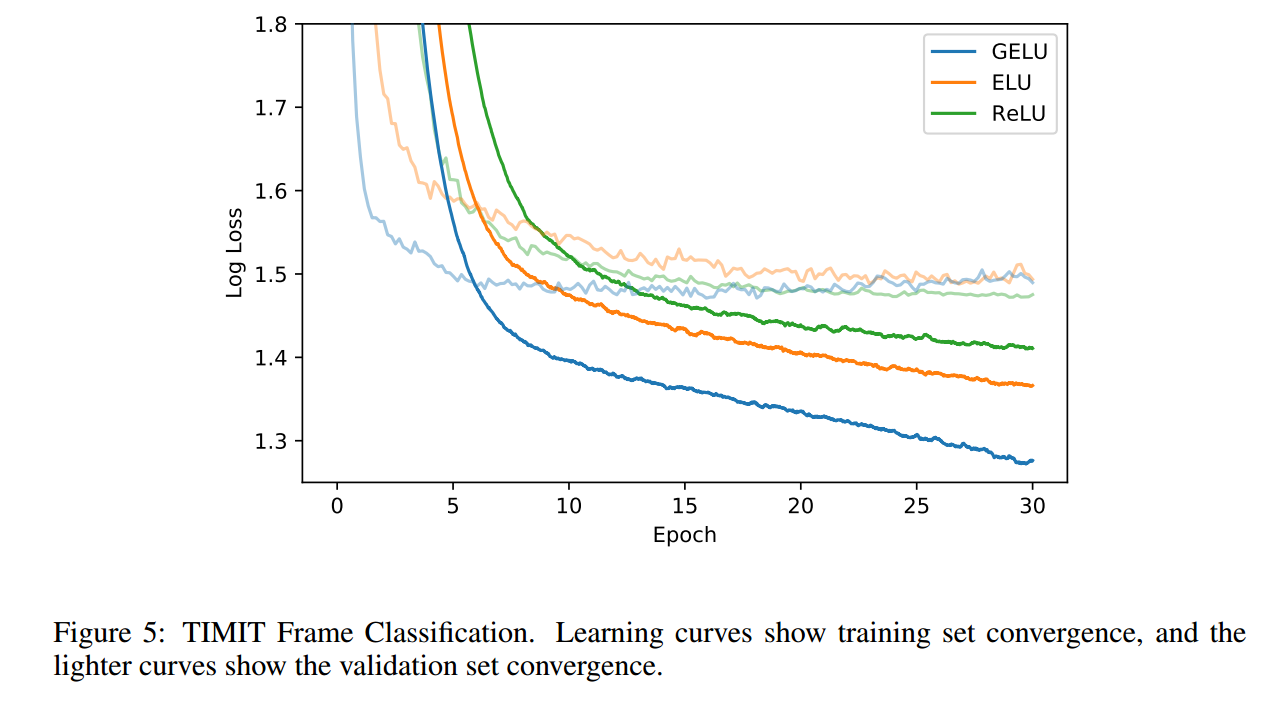
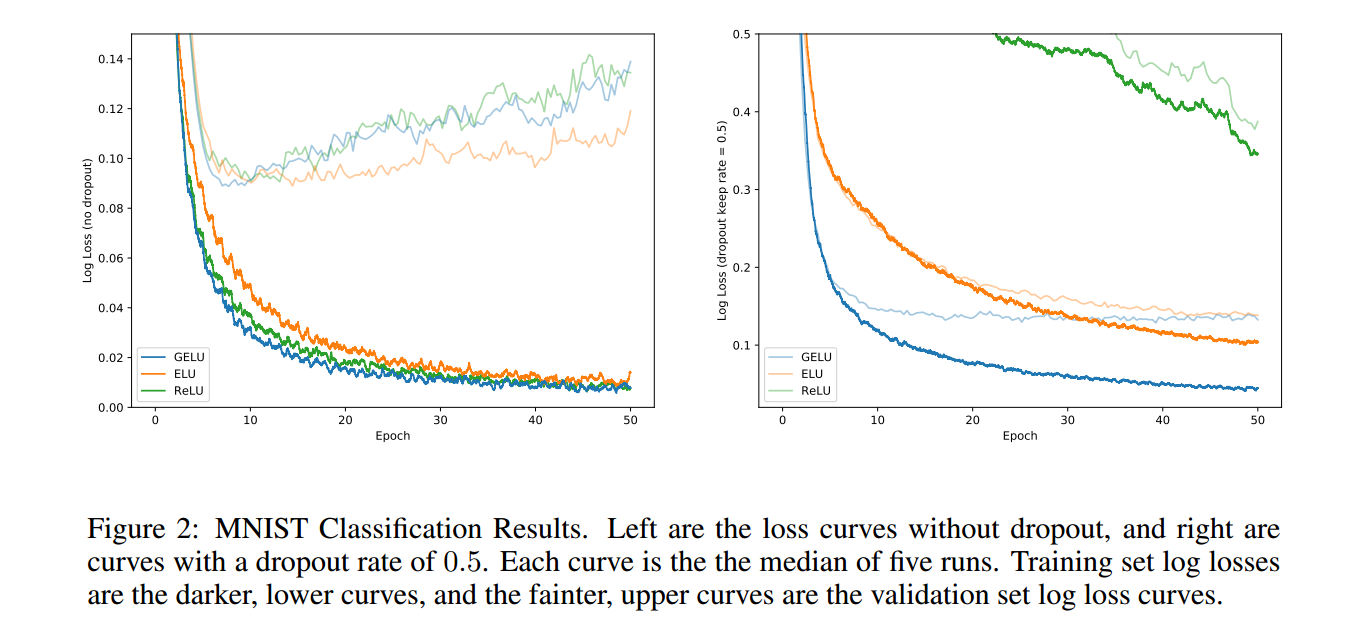
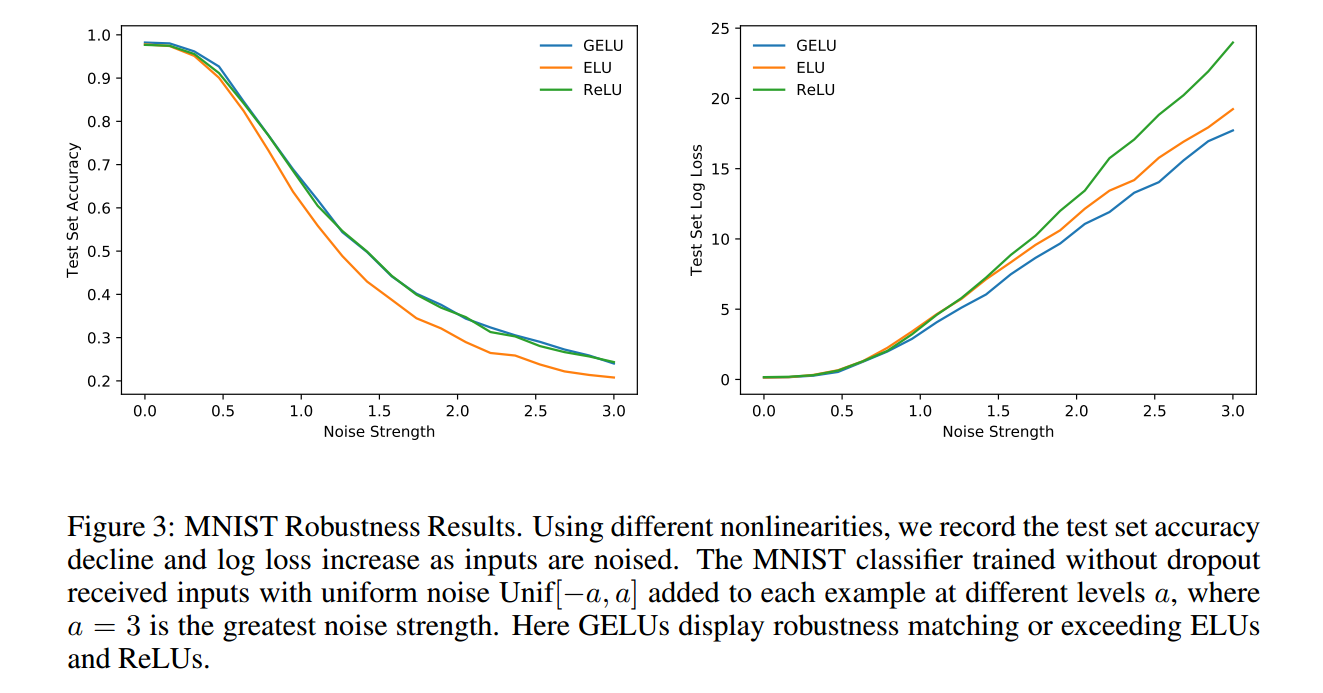
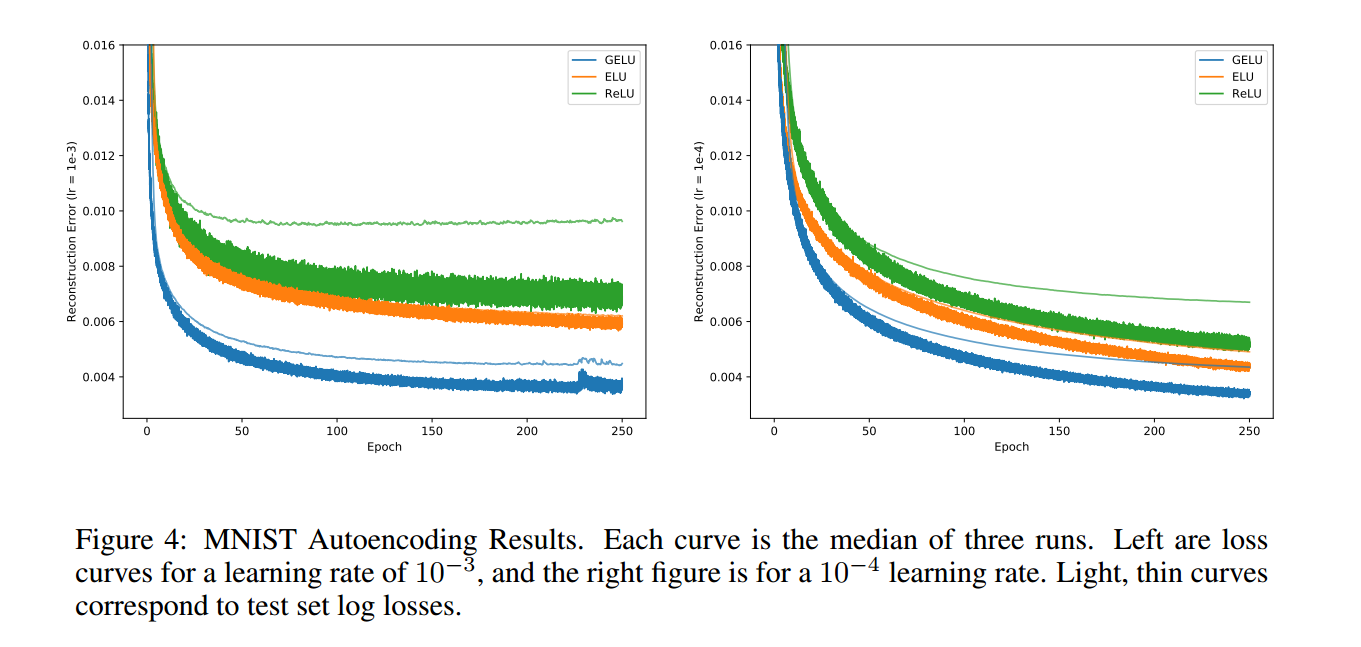
下面贴一些论文的实验图，就是证明GELU学习更快且更好：

今天的文章gelu激活函数怎么读_relu和silu的区别分享到此就结束了，感谢您的阅读。