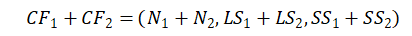1.作者介绍

冯达，男，西安工程大学电子信息学院，2021级研究生
研究方向：控制科学与工程
电子邮件：845907526@qq.com

刘帅波，男，西安工程大学电子信息学院，2021级研究生，张宏伟人工智能课题组
研究方向：机器视觉与人工智能
电子邮件：1461004501@qq.com

2.BIRCH聚类算法介绍

2.1 BIRCH聚类算法介绍

BIRCH的全称是利用层次方法的平衡迭代规约和聚类（Balanced Iterative Reducing and Clustering Using Hierarchies），它是用层次方法来聚类和规约数据。
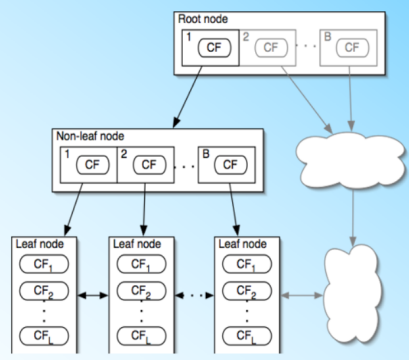
BIRCH算法利用了一个树结构来帮助我们快速的聚类，这个树结构称之为聚类特征树(Clustering Feature Tree，简称CF Tree)。这颗树的每一个节点是由若干个聚类特征(Clustering Feature，简称CF)组成。从右图中我们可以看看聚类特征树的样子：每个节点包括叶子节点都有若干个CF，而内部节点的CF有指向孩子节点的指针，所有的叶子节点用一个双向链表链接起来。
将所有的训练集样本建立了CF Tree，一个基本的BIRCH算法就完成了，对应的输出就是若干个CF节点，每个节点里的样本点就是一个聚类的簇。也就是说BIRCH算法的主要过程，就是建立CF Tree的过程。

2.2 聚类特征CF与聚类特征树CF Tree

聚类特征CF：
在聚类特征树中，一个聚类特征CF是这样定义的：每一个CF是一个三元组，可以用（N，LS，SS）表示。
N代表了这个CF中拥有的样本点的数量
LS代表了这个CF中拥有的样本点各特征维度的和向量；
SS代表了这个CF中拥有的样本点各特征维度的平方和；
CF有一个很好的性质，就是满足线性关系，也就是：

把这个性质放在CF Tree上，那么对于每个父节点中的CF节点，它的（N，LS，SS）三元组的值等于这个CF节点所指向的所有子节点的三元组之和。
聚类特征树CF Tree：
对于CF Tree，我们一般有几个重要参数，第一个参数是每个内部节点的最大CF数B，第二个参数是每个叶子节点的最大CF数L，第三个参数是针对叶子节点中某个CF中的样本点来说的，它是叶节点每个CF的最大样本半径阈值T，也就是说，在这个CF中的所有样本点一定要在半径小于T的一个超球体内。

2.3 Birch聚类算法优缺点

优点：
(1）节约内存，所有的样本都在磁盘上，CF Tree仅仅存了CF节点和对应的指针。
(2）聚类速度快，只需要一遍扫描训练集就可以建立CF Tree，CF Tree的增删改都很快。
(3）可以识别噪音点，还可以对数据集进行初步分类的预处理。
缺点：
(1）由于CF Tree对每个节点的CF个数有限制，导致聚类的结果可能和真实的类别分布不同。
(2）对高维特征的数据聚类效果不好。此时可以选择Mini Batch K-Means。
(3）如果数据集的分布簇不是类似于超球体，或者说不是凸的，则聚类效果不好。

3.scikit-learn学习Birch聚类

3.1 Brich类参数

在scikit-learn中，BIRCH类实现了基于特征树CF Tree的聚类，其中重要参数主要有以下几个：
threshold：即叶节点每个CF的最大样本半径阈值T，它决定了每个CF里所有样本形成的超球体的半径阈值。一般来说threshold越小，则CF Tree的建立阶段的规模会越大，即BIRCH算法第一阶段所花的时间和内存会越多。但是选择多大以达到聚类效果则需要通过调参决定。默认值是0.5.如果样本的方差较大，则一般需要增大这个默认值。
branching_factor:即CF Tree内部节点的最大CF数B，以及叶子节点的最大CF数L。这里scikit-learn对这两个参数进行了统一取值。也就是说，branching_factor决定了CF Tree里所有节点的最大CF数。默认是50。如果样本量非常大，比如大于10万，则一般需要增大这个默认值。选择多大的branching_factor以达到聚类效果则需要通过和threshold一起调参决定。
n_clusters：即类别数K，在BIRCH算法是可选的，如果类别数非常多，我们也没有先验知识，则一般输入None，此时BIRCH算法第4阶段不会运行。但是如果我们有类别的先验知识，则推荐输入这个可选的类别值。默认是3，即最终聚为3类。
compute_labels：布尔值，表示是否标示类别输出，默认是True。一般使用默认值挺好，这样可以看到聚类效果。
在评估各个参数组合的聚类效果时，如果不知道真实的标签,Calinski-Harabasz指数——方差比准则,可以用来评估模型，更高的Calinski-Harabasz得分表示该聚类的模型越好。

4.实验代码与结果展示

4.1 完整代码

import matplotlib.pyplot as plt#导入matplotlib库
from sklearn.datasets import make_blobs #导入数据集
from sklearn.cluster import Birch#导入Birch类
from sklearn import metrics#调用评价指标

# X为样本特征，Y为样本簇类别， 共1000个样本，每个样本2个特征，共4个簇，簇中心在[-1,-1], [0,0],[1,1], [2,2]
# 每个类别的方差分别为0.4, 0.3, 0.4, 0.3
X, y = make_blobs(n_samples=1000, n_features=2,
                  centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
                  cluster_std=[0.4, 0.3, 0.4, 0.3], random_state=9)

# 设置参数：尝试多个threshold取值，和多个branching_factor取值
param_grid = { 
   'threshold': [0.1, 0.3, 0.5],
              'branching_factor': [10, 20, 50]}

CH_all = []
X_all = []
y_all = []
paras_all = []

# 开始聚类
for threshold in param_grid['threshold']:
    for branching_factor in param_grid['branching_factor']:
        ##设置birch函数
        birch = Birch(n_clusters=4, threshold = threshold, branching_factor = branching_factor)
        #实现拟合
        birch.fit(X)
        X_all.append(X)
        #实现预测
        y_pred = birch.predict(X)
        y_all.append(y_pred)
        #生成评价指标
        CH = metrics.calinski_harabasz_score(X, y_pred)
        CH_all.append(CH)
        paras_all.append([threshold, branching_factor])
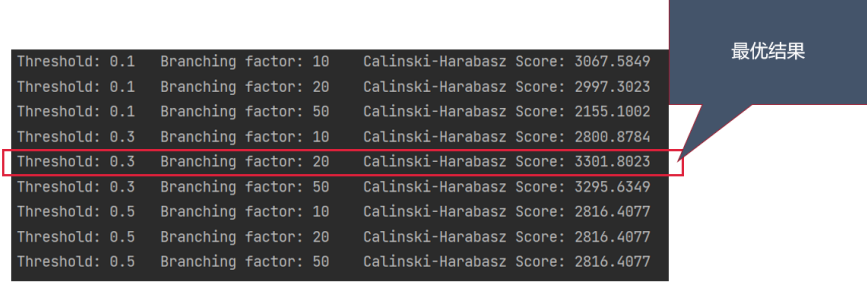
        print("Threshold:", threshold, "\t",
              "Branching factor:", branching_factor, "\t",
              "Calinski-Harabasz Score:", '%.4f' %CH)


# 挑选并存储最优的解
CH_max = max(CH_all)
idx = CH_all.index(CH_max)
X_max = X_all[idx]
y_max = y_all[idx]

# 绘制数据分布图
plt.figure() # 创建图像
plt.subplot(1, 2, 1)    # subplot创建单个子图，单个字图中包含2个区域，相应区域在左侧
plt.scatter(X[:, 0], X[:, 1], marker='.', c = y) # 画散点图
plt.title('Original Cluster Plot')  # 将图命名
plt.xlabel('(1)')   #设置X轴的标签为（1）

plt.subplot(1, 2, 2) # subplot创建单个子图，单个字图中包含2个区域，相应区域在右侧
plt.scatter(X_max[:, 0], X_max[:, 1], marker='.', c=y_max)  # 画散点图
plt.title('Result (Threshold = ' + str(paras_all[idx][0])
          + ', BF = ' + str(paras_all[idx][1]) + ')')   # 将图命名
plt.xlabel('(2)')   #设置X轴的标签为（1）

plt.show()

4.2 实现过程

（1）导入实验环境所需要的包

import matplotlib.pyplot as plt#导入matplotlib库
from sklearn.datasets import make_blobs #导入数据集
from sklearn.cluster import Birch#导入Birch类
from sklearn import metrics#调用评价指标

（2）导入实验所需要的随机数据

# X为样本特征，Y为样本簇类别， 共1000个样本，每个样本2个特征，共4个簇，簇中心在[-1,-1], [0,0],[1,1], [2,2]
# 每个类别的方差分别为0.4, 0.3, 0.4, 0.3
X, y = make_blobs(n_samples=1000, n_features=2,
                  centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
                  cluster_std=[0.4, 0.3, 0.4, 0.3], random_state=9)

（3）设置多个threshold和branching_factor

# 设置参数：尝试多个threshold取值，和多个branching_factor取值
param_grid = { 
   'threshold': [0.1, 0.3, 0.5],
              'branching_factor': [10, 20, 50]}

（4）开始Birch聚类

# 开始聚类
for threshold in param_grid['threshold']:
    for branching_factor in param_grid['branching_factor']:
        ##设置birch函数
        birch = Birch(n_clusters=4, threshold = threshold, branching_factor = branching_factor)
        #实现拟合
        birch.fit(X)
        X_all.append(X)
        #实现预测
        y_pred = birch.predict(X)
        y_all.append(y_pred)
        #生成评价指标
        CH = metrics.calinski_harabasz_score(X, y_pred)
        CH_all.append(CH)
        paras_all.append([threshold, branching_factor])
        print("Threshold:", threshold, "\t",
              "Branching factor:", branching_factor, "\t",
              "Calinski-Harabasz Score:", '%.4f' %CH)

（5）绘制数据分布图

# 绘制数据分布图
plt.figure() # 创建图像
plt.subplot(1, 2, 1)    # subplot创建单个子图，单个字图中包含2个区域，相应区域在左侧
plt.scatter(X[:, 0], X[:, 1], marker='.', c = y) # 画散点图
plt.title('Original Cluster Plot')  # 将图命名
plt.xlabel('(1)')   #设置X轴的标签为（1）

plt.subplot(1, 2, 2) # subplot创建单个子图，单个字图中包含2个区域，相应区域在右侧
plt.scatter(X_max[:, 0], X_max[:, 1], marker='.', c=y_max)  # 画散点图
plt.title('Result (Threshold = ' + str(paras_all[idx][0])
          + ', BF = ' + str(paras_all[idx][1]) + ')')   # 将图命名
plt.xlabel('(2)')   #设置X轴的标签为（1）

plt.show()

4.3 实验结果

今天的文章Birch聚类算法的实现分享到此就结束了，感谢您的阅读。