目录
在得到相关数据资料后,我们要对这些数据进行分析,研究各个变量之间的关系。相关分析是应用非常广泛的一种方法。它是不考虑变量之间的因果关系而只研究分析变量之间的相关关系的一种统计分析方法,常用的相关分析包括简单相关分析、偏相关分析等。
7.1简单相关分析
数据(案例7.1)
对数据的月份、温度、日照时间三个变量进行简单相关性分析,命令如下:
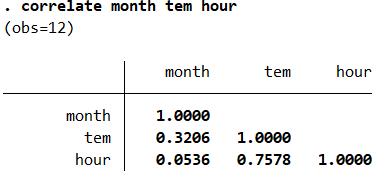
correlate month tem hour结果如图所示,我们可以看到有12个样本参与了分析(obs=12)然后可以看到变量之间的相关系数,其中month与tem的相关系数是0.3206,month与hour的的相关系数是0.0536,tem与hour的相关系数是0.7578。这个相关系数越大说明两个变量之间的关系越紧密,也就是说平均温度和日照时间具有比较高的相关性。
案例延伸:
1.获得变量的协方差矩阵
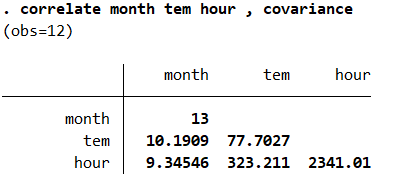
correlate month tem hour,covariance结果如图所示,我们可以看到变量的协方差矩阵,其中month的方差是13,tem的方差是77.7027,hour的方差是2341.01,month与tem的协方差是10.1909,month与hour的协方差是9.34546,tem与hour的协方差是323.211。这个两个变量之间的协方差也是代表了两个变量之间的相关性,值越高相关性越高。
2.获得相关性的显著性检验
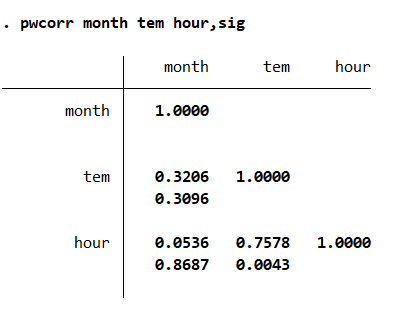
pwcorr month tem hour,sig结果如图所示,其中,month与tem之间的相关性显著性P值是0.3096,month与hour之间的相关性显著性P值是0.8687,tem与hour的相关性显著性P值是0.0043。显著性检验在前面的章节也说过,在这我们假设他们是相关性不大,P值大于0.05则支持了咱们的假设,P值小于0.05则推翻假设。这里明显看出tem与hour推翻假设说明两个变量之间相关性很强。
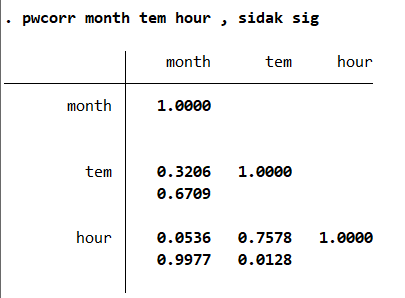
此外还有一种更为精准的sidak方法。命令如下
pwcorr month tem hour,sidak sig这个同上个结论相同这里不多赘述了。只不过是更加精确了而已。
3.获得相关性的显著性检验,并进行标注
很多时候我们希望能够一目了然的看出变量相关在不同置信水平上是否显著例如置信水平为99%的时候,对应命令如下
pwcorr month tem hour ,sidak sig star(0.01)置信水平为90%的时候,对应命令如下
pwcorr month tem hour ,sidak sig star(0.1)结果就不再过多赘述了。
7.2偏相关分析
很多情况下,需要进行相关分析的变量的取值会同时收到其他变量的影响,这时就需要把其他变量控制住,然后输出控制其他变量影响后的相关系数。
数据(案例7.2)
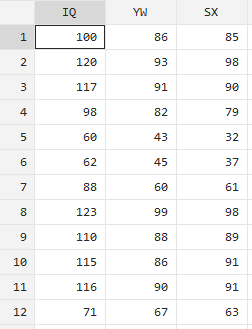
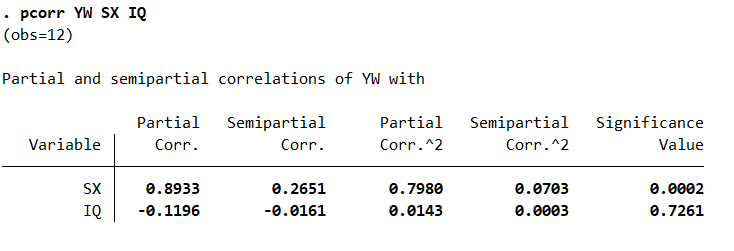
pcorr YW SX IQ结果如图所示,我们可以看出一共有12个样本参与了方差分析,在控制住IQ变量的情况下,语文成绩和数学成绩的偏相关系数(Paertial Corr)是0.8933–系数越大说明两个变量之间影响越小,显著性水平(Significance Value)是0.0002–小于0.05说明两个变量之间影响越大,大于0.05说明两个变量之间影响越小。此外,该结果还给出了控制数学成绩变量的情况下,语文成绩和IQ之间的偏相关关系,他们的偏相关系数是-0.1196,显著性水平是0.7261。在这个数据中可以看出数学成绩和语文成绩在控制IQ变量的情况下相关性还是很强的(可能现实不是那样但是这个数据中就是如此)。
案例延伸
1.部分数据进行偏相关分析
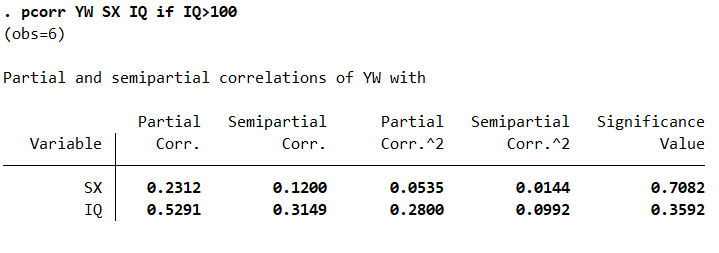
pcorr YW SX IQ if IQ>100结果如图所示,与上述结果有所不同,在控制了IQ>100的前提下我们可以看到语文成绩和数学成绩之间的相关性很弱。
今天的文章stata相关性分析结果解读_相关性分析有哪些方法分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/74230.html