史上最详细的MFCC算法实现(附测试数据)
1.matlab安装voicebox语音包
这里该包的安装我直接附上我们师姐写过的一篇文章,里边的介绍很详细:
戳这里!!!跳转到文章链接地址
2.MFCC原理讲解
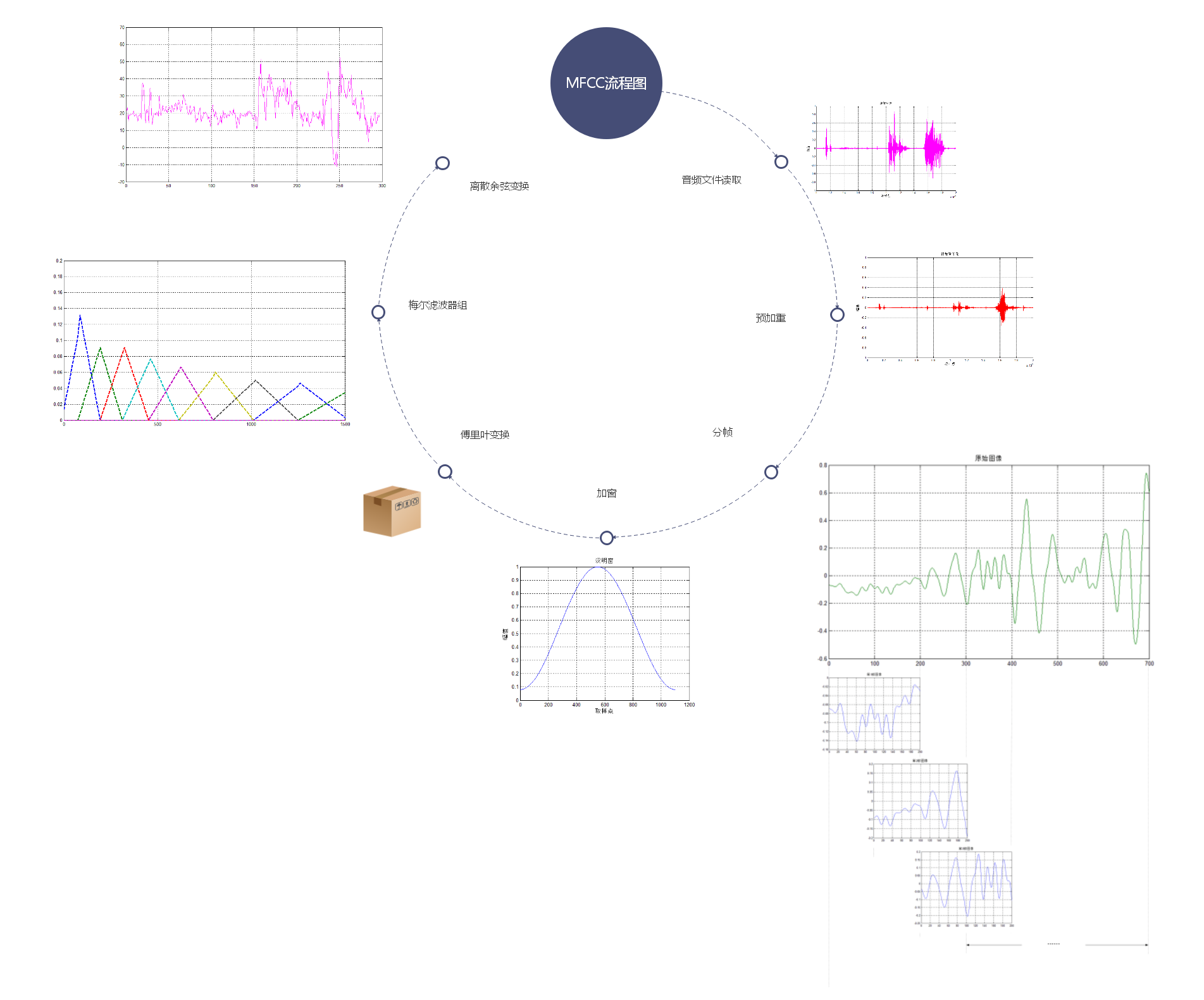
整个MFCC过程大致可以分为以下几步:
1.音频文件读取(最好是.wav文件)
2.预先加重
3.分帧
4.加窗
5.傅里叶变换(当是2的N次方时,可以使用FFT快速傅里叶变换)
6.梅尔滤波器组
7.离散余弦变换DCT
3.MFCC算法设计实现(matlab)
3.1 .wav格式语音文件提取【x(200000*1)】
\qquad 在matlab中,使用函数audioread函数来读取本地wav文件,这里要注意的是,采样频率一般为8000Hz和16000Hz,采样频率需要大于真实信号最大频率的2倍,才不会导致频谱混叠。
clc;
clear;
[x,fs]=audioread('diguashao.wav');%读取wav文件
这里我们用于测试的数据的采样频率 f s f_s fs 44100,这个是由 audioread函数默认决定的。
3.2 预加重【x(200000*1)】
\qquad 为了避免在后边的FFT操作中出现数值问题,我们需要加强一下高频信息,因为一般高频能量比低频小。其预加重函数如下所示:
y ( n ) = x ( n ) − α ⋅ x ( n − 1 ) y(n)=x(n)-\alpha \cdot x(n-1) y(n)=x(n)−α⋅x(n−1)
其中 α \alpha α一般取值为 0.97 、 0.95 0.97、0.95 0.97、0.95
%预加重y=x(i)-0.97*x(i-1)
for i=2:200000
y(i)=x(i)-0.97*x(i-1);
end
y=y';%对y取转置
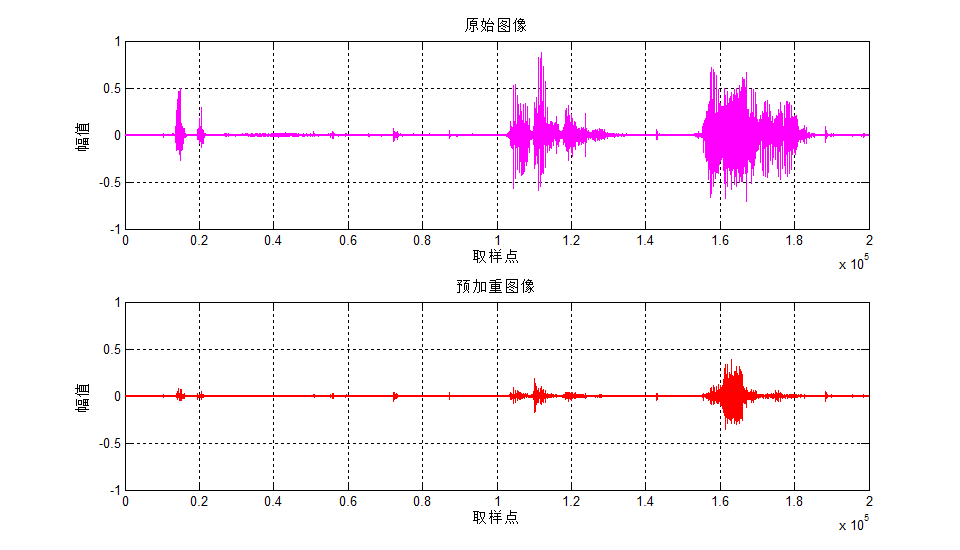
然后我们再来对比一下原始文件和预加重后的数据差异
我们可以看到整个的数据其幅度范围是有所减小的,但是可以看得出来,高频部分的缩小倍数是小于低频部分的缩小倍数的。
3.3 分帧{S(301*1103)}
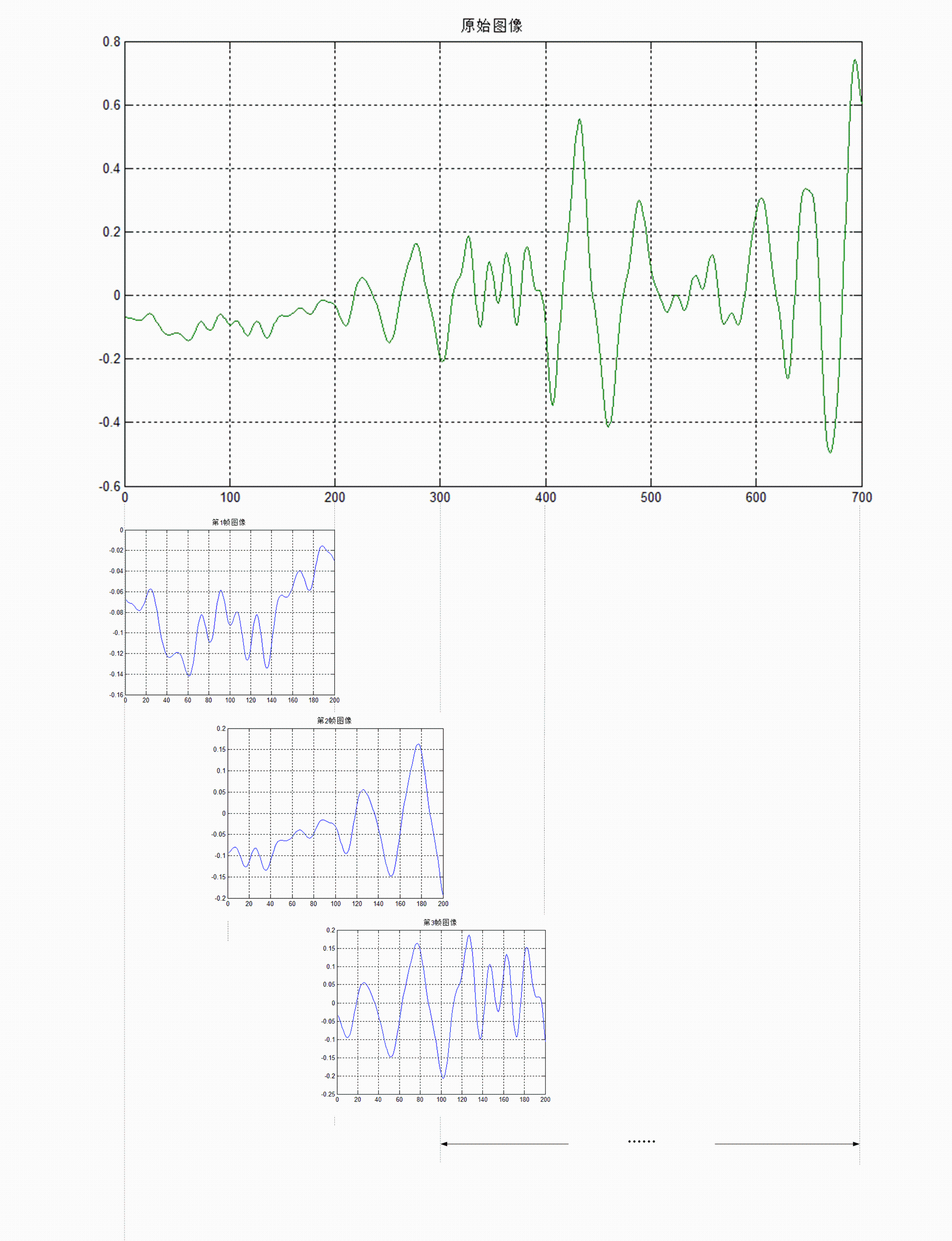
\qquad 我们要对语音数据做傅里叶变换,将信息从时域转化为频域。但是如果对整段语音做FFT,就会损失时序信息。因此,我们假设在很短的一段时间t内的频率信息不变,对长度为t的帧做傅里叶变换,就能得到对语音数据的频域和时域信息的适当表达。例如我们这里的采样点数为200000个点,如果真的这样做的话,就很麻烦了,于是我们在语音分析中引入分帧的概念,将原始语音信号分成大小固定的N段语音信号,这里每一段语音信号都被称为一帧。
\qquad 但是,如果我们这样分帧的话,帧与帧之间的连贯性就会变差,于是我们每一帧的前N个采样点数据与前一帧的后N个采样点数据一样。其原理图大致如下所示:
\qquad 对于整个采样点数据可以分为多少帧以及帧与帧之间交叉的采样点个数N,不是随便分的,一般来说帧长设置为 25 m s 25ms 25ms,帧移设置为 10 m s 10ms 10ms,对于我这次的仿真,其帧数和帧长数值如下:
帧数 = f s ⋅ 0.025 = 44100 ⋅ 0.025 = 1103 ( 个采样点 ) 帧移 = f s ⋅ 0.001 = 44100 ⋅ 0.01 = 441 ( 个采样点 ) \quad 帧数=f_s \cdot 0.025=44100 \cdot0.025=1103(个采样点)\\ \quad \\ \quad 帧移=f_s \cdot 0.001=44100 \cdot 0.01=441(个采样点) 帧数=fs⋅0.025=44100⋅0.025=1103(个采样点)帧移=fs⋅0.001=44100⋅0.01=441(个采样点)
\qquad 在这里我们要调用matlab的enframe函数来进行分帧操作,要知道这个函数是包含在voicebox工具箱里边,首先确保其已经安装成功。
S=enframe(y,1103,662);%分帧,对y进行分帧,x为没有预加重的语音序列
%每帧长度为1103个采样点,每帧之间非重叠部分为662个采样点
%1103=44100*0.025, 441=44100*0.01 662=1103-441
%根据计算,我们可以将108721个数据根据公式662*301+1103=200365
%可以将其分为301帧
3.4 加窗{C(301*1103)}
\qquad 将信号分帧后,我们将每一帧代入窗函数,窗外的值设定为0,其目的是消除各个帧两端可能会造成的信号不连续性(即谱泄露 spectral leakage)。常用的窗函数有方窗、汉明窗和汉宁窗等,根据窗函数的频域特性,常采用汉明窗(hamming window)。接下来我来讲解一下怎么加窗:我们需要做的就是为每一帧数据,也就是301帧数据都加入大小为1103的汉明窗。其汉明窗的表达公式如下所示:
W ( n ) = ( 1 − a ) − a ⋅ c o s ( 2 ⋅ π ⋅ n / N ) 1 ≤ n ≤ N W(n)=(1-a)-a \cdot cos(2\cdot \pi \cdot n/N) \qquad 1 \leq n \leq N W(n)=(1−a)−a⋅cos(2⋅π⋅n/N)1≤n≤N
对于a的取值不同,将会产生不同的汉明窗,一般情况下, a = 0.46 a=0.46 a=0.46
%尝试一下汉明窗a=0.46,得到汉明窗W=(1-a)-a*cos(2*pi*n/N)
n=1:1103;
W=0.54-0.46*cos((2*pi.*n)/1103)
plot(W);title('汉明窗');grid on;
xlabel('取样点');ylabel('幅值')
%创建汉明窗矩阵C
C=zeros(301,1103);
for i=1:301
C(i,:)=W;
end
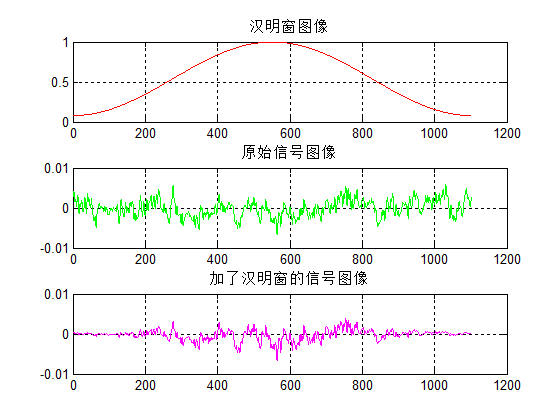
\qquad 由上边的公式我们可以得到汉明窗矩阵 C ( 301 , 1103 ) C_{(301,1103)} C(301,1103),其矩阵大小为(301,1103),由于汉明窗矩阵和分帧后的矩阵S具有相同大小,所以在matlab中使这两个矩阵的对应位置相乘,即可得到加窗后的矩阵 S C ( 301 , 1103 ) SC_{(301,1103)} SC(301,1103),其大小为(301,1103)。接下来我将随便选取一帧数据来展示一下汉明窗、原始数据、加窗后的数据。其matlab代码如下所示:
SC=S.*C;
subplot(3,1,1);plot(C(7,:),'r');
title('汉明窗图像');grid on;%画出第7帧的汉明窗图像
subplot(3,1,2);plot(S(7,:),'g');
title('原始信号图像');grid on;%画出第7帧的原始信号图像
subplot(3,1,3);plot(SC(7,:),'m');
title('加了汉明窗的信号图像');grid on;%画出第7帧加了汉明窗的信号图像
\qquad 在上边的图示中我们就可以看到,在每一帧的低频部分和高频部分都被汉明窗相乘后起了较大抑制作用,使其结果接近于0。
3.5 傅里叶变换
\qquad 对于加窗后的矩阵 S C ( 301 , 1103 ) SC_{(301,1103)} SC(301,1103),它是一个301*1103的矩阵,也就是说,它有301帧数据,且每一帧数据都有1103个采样点,那么我们接下来就要对这301帧的每一帧都要进行N=4096的FFT快速傅里叶变换,得到一个大小为(301,4096)大小的矩阵 D ( 301 , 4096 ) D_{(301,4096)} D(301,4096),其帧数还是301帧,对每一帧的4096个数据点分别取模再取平方,然后除以4096;便得到能量谱密度 E ( 301 , 4096 ) E_{(301,4096)} E(301,4096),其大小为301×4096,然后再对每一帧得到的能量进行相加,即得到一个301×1的矩阵 F ( 301 , 1 ) F_{(301,1)} F(301,1),其中的每个元素代表每一帧能量的总和。
%对SC的每一帧都进行N=4096的快速傅里叶变换,得到一个301*4096的矩阵
F=0;N=4096;
for i=1:301
%对SC作N=4096的FFT变换
D(i,:)=fft(SC(i,:),N);
%以下循环实现求取能量谱密度E
for j=1:N
t=abs(D(i,j));
E(i,j)=(t^2)/N;
end
%获取每一帧的能量总和F(i)
F(i)=sum(D(i,:));
end
3.6 梅尔滤波器
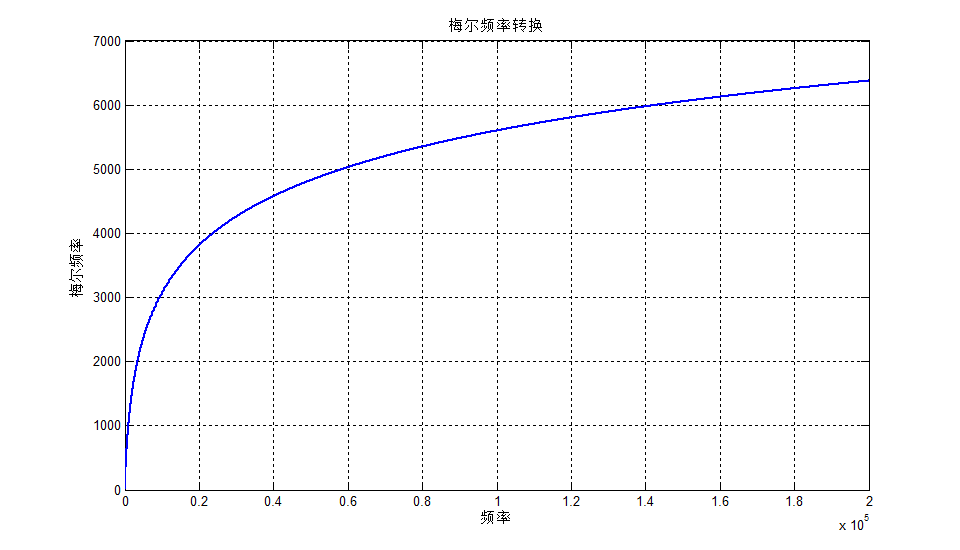
\qquad 首先我要讲一下什么是梅尔值,这是一个新的量度,相比于正常的频率机制,梅尔值更加接近于人耳的听觉机制,其在低频范围内增长速度很快,但在高频范围内,梅尔值的增长速度很慢。每一个频率值都对应着一个梅尔值,其对应关系如下
m = 2595 ⋅ l o g 10 ( 1 + f 700 ) m=2595 \cdot log_{10}(1+\frac{f}{700}) m=2595⋅log10(1+700f)
在matlab上画出其对应图像如下所示:
对于该函数图像的显示的matlab代码如下所示:
%梅尔频率转化函数图像
for i=1:200000
mel(i)=2595*log10(1+i/700);
end
set(gcf,'position',[180,160,960,550]);%设置画图的大小
plot(mel,'linewidth',1.5);grid on;
title('梅尔频率转换');xlabel('频率');ylabel('梅尔频率');
但是如果我们要将梅尔频率m转换为频率f呢,我们对上式整理即可得到:
f = 700 ⋅ ( 1 0 m / 2595 − 1 ) f=700 \cdot (10^{m/2595}-1) f=700⋅(10m/2595−1)
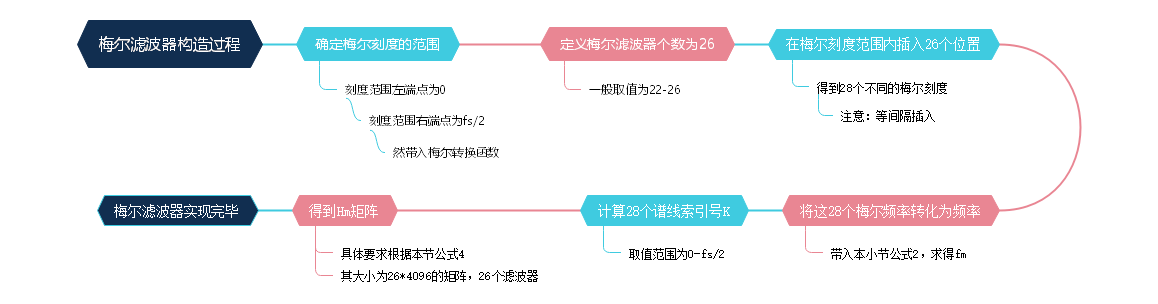
\qquad 好了介绍到这里,对于如何得到梅尔滤波器组我们还是无从下手,于是,我在这里描述了一下获得梅尔滤波器的几个简单步骤。然后接下来的操作我们也就将会按照这个步骤来实现。
fl=0;fh=fs/2;%定义频率范围,低频和高频
bl=2595*log10(1+fl/700);%得到梅尔刻度的最小值
bh=2595*log10(1+fh/700);%得到梅尔刻度的最大值
%梅尔坐标范围
p=26;%滤波器个数
B=bh-bl;%梅尔刻度长度
mm=linspace(0,B,p+2);%规划28个不同的梅尔刻度
fm=700*(10.^(mm/2595)-1);%将Mel频率转换为频率
上边几步都比较好理解,但是对于接下来谱线索引号k的定义,或许就需要一些理解了,其定义公式如下所示:
k = ( 1 + N ) ⋅ f m f s k=\frac{(1+N)\cdot f_m}{f_s} k=fs(1+N)⋅fm
\qquad 其中 N N N为FFT点数, f s f_s fs为抽样频率, f m f_m fm为之前那28个梅尔刻度转化为频率后的值,最后我们得到的 k k k值为一个1*28的矩阵。且k值范围为 0 − N / 2 0-N/2 0−N/2。这个式子是把频率对应到频谱中2048个频率分量的某个。
以下则是k值得求解过程:
k=((N+1)*fm)/fs%计算28个不同的k值
hm=zeros(26,N);%创建hm矩阵
df=fs/N;
freq=(0:N-1)*df;%采样频率值
好了,现在我们只剩下最后一步了,创建Hm矩阵,这个矩阵得定义如下所示:
H m ( k ) = { 0 k < f ( m − 1 ) 2 ( k − f ( m − 1 ) ) ( f ( m + 1 ) − f ( m − 1 ) ) ( f ( m ) − f ( m − 1 ) ) f ( m − 1 ) ≤ k ≤ f ( m ) 2 ( f ( m + 1 ) − k ) ( f ( m + 1 ) − f ( m − 1 ) ) ( f ( m ) − f ( m − 1 ) ) f ( m ) ≤ k ≤ f ( m + 1 ) 0 k ≥ f ( m + 1 ) H_m(k)=\begin{cases} 0& \text{k}<f(m-1)\\ \frac{2(k-f(m-1))}{(f(m+1)-f(m-1))(f(m)-f(m-1))}& f(m-1)\le k \le f(m)\\ \frac{2(f(m+1)-k)}{(f(m+1)-f(m-1))(f(m)-f(m-1))}& f(m)\le k \le f(m+1)\\ 0& k\ge f(m+1) \end{cases} Hm(k)=⎩
⎨
⎧0(f(m+1)−f(m−1))(f(m)−f(m−1))2(k−f(m−1))(f(m+1)−f(m−1))(f(m)−f(m−1))2(f(m+1)−k)0k<f(m−1)f(m−1)≤k≤f(m)f(m)≤k≤f(m+1)k≥f(m+1)
\qquad 上式中的m代表第几个滤波器,k为横坐标0-2048。26个滤波器就是算2049个频率分量分别属于26个频率带的概率.根据上式计算26个滤波器的二维数组,也就是26*4096二维数组Hm.
以下贴出步骤6 Hm矩阵的求解
for i=2:27
%取整,这里取得是28个k中的第2-27个,舍弃0和28
n0=floor(k(i-1));
n1=floor(k(i));
n2=floor(k(i+1));
%要知道k(i)分别代表的是每个梅尔值在新的范围内的映射,其取值范围为:0-N/2
%以下实现公式--,求取三角滤波器的频率响应。
for j=1:N
if n0<=j & j<=n1
hm(i-1,j)=2*(j-n0)/((n2-n0)*(n1-n0));
elseif n1<=j & j<=n2
hm(i-1,j)=2*(n2-j)/((n2-n0)*(n1-n0));
end
end
%此处求取H1(k)结束。
end
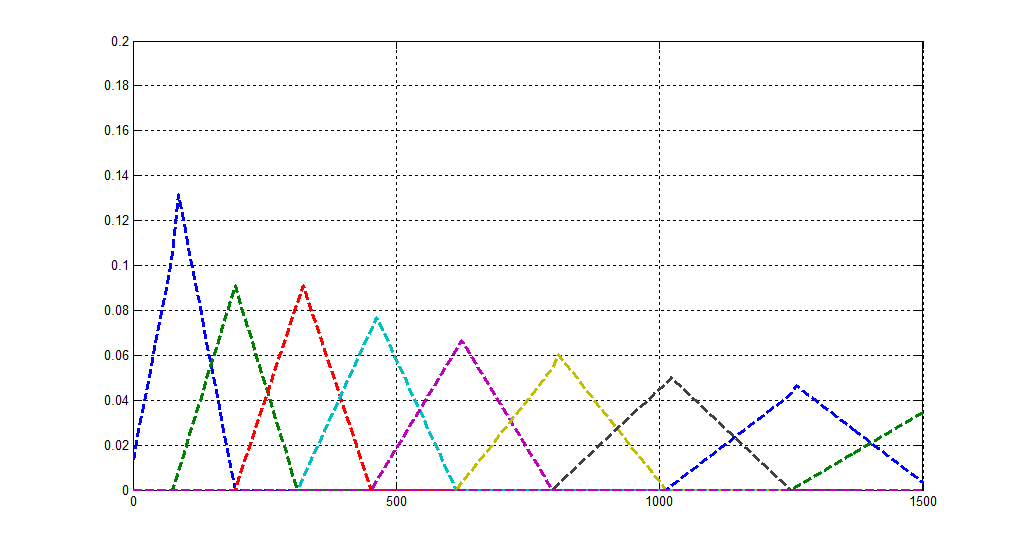
接下来将要进行最后一步,输出Hm矩阵,并且将梅尔滤波器组画出来。
%绘图,且每条颜色显示不一样
c=colormap(lines(26));%定义26条不同颜色的线条
set(gcf,'position',[180,160,1020,550]);%设置画图的大小
for i=1:26
plot(freq,hm(i,:),'--','color',c(i,:),'linewidth',2.5);%开始循环绘制每个梅尔滤波器
hold on
end
grid on;%显示方格
axis([0 1500 0 0.2]);%设置显示范围
\qquad 画出来之后,我们就会发现该梅尔滤波器,在频率很小的时候,滤波器宽度很窄,随着其频率的增大,滤波器的宽度也会逐渐增大,但其幅值也会逐渐减小。
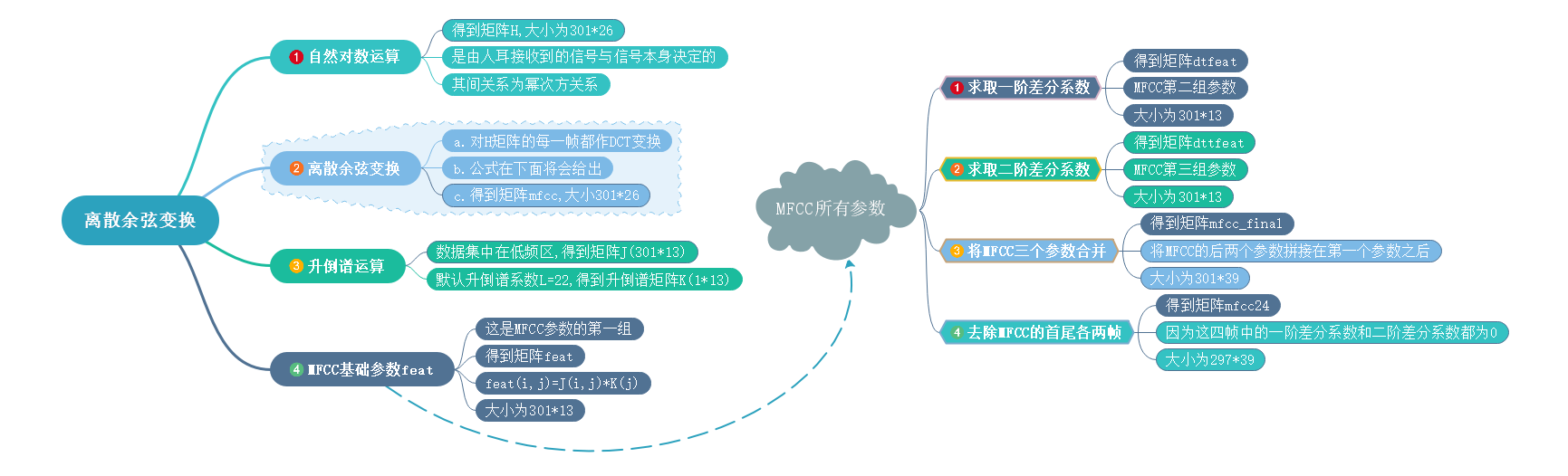
3.7 离散余弦变换
\qquad 在进行离散余弦变换之前,我们还需要做的就是把第3.5节得到的二维矩阵能量谱 E ( 301 , 4096 ) E_{(301,4096)} E(301,4096),乘以第3.6节得到的二维数组梅尔滤波器 H m ( 26 ∗ 4096 ) Hm_{(26*4096)} Hm(26∗4096)的转置,矩阵的转置可得到301*26的矩阵,然后满足矩阵乘法定律,得到参数H,其定义如下:
H = E ⋅ H m T H=E \cdot H_m^T H=E⋅HmT
此处的H其实是301×26的二维矩阵。
\qquad 由于滤波器组得到的系数是相关性很高的,因此我们用离散余弦变换(Discrete Cosine Transform)来去相关并且降维。一般来说,在自动语音识别(Automatic Speech Recognition)领域,因为大部分信号数据一般集中在变换后的低频区,所以对每一帧只取前13个数据就好了。
好了接下来我们就要进行离散余弦变换了,但是在开始之前我感觉还是先讲解一下其具体的步骤流程吧。
根据mfcc的定义,我们需要对能量的对数作离散余弦变换,即可得到MFCC参数:
m f c c ( i , n ) = ∑ m = 1 M l o g [ H ( i , m ) ] ⋅ c o s [ π ⋅ n ⋅ ( 2 m − 1 ) 2 M ] mfcc(i,n)=\sum_{m=1}^{M}log[H(i,m)] \cdot cos[\frac{\pi \cdot n \cdot(2m-1)}{2M}] mfcc(i,n)=m=1∑Mlog[H(i,m)]⋅cos[2Mπ⋅n⋅(2m−1)]
\qquad 其中H为我们上边得到的矩阵H,M代表梅尔滤波器个数,i代表第几帧数据(取值为1-301),n代表第i帧的第n列(n取值范围为1-26)。那么根据上述公式我们可以写出求取mfcc的代码如下:
H=E*hm';
%对H作自然对数运算
%因为人耳听到的声音与信号本身的大小是幂次方关系,所以要求个对数
for i=1:301
for j=1:26
H(i,j)=log(H(i,j));%取对数运算
end
end
%作离散余弦变换
for i=1:301
for j=1:26
%先求取每一帧的能量总和
sum=0;
%作离散余弦变换
for p=1:26
sum=sum+H(i,p)*cos((pi*j)*(2*p-1)/(2*26));
end
mfcc(i,j)=((2/26)^0.5)*sum;
%完成离散余弦变换
end
end
\qquad 接下来我们就要根据公式进行升倒谱的计算了,前边我们已经讲到了,因为大部分的信号数据一般集中在变换后的低频区,所以对每一帧只取前13个数据就好了。其公式表达如下:
K ( i ) = 1 + ( L 2 ) ⋅ s i n ( π ⋅ i L ) i = 1 , 2 , 3… , 13 K(i)=1+(\frac{L}{2})\cdot sin(\frac{\pi \cdot i}{L}) \qquad i=1,2,3…,13 K(i)=1+(2L)⋅sin(Lπ⋅i)i=1,2,3…,13
\qquad 其中L为升倒谱系数,一般取值为22,我们将其带入即可求得矩阵K,这是一个1×13大小的矩阵,这一部分的升倒谱的其实现代码如下:
J=mfcc(:,(1:13));
%默认升到普系数为22
for i=1:13
K(i)=1+(22/2)*sin(pi*i/22);
end
接下来我们就要求取MFCC的三个参数了,首先我们先获取mfcc的第一组数据,根据公式:
f e a t ( i , j ) = J ( i , j ) ⋅ K ( j ) i = 1 , 2 , 3 , . . . , 301 ; j = 1 , 2 , . . . , 13 feat(i,j)=J(i,j) \cdot K(j)\\ \quad \\ \quad i=1,2,3,…,301; \quad j=1,2,…,13 feat(i,j)=J(i,j)⋅K(j)i=1,2,3,…,301;j=1,2,…,13
根据公式我们可以实现如下代码:
%得到二维数组feat,这是mfcc的第一组数据,默认为三组
for i=1:301
for j=1:13
L(i,j)=J(i,j)*K(j);
end
end
feat=L;%将其值赋值到feat矩阵
\qquad 接下来就是求取MFCC的第二组,第三组参数了。第二组参数其实就是在已有的基础参数下作一阶微分操作,第三组参数在第二组参数下作一阶微分操作。那么表达公式事什么样的呢,别急,等我慢慢道来:
d t f e a t [ i ] [ j ] = f e a t [ i + 1 ] [ j ] − f e a t [ i − 1 ] [ j ] + 2 ⋅ f e a t [ i + 2 ] [ j ] − 2 ⋅ f e a t [ i − 2 ] [ j ] i = 1 , 2 , 3 , . . . , 301 ; j = 1 , 2 , 3… , 13 dtfeat[i][j]=feat[i+1][j]-feat[i-1][j]+2\cdot feat[i+2][j]-2 \cdot feat[i-2][j] \\ \quad \\ i=1,2,3,…,301 \quad; \quad j=1,2,3…,13 dtfeat[i][j]=feat[i+1][j]−feat[i−1][j]+2⋅feat[i+2][j]−2⋅feat[i−2][j]i=1,2,3,…,301;j=1,2,3…,13
按照上边的公式,我们可以使用代码实现一阶求导和二阶求导的计算
%接下来求取第二组(一阶差分系数)301x13 ,这也是mfcc参数的第二组参数
dtfeat=0;
dtfeat=zeros(size(L));%默认初始化
for i=3:299
dtfeat(i,:)=-2*feat(i-2,:)-feat(i-1,:)+feat(i+1,:)+2*feat(i+2,:);
end
dtfeat=dtfeat/10;
%求取二阶差分系数,mfcc参数的第三组参数
%二阶差分系数就是对前面产生的一阶差分系数dtfeat再次进行操作。
dttfeat=0;
dttfeat=zeros(size(dtfeat));%默认初始化
for i=3:299
dttfeat(i,:)=-2*dtfeat(i-2,:)-dtfeat(i-1,:)+dtfeat(i+1,:)+2*dtfeat(i+2,:);
end
dttfeat=dttfeat/10;
%这里的10是根据数据确定的
\qquad 好了到这里我们就完成了,MFCC三组参数的求解,我们现在就只需要将这三组数据拼接到一起形成一个301×39的矩阵即可。其实现代码如下:
%将得到的mfcc的三个参数feat、dtfeat、dttfeat拼接到一起
%得到最后的mfcc系数301x39
mfcc_final=0;
mfcc_final=[feat,dtfeat,dttfeat];%拼接完成
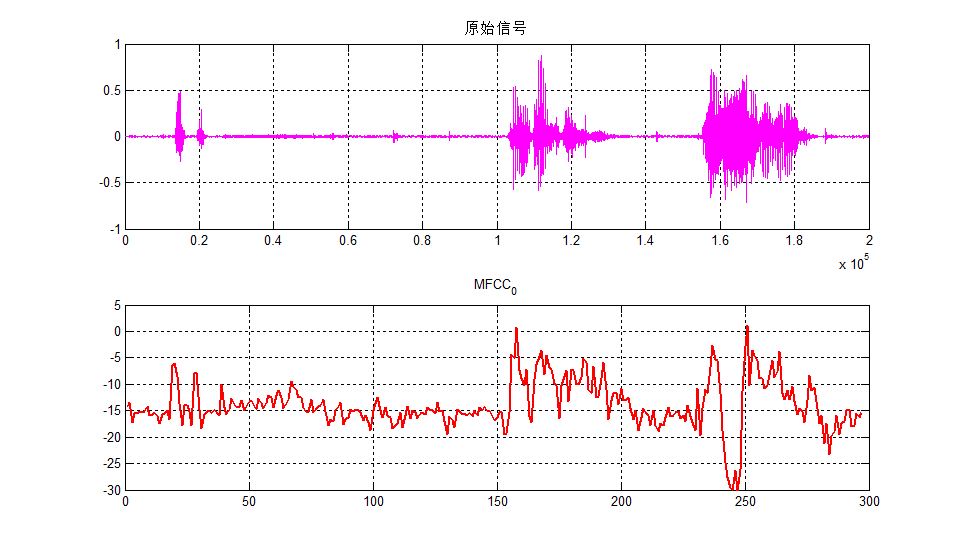
\qquad 前面导图中,我们也有讲到过,由于一阶求导和二阶求导的前两帧和后两帧数据都为0,于是我们就要对在mfcc_final中去除这四帧数据。而后我们再选取每一帧的mfcc系数的第一个数得到 M F C C 0 MFCC_0 MFCC0,这是一个297×1的数据,对 M F C C 0 MFCC_0 MFCC0来进行绘图,并与原始信号进行比对。
mfcc24=mfcc_final((3:299),:);
%以下画图对比一下原始信号和提取出来的mfcc0
set(gcf,'position',[180,160,960,550]);%设置画图的大小
subplot(211)
plot(x,'m');grid on;
title('原始信号');
axis([0 200000 -1 1]);%对数据,进行绘图
mfcc0=mfcc24(:,1)%选取mfcc系数的第一个数,组成新的特征参数mfcc0
subplot(212)
mfcc00=(mfcc0-80)/2 %PS:这里不在mfcc求取过程步骤中,我只是为方便作图而修改的这里,希望大家可以理解。MFCC参数的求取过程并无此操作
plot(mfcc00,'r','linewidth',2);
title('MFCC_0');
axis([0 300 -30 5]);grid on
比对结果如下所示:
\qquad 好了,到了这里我们就可以看到了,原始信号之前是20000个采样点的数据,而现在的 M F C C 0 MFCC_0 MFCC0参数图形大致与原始信号一致,并且其点数只有297个点,这也就说明通过此方法 M F C C 0 MFCC_0 MFCC0,我们可以提取出语音信号的特点以及走向趋势,也就是说在某个程度上我们可以用这297个点来代替 2 ⋅ 1 0 5 2 \cdot 10^5 2⋅105点的数据。
3.8 注(2022年5月3日修)
上边图示 M F C C 0 MFCC_0 MFCC0仅为语音MFCC参数的第一维参数,因其( M F C C 0 MFCC_0 MFCC0)包含了语音信号的时域能量信息,所以一般被用来用作语音信号的 端点检测。另外还有很多同学对变量的理解不是那么明白,这里特此说明一下:
| 实验中变量 | 描述 |
|---|---|
| feat | MFCC参数 |
| dtfeat | MFCC参数的一阶差分 |
| dttfeat | MFCC参数的二阶差分 |
| mfcc_final | MFCC参数+一阶差分+二阶差分 |
| M F C C 0 MFCC_0 MFCC0 | MFCC参数的第一维参数 |
最后还是要说明一下,此篇博客只是为了让大家深入理解MFCC特征的求取过程,所以其在 运行速度 和 代码规范性 方面未作过多优化,如果大家是用于做实验研究,建议大家可以直接调用matlab自带的mfcc函数(matlab2019版以后已经自带mfcc的函数),
[x,fs]=audioread(filename);%读取wav文件
wlen=512;%帧长
inc=256;%帧移
dim=13;%MFCC参数维度
[mfccs,delta_mfcc,delta_delta_mfcc]= mfcc(x,fs,'WindowLength',wlen,'OverlapLength',inc ,'NumCoeffs',dim,'LogEnergy','Ignore');
%%这里mfccs表示13维的mfcc参数,delta_mfcc表示其一阶差分,delta_delta_mfcc表示其二阶差分
那如果你的matlab版本较低,则可以参考4.1节代码。
4.总结
本次训练是在参考了很多资料的前提下完成的,为了防止自己忘记,所以特此写了本篇文章。
4.1更新(2021.5.9)
很多同学想要这个mfcc版本的完整版,再加之上边的讲解是只针对自己语音,一些语音长度,包括语音帧数使得部分同学难以理解,所以在这里我又将程序进行了一下修改,使同学们可以自己输入自己的音频文件,并返回mfccs参数矩阵:
function [mfcc_final]=Mymfcc(filename)
frameSize=512;
inc=160;
[x,fs]=audioread(filename);%读取wav文件
N=length(x);
%预加重y=x(i)-0.97*x(i-1)
for i=2:N
y(i)=x(i)-0.97*x(i-1);
end
y=y';%对y取转置
S=enframe(y,frameSize,inc);%分帧,对x进行分帧,
[a b]=size(S);
%尝试一下汉明窗a=0.46,得到汉明窗W=(1-a)-a*cos(2*pi*n/N)
n=1:b;
W=0.54-0.46*cos((2*pi.*n)/b);
%创建汉明窗矩阵C
C=zeros(a,b);
ham=hamming(b);
for i=1:a
C(i,:)=ham;
end
%将汉明窗C和S相乘得SC
SC=S.*C;
F=0;N=4096;
for i=1:a
%对SC作N=4096的FFT变换
D(i,:)=fft(SC(i,:),N);
%以下循环实现求取能量谱密度E
for j=1:N
t=abs(D(i,j));
E(i,j)=(t^2)/N;
end
%获取每一帧的能量总和F(i)
F(i)=sum(D(i,:));
end
%将频率转换为梅尔频率
%梅尔频率转化函数图像
N1=length(x)
for i=1:N1
mel(i)=2595*log10(1+i/700);
end
fl=0;fh=fs/2;%定义频率范围,低频和高频
bl=2595*log10(1+fl/700);%得到梅尔刻度的最小值
bh=2595*log10(1+fh/700);%得到梅尔刻度的最大值
%梅尔坐标范围
p=26;%滤波器个数
B=bh-bl;%梅尔刻度长度
mm=linspace(0,B,p+2);%规划28个不同的梅尔刻度
fm=700*(10.^(mm/2595)-1);%将Mel频率转换为频率
W2=N/2+1;%fs/2内对应的FFT点数,2049个频率分量
k=((N+1)*fm)/fs%计算28个不同的k值
hm=zeros(26,N);%创建hm矩阵
df=fs/N;
freq=(0:N-1)*df;%采样频率值
%绘制梅尔滤波器
for i=2:27
%取整,这里取得是28个k中的第2-27个,舍弃0和28
n0=floor(k(i-1));
n1=floor(k(i));
n2=floor(k(i+1));
%要知道k(i)分别代表的是每个梅尔值在新的范围内的映射,其取值范围为:0-N/2
%以下实现公式--,求取三角滤波器的频率响应。
for j=1:N
if n0<=j & j<=n1
hm(i-1,j)=2*(j-n0)/((n2-n0)*(n1-n0));
elseif n1<=j & j<=n2
hm(i-1,j)=2*(n2-j)/((n2-n0)*(n1-n0));
end
end
%此处求取H1(k)结束。
end
%绘图,且每条颜色显示不一样
c=colormap(lines(26));%定义26条不同颜色的线条
figure(1)
set(gcf,'position',[180,160,1020,550]);%设置画图的大小
for i=1:26
plot(freq,hm(i,:),'--','color',c(i,:),'linewidth',2.5);%开始循环绘制每个梅尔滤波器
hold on
end
grid on;%显示方格
axis([0 1500 0 0.1]);%设置显示范围
%得到能量特征参数的和
H=E*hm';
%对H作自然对数运算
%因为人耳听到的声音与信号本身的大小是幂次方关系,所以要求个对数
for i=1:a
for j=1:26
H(i,j)=log(H(i,j));
end
end
%作离散余弦变换 具体参考信号检测与估计的论文
for i=1:a
for j=1:26
%先求取每一帧的能量总和
sum1=0;
%作离散余弦变换
for p=1:26
sum1=sum1+H(i,p)*cos((pi*j)*(2*p-1)/(2*26));
end
mfcc(i,j)=((2/26)^0.5)*sum1;
%完成离散余弦变换
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%% 以下为求取mfcc的三个参数过程 %%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%作升倒谱运算
%因为大部分的信号数据一般集中在变换后的低频区,所以对每一帧只取前13个数据就好了
J=mfcc(:,(1:13));
%默认升到普系数为22
for i=1:13
K(i)=1+(22/2)*sin(pi*i/22);
end
%得到二维数组feat,这是mfcc的第一组数据,默认为三组
for i=1:a
for j=1:13
L(i,j)=J(i,j)*K(j);
end
end
feat=L;
%接下来求取第二组(一阶差分系数)301x13 ,这也是mfcc参数的第二组参数
dtfeat=0;
dtfeat=zeros(size(L));%默认初始化
for i=3:a-2
dtfeat(i,:)=-2*feat(i-2,:)-feat(i-1,:)+feat(i+1,:)+2*feat(i+2,:);
end
dtfeat=dtfeat/10;%这里的/10,是我自己在实现过程中的操作,原mfcc的差分求取并无/10操作(2022年5月3日注)
%求取二阶差分系数,mfcc参数的第三组参数
%二阶差分系数就是对前面产生的一阶差分系数dtfeat再次进行操作。
dttfeat=0;
dttfeat=zeros(size(dtfeat));%默认初始化
for i=3:a-2
dttfeat(i,:)=-2*dtfeat(i-2,:)-dtfeat(i-1,:)+dtfeat(i+1,:)+2*dtfeat(i+2,:);
end
dttfeat=dttfeat/10;%同上dtfeat
%这里的10是根据数据确定的,默认为2
%将得到的mfcc的三个参数feat、dtfeat、dttfeat拼接到一起
%得到最后的mfcc系数301x39
mfcc_final=0;
mfcc_final=[feat,dtfeat,dttfeat];%拼接完成
上边封装的函数是我根据上边分步讲解的内容,封装为Mymfcc函数,调用方法也很简单:
mfccs=Mymfcc('bluesky1.wav')
这里返回的参数就是一个197*39的mfcc参数矩阵,当然这个矩阵的大小还是由输入的语音长度决定的。
4.2.实验中diguashao.wav自取(2022年5月3日更新)
实验过程中,有些同学如果想要实验过程中的 diguashao.wav,我已经将该文件上传至百度网盘地址链接,提取码为:fjq6
希望可以帮助到大家。
5.参考文献,资料
1.基于谱熵梅尔积的语音端点检测方法
2.语音识别MFCC
3.语音特征参数MFCC提取过程详解
4.Mel滤波器组的设计与实现(基于MATLAB和Python)
今天的文章mfcc算法 实现_matlab输出数值取消科学计数法分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/74294.html