分治算法-大整数乘法

大整数乘法：就是乘法的两个乘数比较大，最后结果超过了整型甚至长整型的最大范围，此时如果需要得到精确结果，就不能常规的使用乘号直接计算了。没错，就需要采用分治的思想，将乘数“分割”，将大整数计算转换为小整数计算。

可以通过列表的形式来进行大整数的乘法，通过数组来保存列表中的数据。结合http://blog.csdn.net/tjsinor2008/article/details/5625849

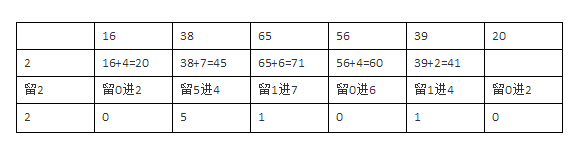
计算8765*234的结果：
（1）

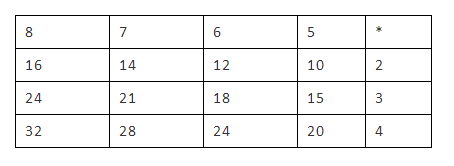
（2）

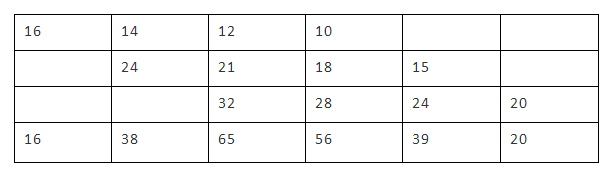
（3）

最后算出的结果即为2051010。
根据以上思路就可以编写C程序了，再经分析可得：

1，一个m位的整数与一个n位的整数相乘，乘积为m+n-1位或m+n位。

2，程序中，用三个字符数组分别存储乘数，被乘数与乘积。由第1点分析知，存放乘积的字符数组饿长度应不小于存放乘数与被乘数的两个数组的长度之和。

3，可以把第二步“计算填表”与第三四步“累加进位”放在一起完成，可以节省存储表格2所需的空间。

4，程序关键部分是两层循环，内层循环累计一数组的和，外层循环处理保留的数字和进位。

效率的提升：
当然在计算生成这个二维表时，不必一位一位的乘，而可以三位三位的乘；在累加时也是满1000进位。这样，我们计算m位整数乘以n位整数，只需要进行m*n/9次乘法运算，再进行约（m+n）/3次加法运算和（m+n）/3次去摸运算。总体看来，效率是前一种算法的9倍。
有人可能会想：既然能用三位三位的乘，为什么不能4位4位的乘，甚至5位。听我解来：本算法在累加表中斜线间的数字时，如果用无符号长整数（范围0至~4294967295）作为累加变量，在最不利的情况下（两个乘数的所有数字均为9），能够累加约4294967295/（999*999）=4300次，也就是能够准确计算任意两个约不超过12900（每次累加的结果“值”三位，故4300*3=12900）位的整数相乘。如果4位4位地乘，在最不利的情况下，能过累加月4294967295/(9999*9999)=43次，仅能够确保任意两个不超过172位的整数相乘，没什么实用价值，更不要说5位了。

下面用Java实现该算法。

package com.example;
import java.util.Scanner;
import java.util.regex.Matcher;
import java.util.regex.Pattern;


/** * 大整数乘法 * @author * */
public class 大整数乘法 { 
   

    //规模只要在这个范围内就可以直接计算了
    private final static int SIZE = 4;

    // 此方法要保证入参len为X、Y的长度最大值
    private static String bigIntMultiply(String X, String Y, int len)
    {
        // 最终返回结果
        String str = "";
        // 补齐X、Y，使之长度相同
        X = formatNumber(X, len);
        Y = formatNumber(Y, len);

        // 少于4位数，可直接计算
        if (len <= SIZE)
        {
            return "" + (Integer.parseInt(X) * Integer.parseInt(Y));
        }

        // 将X、Y分别对半分成两部分
        int len1 = len / 2;
        int len2 = len - len1;
        String A = X.substring(0, len1);
        String B = X.substring(len1);
        String C = Y.substring(0, len1);
        String D = Y.substring(len1);

        // 乘法法则，分块处理
        int lenM = Math.max(len1, len2);
        String AC = bigIntMultiply(A, C, len1);
        String AD = bigIntMultiply(A, D, lenM);
        String BC = bigIntMultiply(B, C, lenM);
        String BD = bigIntMultiply(B, D, len2);

        // 处理BD，得到原位及进位
        String[] sBD = dealString(BD, len2);

        // 处理AD+BC的和
        String ADBC = addition(AD, BC);
        // 加上BD的进位
        if (!"0".equals(sBD[1]))
        {
            ADBC = addition(ADBC, sBD[1]);
        }

        // 得到ADBC的进位
        String[] sADBC = dealString(ADBC, lenM);

        // AC加上ADBC的进位
        AC = addition(AC, sADBC[1]);

        // 最终结果
        str = AC + sADBC[0] + sBD[0];

        return str;
    }

    // 两个数字串按位加
    private static String addition(String ad, String bc)
    {
        // 返回的结果
        String str = "";

        // 两字符串长度要相同
        int lenM = Math.max(ad.length(), bc.length());
        ad = formatNumber(ad, lenM);
        bc = formatNumber(bc, lenM);

        // 按位加，进位存储在temp中
        int flag = 0;

        // 从后往前按位求和
        for (int i = lenM - 1; i >= 0; i--)
        {
            int t =
                flag + Integer.parseInt(ad.substring(i, i + 1))
                    + Integer.parseInt(bc.substring(i, i + 1));

            // 如果结果超过9，则进位当前位只保留个位数
            if (t > 9)
            {
                flag = 1;
                t = t - 10;
            }
            else
            {
                flag = 0;
            }

            // 拼接结果字符串
            str = "" + t + str;
        }
        if (flag != 0)
        {
            str = "" + flag + str;
        }
        return str;
    }

    // 处理数字串，分离出进位；
    // String数组第一个为原位数字，第二个为进位
    private static String[] dealString(String ac, int len1)
    {
        String[] str = {ac, "0"};
        if (len1 < ac.length())
        {
            int t = ac.length() - len1;
            str[0] = ac.substring(t);
            str[1] = ac.substring(0, t);
        }
        else
        {
            // 要保证结果的length与入参的len一致，少于则高位补0
            String result = str[0];
            for (int i = result.length(); i < len1; i++)
            {
                result = "0" + result;
            }
            str[0] = result;
        }
        return str;
    }

    // 乘数、被乘数位数对齐
    private static String formatNumber(String x, int len)
    {
        while (len > x.length())
        {
            x = "0" + x;
        }
        return x;
    }

    //测试桩
    public static void main(String[] args)
    {
        // 正则表达式：不以0开头的数字串
        String pat = "^[1-9]\\d*$";
        Pattern p = Pattern.compile(pat);

        // 获得乘数A
        System.out.println("请输入乘数A（不以0开头的正整数）：");
        Scanner sc = new Scanner(System.in);
        String A = sc.nextLine();
        Matcher m = p.matcher(A);
        if (!m.matches())
        {
            System.out.println("数字不合法！");
            return;
        }

        // 获得乘数B
        System.out.println("请输入乘数B（不以0开头的正整数）：");
        sc = new Scanner(System.in);
        String B = sc.nextLine();
        m = p.matcher(B);
        if (!m.matches())
        {
            System.out.println("数字不合法！");
            return;
        }
        System.out.println(A + " * " + B + " = "
            + bigIntMultiply(A, B, Math.max(A.length(), B.length())));
    }
}