校招笔试面试前,大家一般都会先去牛客网上刷刷题,《剑指offer》,《leetcode》走起来,然后初次入手,发现很多不会,不会到什么程度呢,连个想法都没有,于是就去讨论区看答案,然后java大神,c++大神会给出花式解答,他们喜欢在答案前加一句,简单的dp算法,递归就可以解决,巴拉巴拉。说的还是很详细的,然而代码并不能看懂,毕竟
人生苦短,我用python
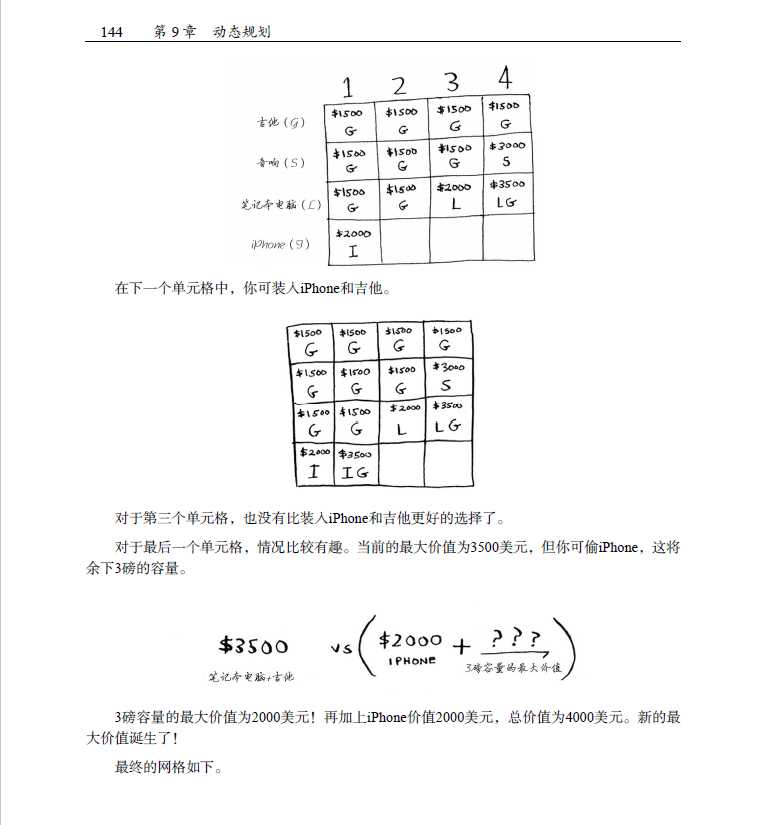
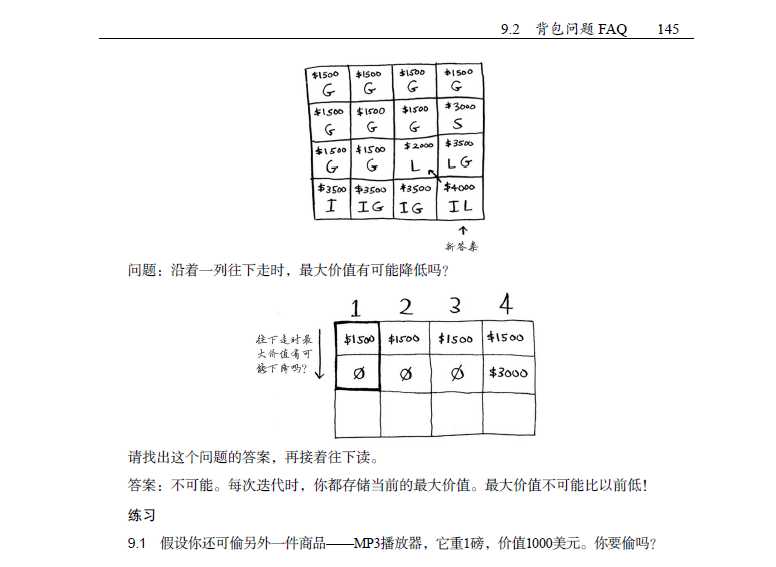
下面就先给大家举一些详细的例子来说说如何解决动态规划问题
首先,你要知道什么才能算动态规划问题,这里,推荐《算法图解》这本书,是基于python写的一本算法讲解书,内容非常简单,没未接触过算法的人也能看懂,我先直接引用这里的讲法:
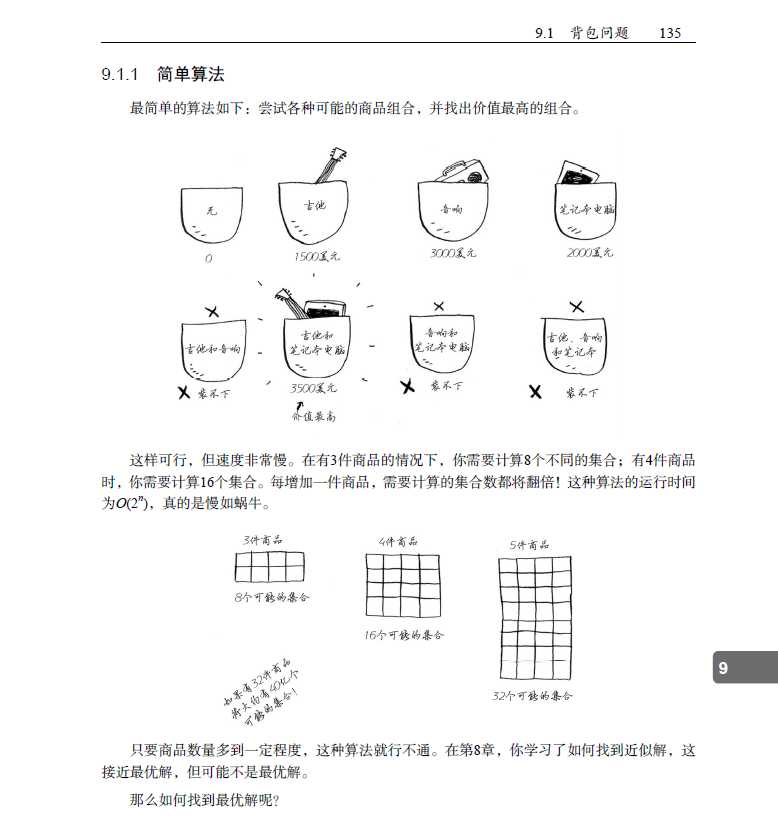
动态规划就是要将问题细分为小问题,然后再着手解决这些小问题。
例1:(题目来源于牛客网)
题目描述
输入描述:
输入为一个数字N,即需要拼凑的面额
输出描述:
输出也是一个数字,为组成N的组合个数。
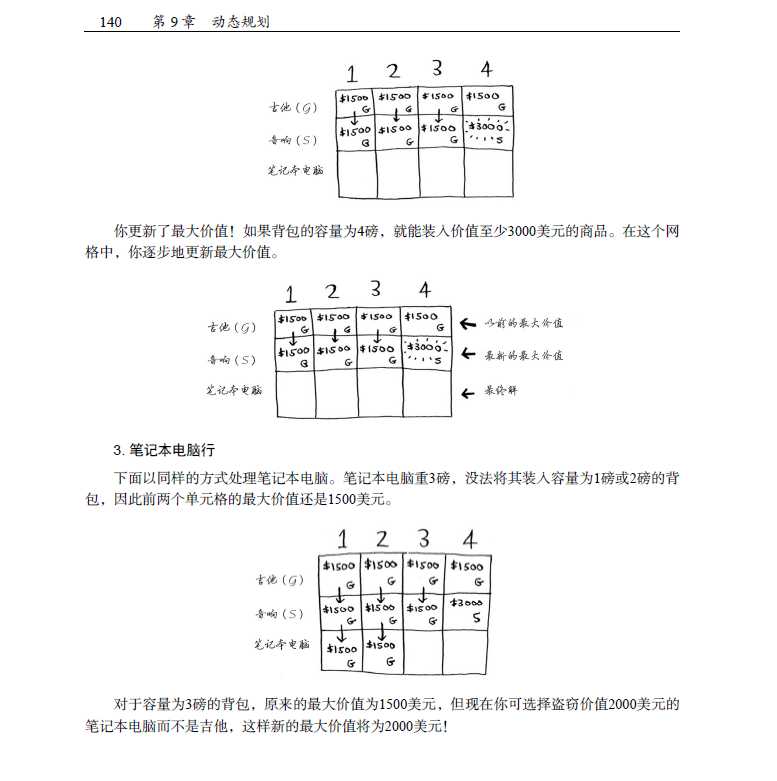
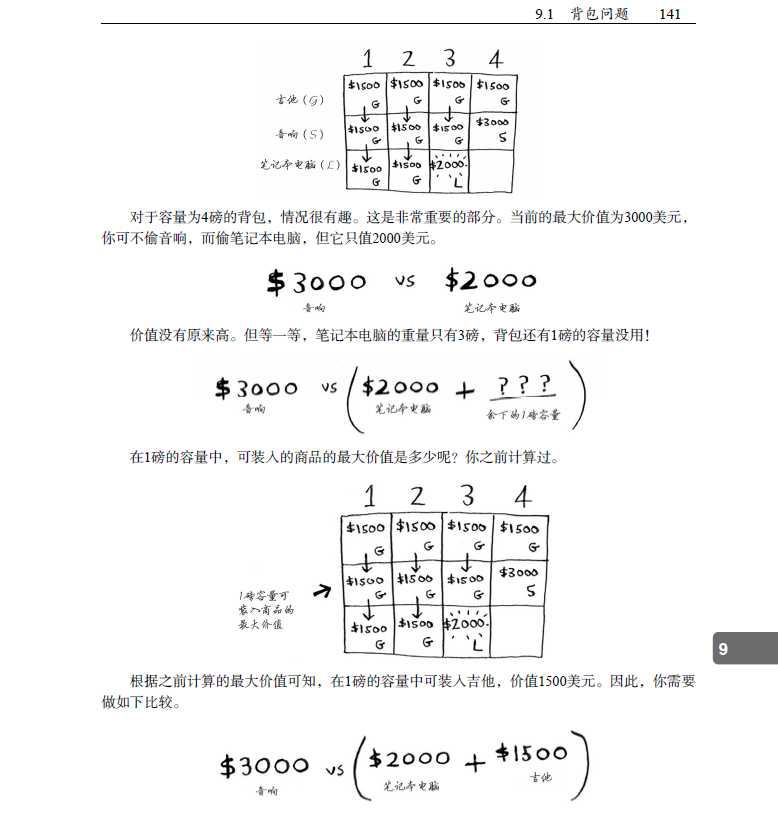
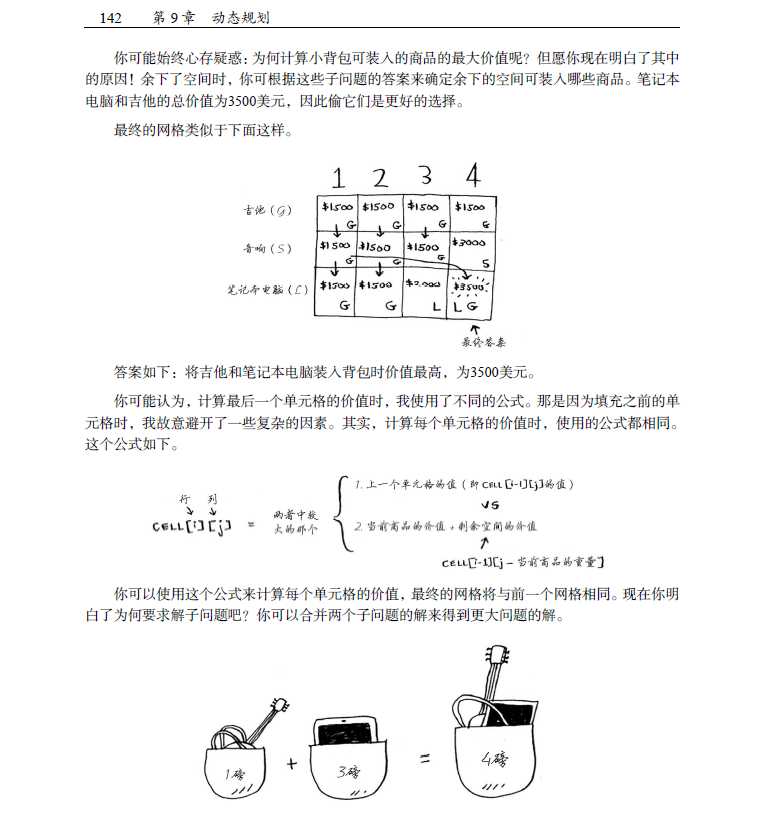
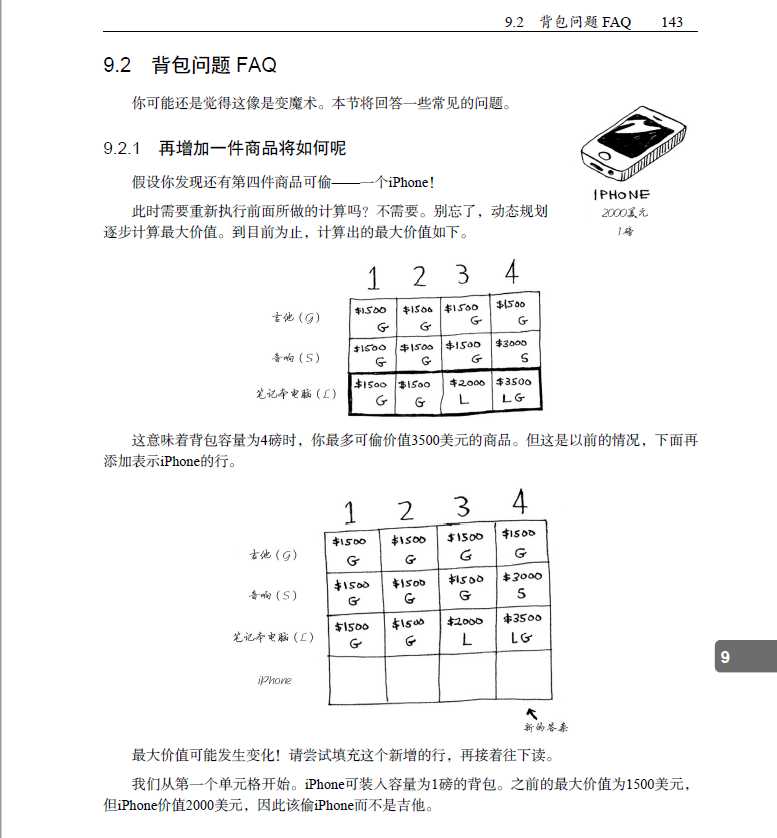
这可以视为一个动态回归问题解决,首先我们可以画一个dp表格
dp表的列数字表示要拼成的面额,行表示可以用哪几种面额的拼,比如说dp的一元行,5元列表示只用一元钱拼成5元钱只有一种方法,dp1元,5元行、6元列表示用币值1元和5元拼成6元的方法有两种,明显dp[1,:]=1,而若j>i,dp[i,j]=dp[i-1,j]+dp[i,j-i],例如dp[2,10]=dp[1,10]+dp[2,5], 这个表达式说明,用1元和5元的面额拼成10元的方法数=用1元拼成10元的方法数+用1元和5元拼成5元的方法数,因为面额6-9元拼成方法都是一样的,暂时没有更小的面额可供选择,这个公式便是这个算法的核心
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1元 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1元,5元 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 |
| 1,元,5元,10元 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 4 |
| 1,5,10,20元 | |||||||||||
| ,1,5,10,20,50元 | |||||||||||
| ,1,5,10,20,50,100元 |
代码如下
money=[1,5,10,20,50,100]
n = int(input())
li=[]
for i in range(n+1):
li.append(0)
li[0]=1
for i in money:
for j in range(n+1):
if j>=i:
li[j]=li[j]+li[j-i]
print(li)例2 来源于《剑指offer》
题目描述
简单来说就是求一个最大子串问题,也是一个典型的动态规划问题
思路:设F(i)是以array[i]为结束点的最大子向量(从0开始),比如说F(3)就是最后一个向量是7的最大子串,可知
F(i) = max(F(i-1)+array[i],array[i])
设res是所有字串中最大的那个,也就是我们最后要求的值
res = max(res,F(i))
代码:
def FindGreatestSumOfSubArray(array):
f = array[0]
res = array[0]
for i in range(1,len(array)):
f = max(f+array[i],array[i])
res = max(res,f)
return res这样便求得最后的解,不懂的话可以自己手写一下循环,多悟几次,日后使用起来就很方便啦
今天的文章动态规划算法dp_12个动态规划算法举例分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/77788.html