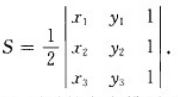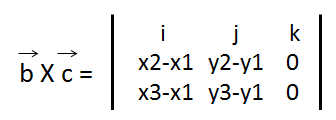向量的叉积求三角形面积_向量叉乘用矩阵计算

求三角形面积有诸多公式：
S = 1/2 ah
S = 1/2 absinC,
S = sqrt(p*(p-a)(p-b)(p-c))…

对于不同的场合，每个公式都有自己的优势，若是已知三个顶点坐标a(x1,y1), b(x2,y2), c(x3,y3)，若要求三点围成的三角形的面积，对计算机而言这个公式应该是最适合的：

S = 1/2 * |(x2 – x1) * (y3-y1) – (y2 – y1) * (x3 – x1)|

也可以展开成：
S = 1/2 * |(x1y2 + x2y3 + x3y1 – x1y3 – x2y1 – x3y2)|，
不过这种写法的乘法运算要相对多一些。

当然比较常见是写成行列式的样子：

相信许多人对这条公式并不陌生，下面我按照自己的理解推导一下这个公式：

第一种理解：

已知：三角形三个顶点及坐标a(x1,y1), b(x2,y2), c(x3,y3)

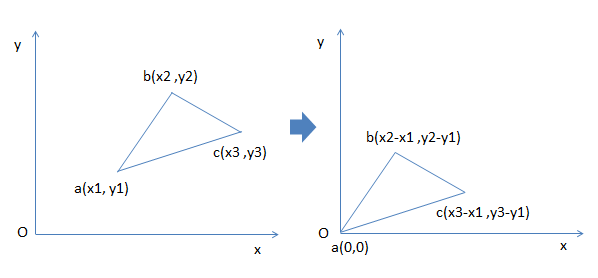
因为我们的目的是求面积，所以三角形的位置是无所谓的，首先，保持三角形整体不变，捉住三角形的某一个顶点，把它拖到坐标原点，如下图，这里就以点a为例，经过这样的操作后三点坐标就变成了a(0,0), b(x2-x1, y2-y1), c(x3-x1, y3-y1)。

把三角形整个捉走干什么呢，其实是为了得到两个向量：
把边ab，边ac分别看成向量b=(x2-x1, y2-y1, 0)和向量c=(x3-x1, y3-y1, 0)，这时先回忆一下向量叉乘：
两个向量叉乘的结果是一个新向量，这个新向量垂直于原向量组成的平面，并且新向量的长度等于原向量合成的平行四边形的面积。
因为向量b，向量c 在XOY平面，所以叉乘得到的向量一定落在Z轴上，设新向量d = (0 ,0 , z)，|z| 便是向量b，c 合成的平行四边形的面积，所以平行四边形的一半，|z|/2便是我们要求的三角形abc的面积。

有了这个思路，直接套上向量叉乘公式：

行列式的运算就不具体展示了，结果得：
向量d = (0, 0, (x2 – x1) * (y3-y1) – (y2 – y1) * (x3 – x1))。
根据上文，三角形abc的面积为|z|/2，即：
S = 1/2 * |(x2 – x1) * (y3-y1) – (y2 – y1) * (x3 – x1)|。

今天的文章向量的叉积求三角形面积_向量叉乘用矩阵计算分享到此就结束了，感谢您的阅读。