sobel算子边缘检测_常用的边缘检测算子

此篇文章主要介绍了Sobel算子的底层运算规律，和cv Harris的相关介绍

'''测试'''
import numpy as np

mm = np.array([1,2,3])
pow(mm,2)

array([1, 4, 9], dtype=int32)

Harris opencv 的对应代码
cv2.cornerHarris(src, blockSize, ksize, k[, dst[, borderType]])
参数类型
src – 输入灰度图像，float32类型
blockSize – 用于角点检测的邻域大小，就是上面提到的窗口的尺寸
ksize – 用于计算梯度图的Sobel算子的尺寸
k – 用于计算角点响应函数的参数k，取值范围常在0.04~0.06之间

注：Sobel算子是滤波算子的形式,利用快速卷积函数，简单有效，因此应用广泛
Sobel算子的本质，实际上是求图片的梯度值
优点：方法简单、处理速度快,并且所得的边缘光滑
缺点：Sobel算子并没有将图像的主体与背景严格地区分开来，换言之就是Sobel算子没有基于图像灰度进行处理
原理：
sobel算子的horizon水平检测Sob_x：
[[-1,0,1],
[-2,0,2],
[-1,0,1]]
sobel算子的vertical垂直检测 Sob_y：
[[1,2,1],
[0,0,0],
[-1,-2,-1]]
矩阵公式：
Gx = Sob_x *img.data Gy = Sob_y * img.data
G的运算采用L2 范数（此处实际上就是求某像素点的梯度值Grad）
节约时间可用L1范数（梯度公式的一阶导函数，数学原理是泰勒公式）
即求得每一个像素点的梯度
L2：G = np.sqrt(pow(Gx,2)+pow(Gy,2)
L1：G = |Gx|+|Gy|

        得到梯度值,若G大于阈值threshold,则说明有角点
        再由 theta = 1/tan(Gy/Gx)得到梯度的方向
        若theta 角度为0 代表图像有纵向边缘

'''sobel算子的实现'''
import numpy as np
import matplotlib.pyplot as plt
import cv2
%matplotlib inline
'''Sober算子,初始化'''
sob_x ,sob_y= [[-1,0,1],[-2,0,2],[-1,0,1]], \
              [[1,2,1],[0,0,0],[-1,-2,-1]]

'''图片读取并灰度化'''
img1 = cv2.imread('figures/image1.jpeg') #读取通道为BGR
img1_gray = cv2.cvtColor(img1,cv2.COLOR_BGR2GRAY) #BGR通道转为Gray,
# 类型type(img1_gray) numpy.ndarray,shape (390, 700)

plt.imshow(img1_gray,cmap='gray')
plt.show()

'''这里舍弃最外围的一圈像素点 实际sobel算子卷积了 388x698图片'''

# 切片操作，取第一个需要卷积的矩阵，其核心位置为【1，1】
d10 = img1_gray[0:10,0:10]
d1 = img1_gray[0:3,0:3]
sob_d1 = np.abs(np.sum(sob_x*d1)) +np.abs(np.sum(sob_y * d1))
d10,d1,f'最开始的卷积之后的值 = {sob_d1}'

(array([[135, 139, 143, 146, 148, 152, 156, 159, 161, 162],
        [135, 138, 142, 145, 148, 151, 155, 158, 161, 162],
        [134, 137, 142, 145, 147, 150, 154, 158, 161, 162],
        [134, 137, 141, 144, 147, 150, 154, 157, 161, 162],
        [134, 138, 142, 145, 147, 150, 155, 158, 161, 162],
        [136, 139, 143, 146, 148, 152, 156, 159, 161, 162],
        [137, 140, 144, 148, 150, 153, 157, 160, 161, 162],
        [138, 141, 145, 148, 151, 154, 158, 161, 161, 162],
        [144, 145, 146, 148, 150, 152, 154, 155, 160, 160],
        [144, 144, 145, 147, 148, 150, 152, 153, 160, 160]], dtype=uint8),
 array([[135, 139, 143],
        [135, 138, 142],
        [134, 137, 142]], dtype=uint8),
 '最开始的卷积之后的值 = 36')

'''定义一个卷积函数'''
def convolution_ndarray(kernal, data_gray):
    n, m = data_gray.shape  # (390, 700)
    img_new = np.zeros((n-2, m-2))
    for i in range(n-2 ):  # [0,387)
        temp_row = np.zeros(m-2)  # 700
        for j in range(m -2):  # [ 0,697)
            temp = data_gray[i:i + 3, j:j + 3]
            temp_row[j] = np.sum(np.multiply(kernal, temp))
        img_new[i] = temp_row
    return img_new



Gx = convolution_ndarray(sob_x,img1_gray)

Gy = convolution_ndarray(sob_y,img1_gray)
# L1范数
G_L1 = np.absolute(Gx) +np.absolute(Gy)
# L2范数
G_L2 = np.sqrt(pow(Gx,2)+pow(Gy,2))

# 255矩阵

ones = np.ones(G_L1.shape)*255 #ones.shape (387, 697)


plt.figure(figsize=(40,40))
plt.subplot(131)
plt.imshow(img1_gray, cmap='gray')
plt.title('Sober + row_data ')

Color_Reversal_1 = ones -G_L1 #颜色反转
plt.subplot(132)
plt.imshow(Color_Reversal_1,cmap='gray')
plt.title(' Sober + G_L1')

Color_Reversal_2 = ones-G_L2    #颜色反转
plt.subplot(133)
plt.imshow(G_L2,cmap='gray')
plt.title(' Sober +G_L2 ')
plt.show()

采用opencv 封装的Harris 角点检测方法检测角点
图像的角点检测
检测图像中的角点（几条边相交的位置)

1.Harris角点检测思想：边缘是在各个方向上都具有高密度变化的区域算法基本思想是使用一个固定窗口在图像上进行任意方向上的滑动，比较滑动前与滑动后两种情况，窗口中的像素灰度变化程度，如果存在任意方向上的滑动，都有着较大灰度变化，那么我们可以认为该窗口中存在角点。
角点的特征：
一个图像根据图像灰度值变化大小地不同可以分为三个级别：平坦区域、边缘位置和角点三类
>角点（特征点）当窗口向各方向移动，都会引起像素值发生很大变化的一个位置点；
>边缘特征: 仅当窗口单方向上来回移动，才会引起像素值发生较大变化的一个位置区域；
>平坦区域: 无论窗口移动方向如何，都不会引起像素值发生很大的变化的区域。
harris 角点检测的步骤
1.当窗口（小的图像片段）同时向 x 和 y 两个方向移动时，计算窗口内部的像素值变化量 d f(x,y) ;
2.对于每个窗口，都计算其对应的一个角点激活函数 G;
3.然后对该函数进行阈值处理，如果 G > threshold，表示该窗口对应一个角点特征.

2.Shi-Tomasi角点检测
Harris角点检测的改进版
Shi-Tomasi 发现，角点的稳定性其实和矩阵 M 的较小特征值有关

OpenCV 中的 Harris 角点检测参数
Open 中的函数 cv2.cornerHarris() 可以用来进行角点检测。参数如下:
　　• img – 数据类型为 float32 的输入图像。
　　• blockSize – 角点检测中要考虑的领域大小。
　　• ksize – Sobel 求导中使用的窗口大小
　　• k – Harris 角点检测方程中的自由参数,取值参数为 [0,04,0.06].
数学步骤：

计算每个blocksize大小的窗口的灰度值变化大小（但实际上最后间接的去求了自相似函数的特征值）。
blocksize是用来计算他的自相适性
算法:C (x,y ,dx,dy) =sum( {W(u,v) *( I(u,v) – I(u+dx,v+dy))} **2 )
其中 W(u,v)是以点( u , v ) (u,v)(u,v)为中心的窗口，既可以是常数，又可以是高斯加权函数。w(u,v)是一个权重矩阵，shape大小为 blocksize，若为常数，则为3×3的全1矩阵，
若为高斯，1/16【【1，2，1】，【2，4，2】，【1，2，1】】的矩阵
计算响应函数R
R=detM
(x,y)
−k⋅(trM
(x,y)
)
2
R值与阈值比较，判断每个窗口下是否包含角点。

原始图片（magic_cube)

magic_cube= cv2.imread('figures/magic_cube.jpg')  #cv2读取是BGR格式
magic_cube_gray = cv2.cvtColor(magic_cube,cv2.COLOR_BGR2GRAY)
corners_Harris = cv2.cornerHarris(magic_cube_gray,3,3,0.06) #shape (500, 500)
#Sobel运算x，y
cube_G_x = convolution_ndarray(sob_x,magic_cube_gray)
cube_G_y = convolution_ndarray(sob_y, magic_cube_gray)
cube_G_L1 =np.absolute(cube_G_x) +np.absolute(cube_G_y)

plt.figure(figsize=(40,40))
plt.subplot(131)
plt.imshow(magic_cube_gray,cmap ='gray')
plt.subplot(132)
plt.imshow(corners_Harris,cmap='gray')
plt.subplot(133)
plt.imshow(cube_G_L1,cmap='gray')
plt.show()
'''如下图所示，直接显示的检测效果并不理想，但sobel算子运算得到的边缘图十分明显 cube的上面灰度值与255较为接近，偏差不明显，之后使用threshold进行角点检测'''

'如下图所示，直接显示的检测效果并不理想，
cube的上面灰度值与255较为接近，偏差不明显，故而使用threshold'筛选数据

'''对该函数进行阈值处理，如果 G > threshold，表示该窗口对应一个角点特征.'''
threshold= 0.01*corners_Harris.max()
flag = corners_Harris > threshold


'''方法1，由np.where 直接找到 符合条件的array 下标'''
# where(condition, [x, y])
# x,y = np.where(flag) #返回tuple 返回了一个基于原本数据的地址索引 type() -> 2
x,y = np.where(flag)

corners_data1 = []
for i,j in zip(x,y):
    corners_data1.append(corners_Harris[i][j])
'''方法2，由 统计学习的数学运算方法传入一个由True，false组成的flag， 直接得到一个符合条件的一维数据'''
corners_data2 = corners_Harris[flag]


'''测试data_index 所指向的数据是否和corners_data所记录的符合的数据一致'''
corners_data1 == corners_data2
#数据比对均为True，说明由方法1和方法2获得的数据一样

array([ True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True])

'''对于方法2的解释说明'''
a = np.array([[1,2,3],[1,2,3]])
flag1 = np.array([[True,True,True],[False,True,False]])
b = a[flag1] #这种方法只是返回合格的数据，但并没有原始数据所在的下标，且形状为1维，适合label标签的选取分类

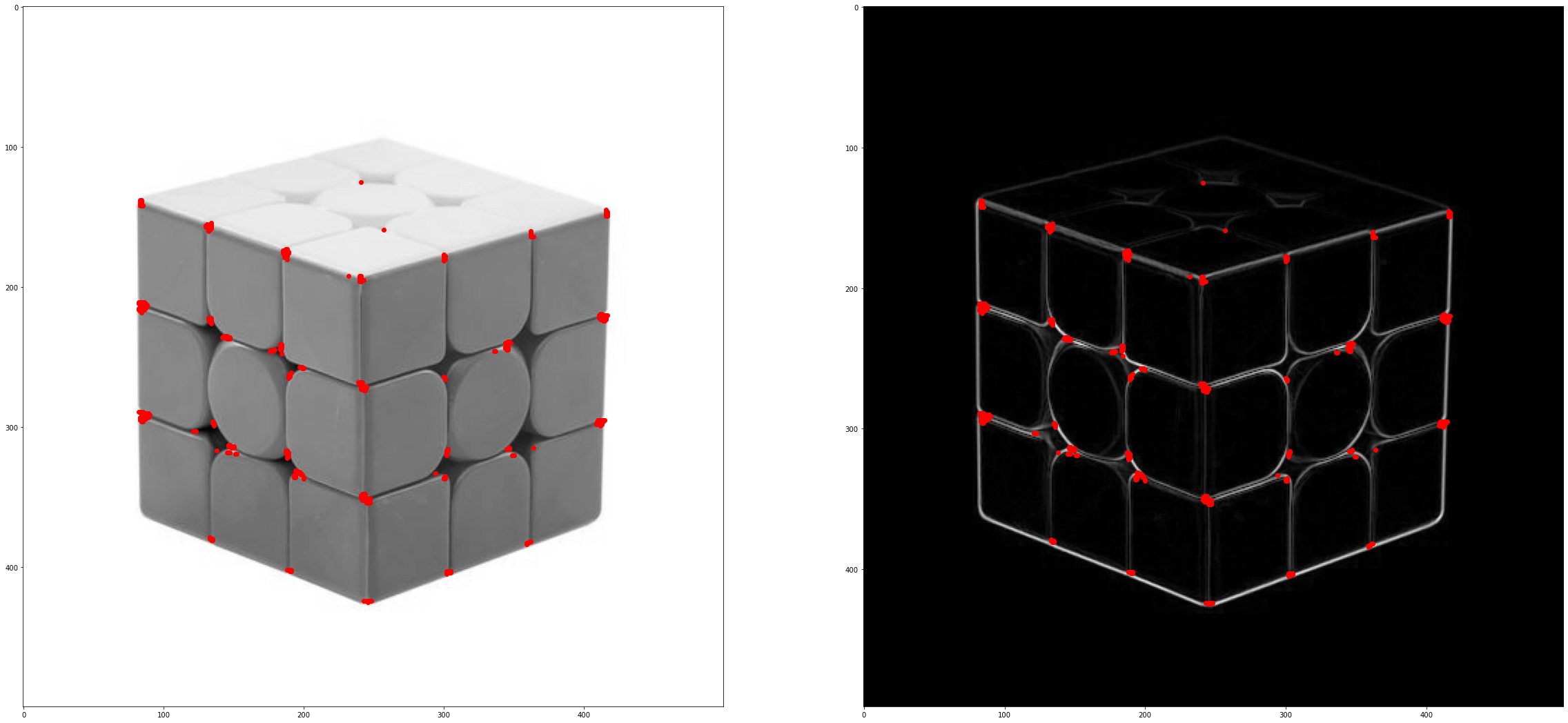
'''plot 绘制角点'''
plt.figure(figsize=(40,40))
plt.subplot(121)
plt.scatter(y,x,c = 'red')
plt.imshow(magic_cube_gray,cmap='gray')
plt.subplot(122)
plt.scatter(y,x,c = 'red')
plt.imshow(cube_G_L1,cmap='gray')
plt.show()
plt.savefig('figures/cube_Harris.png')

如上图所示,角点位置坐标全部标注为红色,数据在X,Y中保存对应的位置下标,实测所知,得到的数据x
,y转换后可以正常画图使用即x,y = y,x

推荐文章
主成分分析，独立成分分析，+t-SNE 分布随机可视化降维的对比
线性回归预测波士顿房价
基于逻辑回归的鸢尾花分类
数据表示和特征工程

参考文献
机器学习使用OpenCV、Python和scikit-learn进行智能图像处理(原书第2版)-(elib.cc) by (印)阿迪蒂亚·夏尔马(Aditya Sharma)(印)维什韦什·拉维·什里马利(Vishwesh Ravi Shrimali)(美)迈克尔·贝耶勒(Michael Beyeler)
Sobel算子，百度百科
角点检测Harris与Shi-Tomas
Harris数学计算过程与cornerHarris 参数说明

今天的文章sobel算子边缘检测_常用的边缘检测算子分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/78089.html

sobel算子边缘检测_常用的边缘检测算子

相关推荐

发表回复