多智能体强化学习之MADDPG

MADDPG（Multi-agent Deep Deterministic Policy Gradient）

MADDPG可以看作三部分，首先是DPG（Deterministic Policy Gradient），然后是DDPG（Deep Deterministic Policy Gradient），最后是MADDPG（Multi-agent Deeep Deterministic Policy Gradient）。我们需要逐一了解。

1、什么是DPG？

DPG是在连续动作空间上采用确定策略进行Policy gradient 的一种算法，它使用的是价值函数的梯度的期望。

2、为什么要用deterministic policy，和stochastic policy gradient 相比有什么优势 ？

在stochastic policy gradient 中我们需要在状态空间和动作空间上采样，每个状态可能有多个动作，当动作的维度比较大的时候就会需要特别多的采用数据，但是如果采用deterministic policy就只需要对状态采样即可，因此更加高效。

采用deterministic policy可以避免使用importance sampling。这一点会在之后说明。

采用deterministic policy gradient 可以得到一种根据价值函数梯度的期望更新的方法，计算更为方便，也能更好的解决连续动作空间上的控制问题。

3、为什么会想到用DPG？

value based 的算法中DQN性能出众，但是尽管DQN可以做到直接通过高维的输入来学习控制策略，却只能应用在低维、离散的动作空间上，因为它需要找到能最大化价值的动作 $\mathrm{argmax}Q(s,a)$ ，这一点在连续的动作空间上是很难做到的。常见的应用在连续动作空间上的RL算法是policy gradient，之前学习actor critic算法的时候我们已经知道policy gradient是将策略参数化然后通过更新策略的参数来最大化回报，通过一系列运算最后得出了策略梯度定理，也找到了更新策略参数的方向。现在我们需要解决DQN无法处理连续动作空间的问题，我们同样参数化一个策略，但是在更新参数的时候其实可以有这样一个直觉上的想法，既然连续动作空间上难以做 $\mathrm{argmax}Q(s,a)$ ，那么就向着能够最大化Q的方向更新policy的参数应该也能优化策略，因为不同的状态有着不同的更新方向，所以可以对他们取平均，即：
$$\begin{array}{rl}& {\theta }^{k+1}={\theta }^k+\alpha {\mathbb{E}}_{s\sim {\rho }^{\mu }k}\left[{\nabla }_{\theta }{Q}^{{\mu }^k}\left(s,{\mu }_{\theta }(s)\right)\right]\\ & {\theta }^{k+1}={\theta }^k+\alpha {\mathbb{E}}_{s\sim {\rho }^{\mu }k}\left[{{\nabla }_{\theta }{\mu }_{\theta }(s){\nabla }_a{Q}^{{\mu }^k}(s,a)|}_{a={\mu }_{\theta }(s)}\right]\end{array}\text{\hspace{1em}(11.3.1)}$$
此处状态服从分布：${\rho }^{\mu }$ ，策略为parameterized deterministic policy：${\mu }_{\theta }$

这里不难发现，如果不是采用deterministic policy而是采用stochastic policy那么参数更新就变成了熟悉的policy gradient：

$$\begin{array}{r}{\theta }^{k+1}={\theta }^k+\alpha {\mathbb{E}}_{s\sim {\rho }^{\pi },a\sim {\pi }_{\theta }}\left[{\nabla }_{\theta }\ln {\pi }_{\theta }(a|s)Q^{\omega }\left(s,a\right)\right]\end{array}\text{\hspace{1em}(11.3.2)}$$
在DPG的论文中给出了一些证明，上述理念是可行的，一些关键的步骤如下：

首先在deterministic policy下的objective是：
$$\begin{array}{rl}J\left({\mu }_{\theta }\right)& ={\int }_{\mathcal{S}}{\rho }^{\mu }(s)r\left(s,{\mu }_{\theta }(s)\right)\mathrm{d}s\\ & ={\mathbb{E}}_{s\sim {\rho }^{\mu }}\left[r\left(s,{\mu }_{\theta }(s)\right)\right]\end{array}\text{\hspace{1em}(11.3.3)}$$
为了书写简便，上标的策略都省略了 $\theta$ 。对它求梯度：
$$\begin{array}{rl}{\nabla }_{\theta }J\left({\mu }_{\theta }\right)& ={{\int }_{\mathcal{S}}{\rho }^{\mu }(s){\nabla }_{\theta }{\mu }_{\theta }(s){\nabla }_a{Q}^{\mu }(s,a)|}_{a={\mu }_{\theta }(s)}\mathrm{d}s\\ & ={\mathbb{E}}_{s\sim {\rho }^{\mu }}\left[{{\nabla }_{\theta }{\mu }_{\theta }(s){\nabla }_a{Q}^{\mu }(s,a)|}_{a={\mu }_{\theta }(s)}\right]\end{array}\text{\hspace{1em}(11.3.4)}$$
不难发现，向着价值函数增加方向更新策略的参数确实能起到优化效果。

接下来就会想到deterministic policy的思想能否用到 actor critic上，但是这里存在一个问题，之前的actor critic 都是 on policy的，exploration 主要依赖stochastic policy，现在使了deterministic policy就会导致exploration 不充分，解决这个问题的直接思路就是用 off policy actor critic，Sutton在书中提到过，几乎所有的off policy算法都会用到重要度采样（importance sampling）的方法。我们首先来看一下采用随机策略的off policy actor critic算法，为了衡量一个策略的表现我们需要定义一个“performance”：
$$\begin{array}{rl}{J}_{\beta }\left({\pi }_{\theta }\right)& ={\int }_{\mathcal{S}}{\rho }^{\beta }(s)V^{\pi }(s)\mathrm{d}s\\ & ={\int }_{\mathcal{S}}{\int }_{\mathcal{A}}{\rho }^{\beta }(s){\pi }_{\theta }(a|s)Q^{\pi }(s,a)\mathrm{d}a\mathrm{d}s\end{array}\text{\hspace{1em}(11.3.5)}$$
对其求梯度可以得到：
$$\begin{array}{rl}{\nabla }_{\theta }{J}_{\beta }\left({\pi }_{\theta }\right)& \approx {\int }_{\mathcal{S}}{\int }_{\mathcal{A}}{\rho }^{\beta }(s){\nabla }_{\theta }{\pi }_{\theta }(a|s)Q^{\pi }(s,a)\mathrm{d}a\mathrm{d}s\\ & ={\mathbb{E}}_{s\sim {\rho }^{\beta },a\sim \beta }\left[\frac{{\pi }_{\theta }(a|s)}{{\beta }_{\theta }(a|s)}{\nabla }_{\theta }\log {\pi }_{\theta }(a|s)Q^{\pi }(s,a)\right]\end{array}\text{\hspace{1em}(11.3.6)}$$
第一个约等号是因为舍去了对Q求梯度的那一项。最后确实用到了重要度采样，具体的推导过程可以参考离散动作下的off policy actor critic：
$$\begin{array}{rl}{\nabla }_{\mathbf{u}}{J}_{\gamma }(\mathbf{u})\approx \mathbf{g}(\mathbf{u})& =\sum _{s\in \mathcal{S}}{d}^b(s)\sum _{a\in \mathcal{A}}{\nabla }_{\mathbf{u}}\pi (a|s)Q^{\pi ,\gamma }(s,a)\\ & =\mathrm{E}\left[\sum _{a\in \mathcal{A}}{\nabla }_{\mathbf{u}}\pi (a|s)Q^{\pi ,\gamma }(s,a)|s\sim d^b\right]\\ & =\mathrm{E}\left[\sum _{a\in \mathcal{A}}b(a|s)\frac{\pi (a|s)}{b(a|s)}\frac{{\nabla }_{\mathbf{u}}\pi (a|s)}{\pi (a|s)}{Q}^{\pi ,\gamma }(s,a)|s\sim d^b\right]\\ & =\mathrm{E}[\rho (s,a)\psi (s,a)Q^{\pi ,\gamma }(s,a)\left|s\sim d^b,a\sim b(\cdot |s)\right]\\ & ={\mathrm{E}}_b\left[\rho \left(s_t,a_t\right)\psi \left(s_t,a_t\right)Q^{\pi ,\gamma }\left(s_t,a_t\right)\right]\end{array}\text{\hspace{1em}(11.3.7)}$$
如果采用确定策略的off policy actor critic 则推导过程如下：
$$\begin{array}{rl}{J}_{\beta }\left({\mu }_{\theta }\right)& ={\int }_{\mathcal{S}}{\rho }^{\beta }(s)V^{\mu }(s)\mathrm{d}s\\ & ={\int }_{\mathcal{S}}{\rho }^{\beta }(s)Q^{\mu }\left(s,{\mu }_{\theta }(s)\right)\mathrm{d}\\ & \\ {\nabla }_{\theta }{J}_{\beta }\left({\mu }_{\theta }\right)& \approx {\int }_{\mathcal{S}}{\rho }^{\beta }(s){\nabla }_{\theta }{\mu }_{\theta }(a|s)Q^{\mu }(s,a)\mathrm{d}s\\ & ={\mathbb{E}}_{s\sim {\rho }^{\beta }}\left[{{\nabla }_{\theta }{\mu }_{\theta }(s){\nabla }_a{Q}^{\mu }(s,a)|}_{a={\mu }_{\theta }(s)}\right]\end{array}\text{\hspace{1em}(11.3.8)}$$
对比之后可以看出来 deterministic off policy actor critic可以省去重要度采样！形式上更加简便了。至此我们基本上就解决了DQN不能处理连续动作空间的问题了。

4、什么是DDPG？

DDPG就是把神经网络用到了DPG上。对actor critic算法而言就是用一个神经网络来获得动作，并且不断优化这个网络，使得它输出的动作向着能够最大化价值的方向调整。

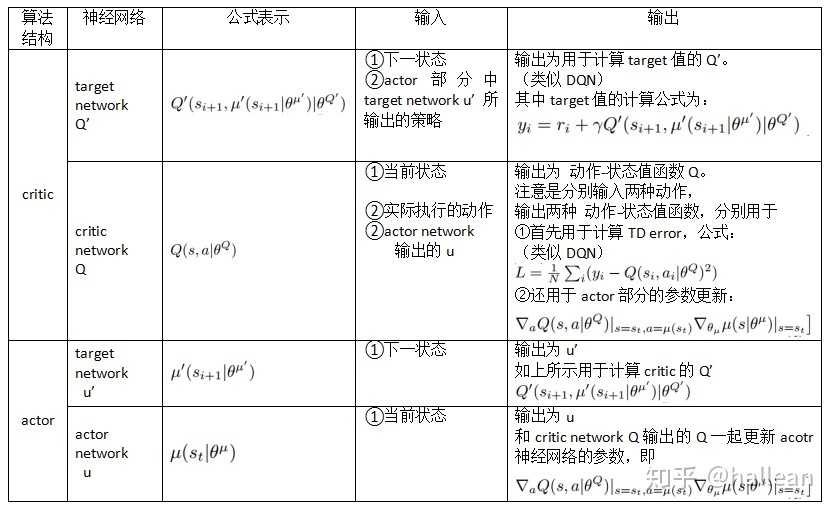
DDPG也采用了memory replay的方法，和DQN不同的DDPG总共用了4个网络，actor、actor_target、critic、critic_target，target网络的作用和DQN时相同的，都是为了使训练更稳定。网络之间的关系可以参考下表：

class Actor(nn.Module):
	def __init__(self, state_dim, action_dim, max_action):
		super(Actor, self).__init__()

		self.l1 = nn.Linear(state_dim, 400)
		self.l2 = nn.Linear(400, 300)
		self.l3 = nn.Linear(300, action_dim)
		
		self.max_action = max_action

	
	def forward(self, state):
		a = F.relu(self.l1(state))
		a = F.relu(self.l2(a))
		return self.max_action * torch.tanh(self.l3(a))


class Critic(nn.Module):
	def __init__(self, state_dim, action_dim):
		super(Critic, self).__init__()

		self.l1 = nn.Linear(state_dim, 400)
		self.l2 = nn.Linear(400 + action_dim, 300)
		self.l3 = nn.Linear(300, 1)


	def forward(self, state, action):
		q = F.relu(self.l1(state))
		q = F.relu(self.l2(torch.cat([q, action], 1)))
		return self.l3(q)

这里需要注意：Critic需要输入state和 action，所以在网络中有 q = F.relu(self.l2(torch.cat([q, action], 1)))这么一步。还有一个需要注意的是：Actor虽然是一个确定策略但是不要忘记这是定义在连续动作空间上的，所以它的输出并不是 $1\times 1$ 的，而是一个向量！！但是Critic的输出是 $1\times 1$ 的，因为它代表价值！

接下来是更新过程：

target_Q = self.critic_target(next_state, self.actor_target(next_state))
target_Q = reward + (not_done * self.discount * target_Q).detach()

# Get current Q estimate
current_Q = self.critic(state, action)

# Compute critic loss
critic_loss = F.mse_loss(current_Q, target_Q)

# Optimize the critic
self.critic_optimizer.zero_grad()
critic_loss.backward()
self.critic_optimizer.step()

# Compute actor loss
actor_loss = -self.critic(state, self.actor(state)).mean()

# Optimize the actor 
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()

因为我们需要将policy，也就是Actor网络向着 ${\nabla }_{\theta }{Q}^{{\mu }^k}\left(s,{\mu }_{\theta }(s)\right)$ 方向更新，所以：actor_loss = -self.critic(state, self.actor(state)).mean()负号是方便做gradient ascent。

5、什么是MADDPG？

​ MADDPG就是在多智能体领域采用DDPG。

6、为什么要采用MADDPG？

在多智能体领域，直接应用传统的算法会遇到诸多困难，Q-Learning会受到环境不稳定性的影响，policy gradient在有多个agent的时候方差会加大。具体而言就是每个agent在训练过程中policy都会不断变化，对于某一个agent而言，其他的agents都是环境的一部分，所以整个环境都将变得不稳定，例如转移概率这样受策略影响的量。因此experience replay也不能直接使用了。但是如果我们能够知道其agent的policy，action那么就有：
$$\begin{array}{r}P\left(s^{\prime }|s,a_1,\dots ,a_N,{\mathbf{\pi }}_1,\dots ,{\mathbf{\pi }}_N\right)=P\left(s^{\prime }|s,a_1,\dots ,a_N\right)=P\left(s^{\prime }|s,a_1,\dots ,a_N,{\mathbf{\pi }}_1^{\prime },\dots ,{\mathbf{\pi }}_N^{\prime }\right)\end{array}\text{\hspace{1em}(11.6.1)}$$
就可以利用其他agent的策略来学习。

7、MADDPG是怎么实现的？

MADDPG的想法其实并不复杂，仍然是采用actor critic的结构，只不过是在critic部分加入了其他agent的信息，原先DPG是：
$$\begin{array}{rl}{\nabla }_{\theta }J\left({\mu }_{\theta }\right)& ={\mathbb{E}}_{s\sim {\rho }^{\mu }}\left[{{\nabla }_{\theta }{\mu }_{\theta }(s){\nabla }_a{Q}^{\mu }(s,a)|}_{a={\mu }_{\theta }(s)}\right]\end{array}\text{\hspace{1em}(11.7.1)}$$
现在变成了：
$$\begin{array}{r}{\nabla }_{{\theta }_i}J\left(u_i\right)=E_{x,a\sim D}\left[{\nabla }_{{\theta }_i}{u}_i\left(a_i|o_i\right){\nabla }_{a_i}{Q}_i^u\left(x,a_1,\dots ,a_n\right)|a_i=u_i\left(o_i\right)\right]\end{array}\text{\hspace{1em}(11.7.2)}$$
其中 $x=\left(o_1,o_2,\dots o_n\right)$ ，包含了所有agent的观测状态（observation)，critic相应地就变成了：
$$\begin{array}{r}\mathcal{L}\left({\theta }_i\right)={\mathbb{E}}_{\mathbf{x},a,r,{\mathbf{x}}^{\prime }}\left[{\left(Q_i^{\mathbf{\mu }}\left(\mathbf{x},a_1,\dots ,a_N\right)-y\right)}^2\right],y=r_i+{\gamma Q_i^{{\mathbf{\mu }}^{\prime }}\left({\mathbf{x}}^{\prime },a_1^{\prime },\dots ,a_N^{\prime }\right)|}_{a_j^{\prime }={\mathbf{\mu }}_j^{\prime }\left(o_j\right)}\end{array}\text{\hspace{1em}(11.7.3)}$$

class Critic(nn.Module):
    def __init__(self, n_agent, dim_observation, dim_action):
        super(Critic, self).__init__()
        obs_dim = dim_observation * n_agent
        act_dim = self.dim_action * n_agent

        self.FC1 = nn.Linear(obs_dim, 1024)
        self.FC2 = nn.Linear(1024+act_dim, 512)
        self.FC3 = nn.Linear(512, 300)
        self.FC4 = nn.Linear(300, 1)

    # obs: batch_size * obs_dim
    def forward(self, obs, acts):
        result = F.relu(self.FC1(obs))
        combined = th.cat([result, acts], 1)
        result = F.relu(self.FC2(combined))
        return self.FC4(F.relu(self.FC3(result)))


class Actor(nn.Module):
    def __init__(self, dim_observation, dim_action):
        super(Actor, self).__init__()
        self.FC1 = nn.Linear(dim_observation, 500)
        self.FC2 = nn.Linear(500, 128)
        self.FC3 = nn.Linear(128, dim_action)

    # action output between -2 and 2
    def forward(self, obs):
        result = F.relu(self.FC1(obs))
        result = F.relu(self.FC2(result))
        result = F.tanh(self.FC3(result))
        return result

可以看到在Critic网络中有：obs_dim = dim_observation * n_agent和 act_dim = self.dim_action * n_agent其他部分和DDPG几乎相同。

8、MADDPG存在哪些问题，可以怎么改进？

（1）因为我们需要知道其他agent的policy，这是一个很强的假设，为了解决它我们可以用一个函数来拟合其他agent的策略（inferring policy）。

（2）我们利用了其他agent的policy来学习，这样有可能会过拟合，比如说几个agent之间本来是合作的关系，如果突然变成了竞争关系那么之前学到的policy就会受到很大影响，为了解决这个问题，我们可以采用 ensemble policy，即每个episode都随机的选取一部分sub-policy。

参考资料

1、《Deterministic Policy Gradient Algorithms》
2、《Off-Policy Actor-Critic》
3、《Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments》
4、《CONTINUOUS CONTROL WITH DEEP REINFORCEMENT LEARNING》
5、知乎
6、知乎

今天的文章多智能体强化学习之MADDPG分享到此就结束了，感谢您的阅读。