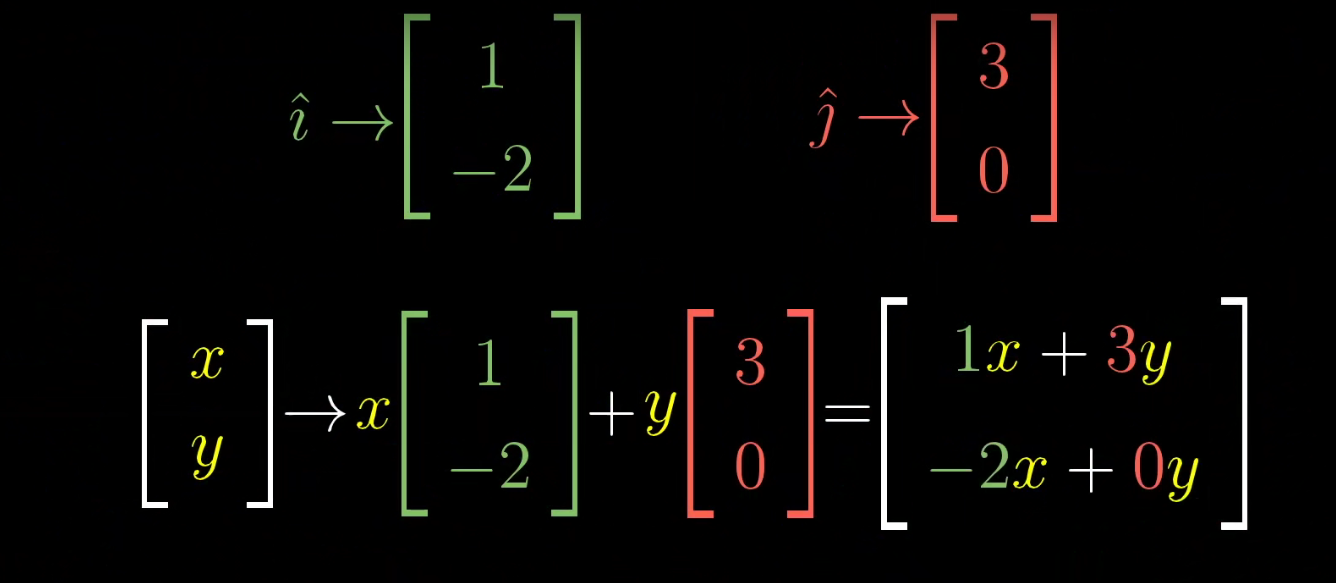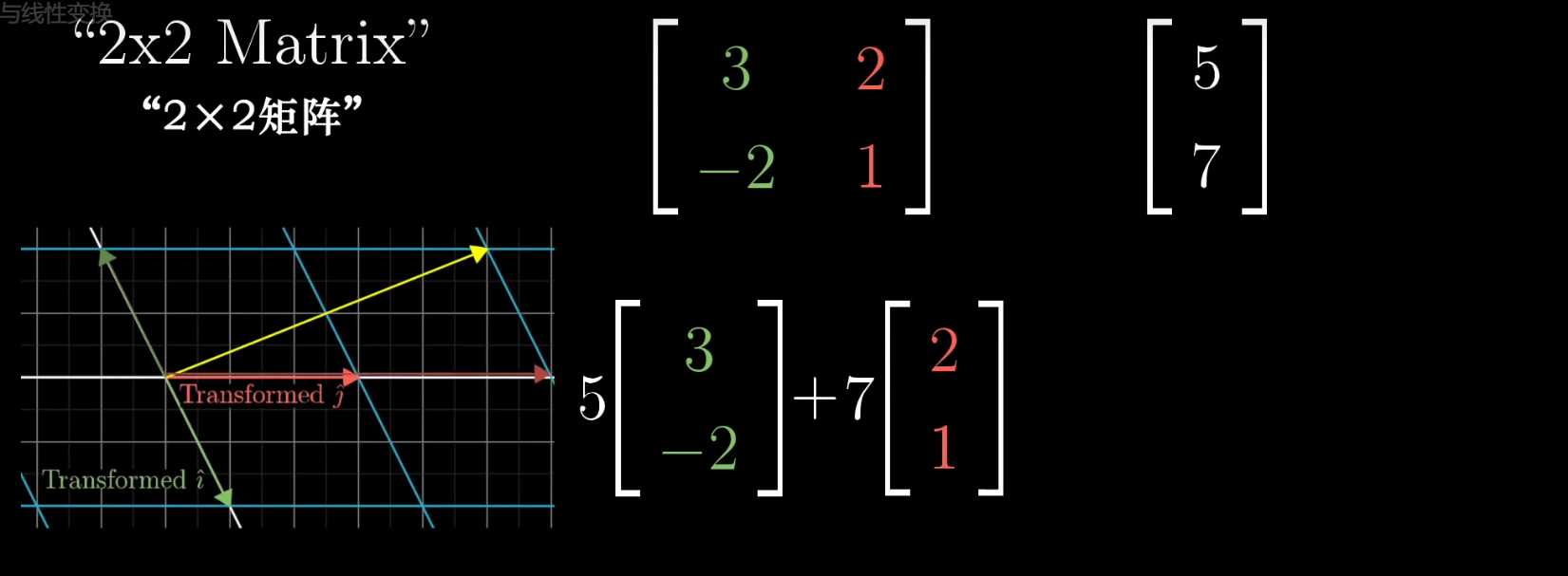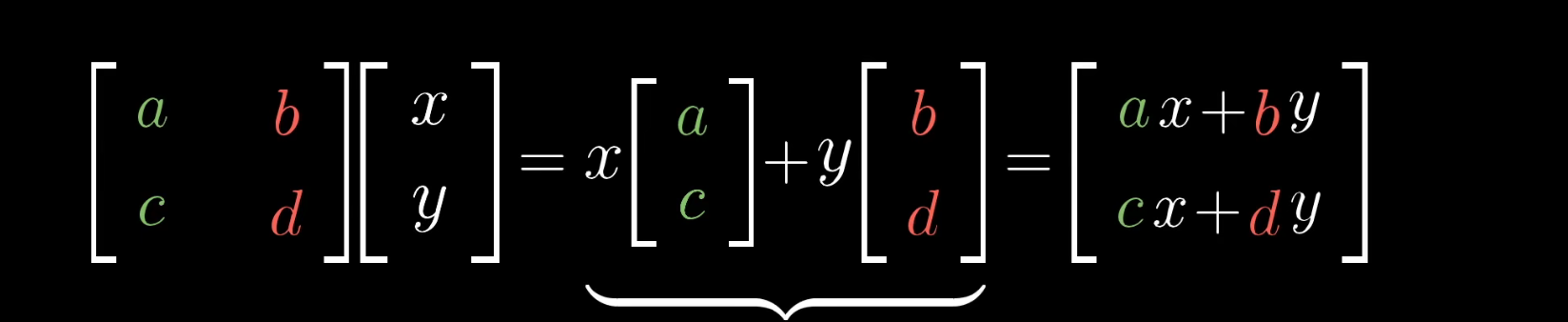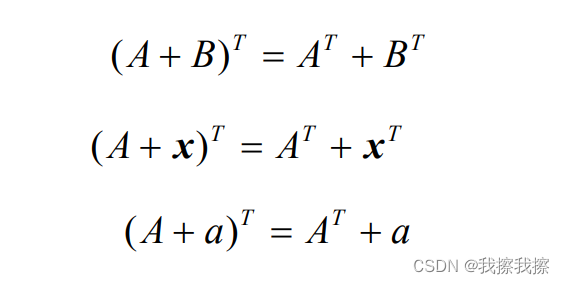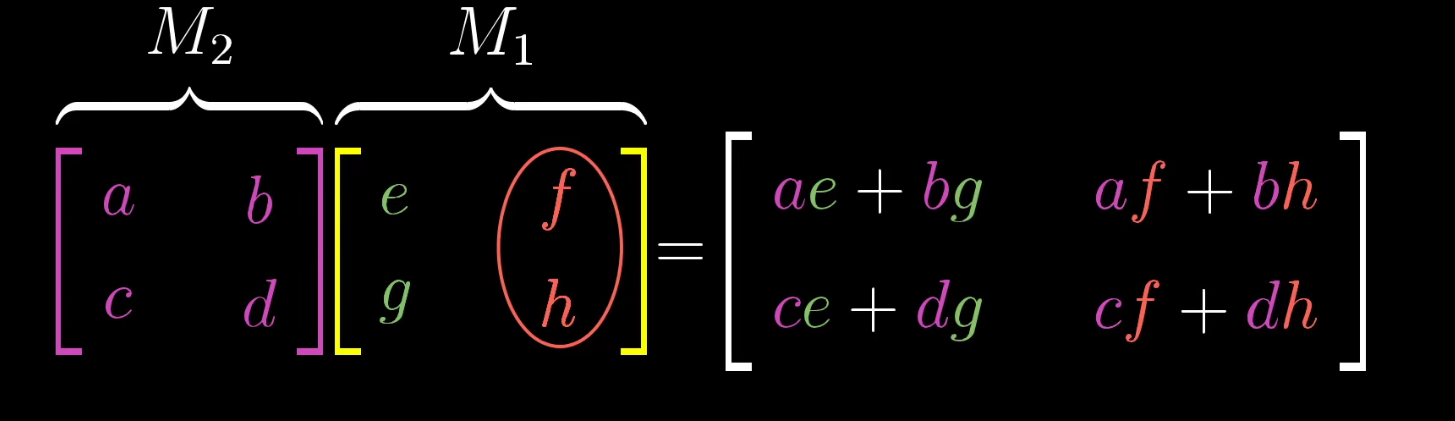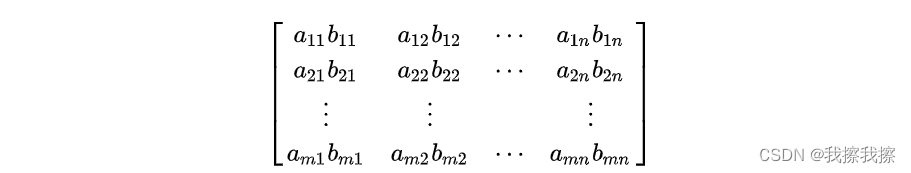文章目录
一:线性变换
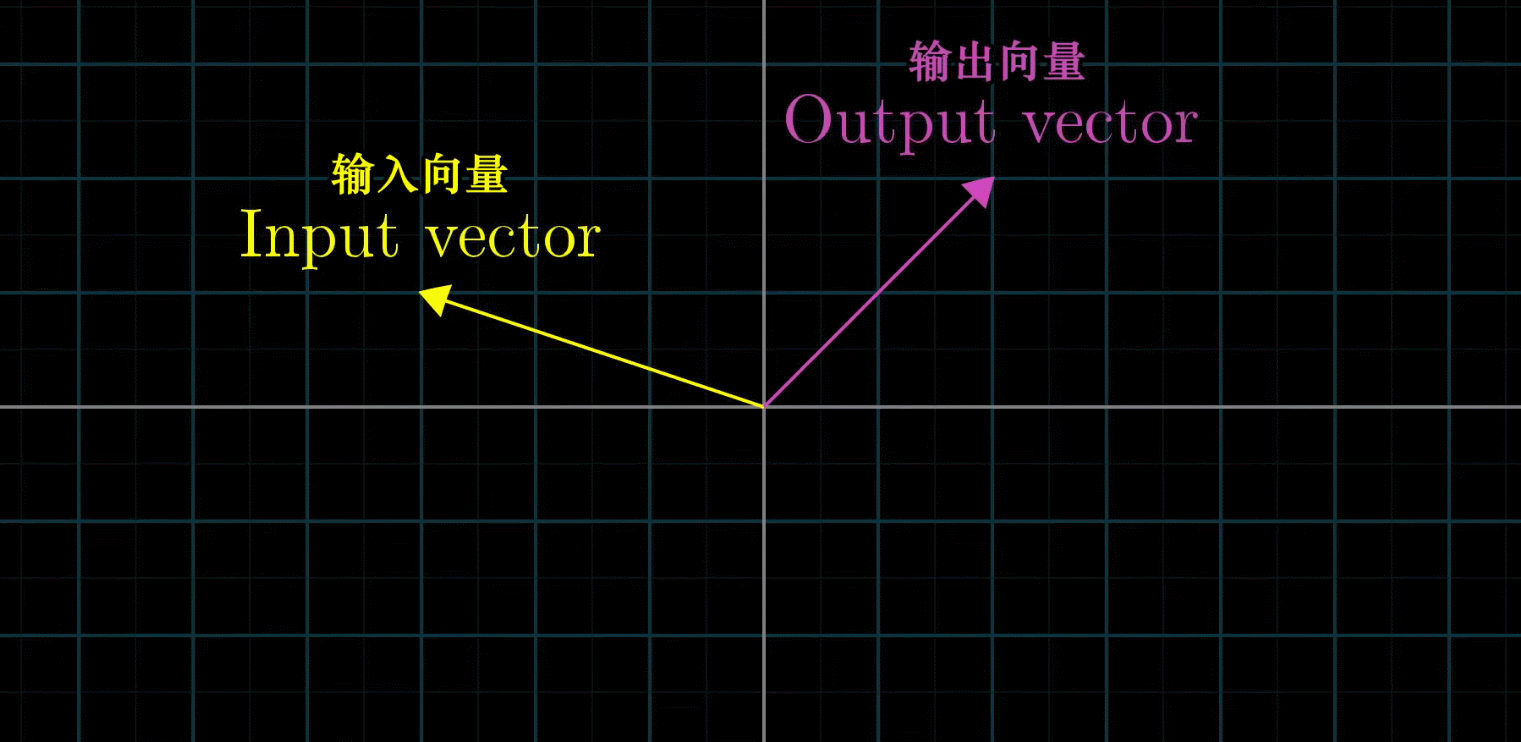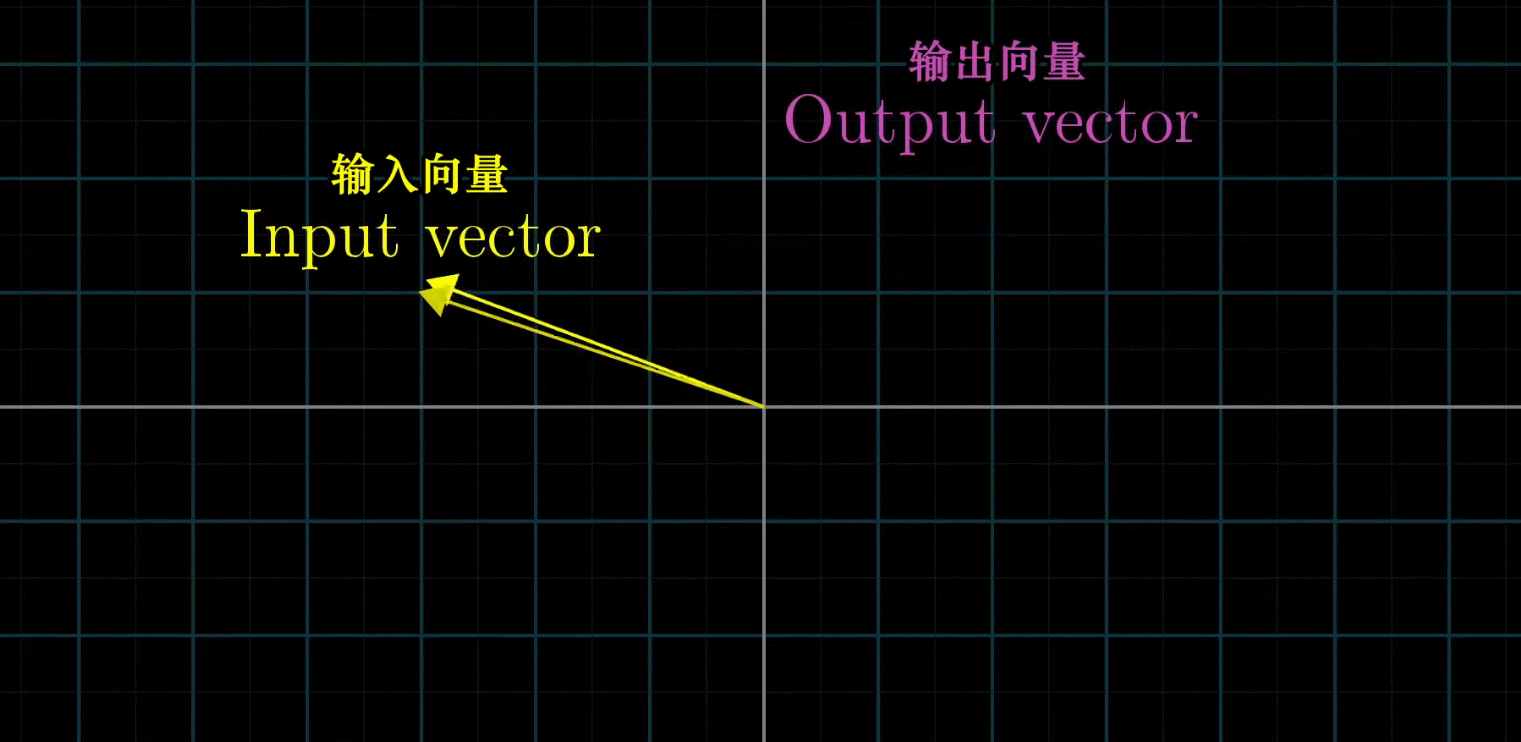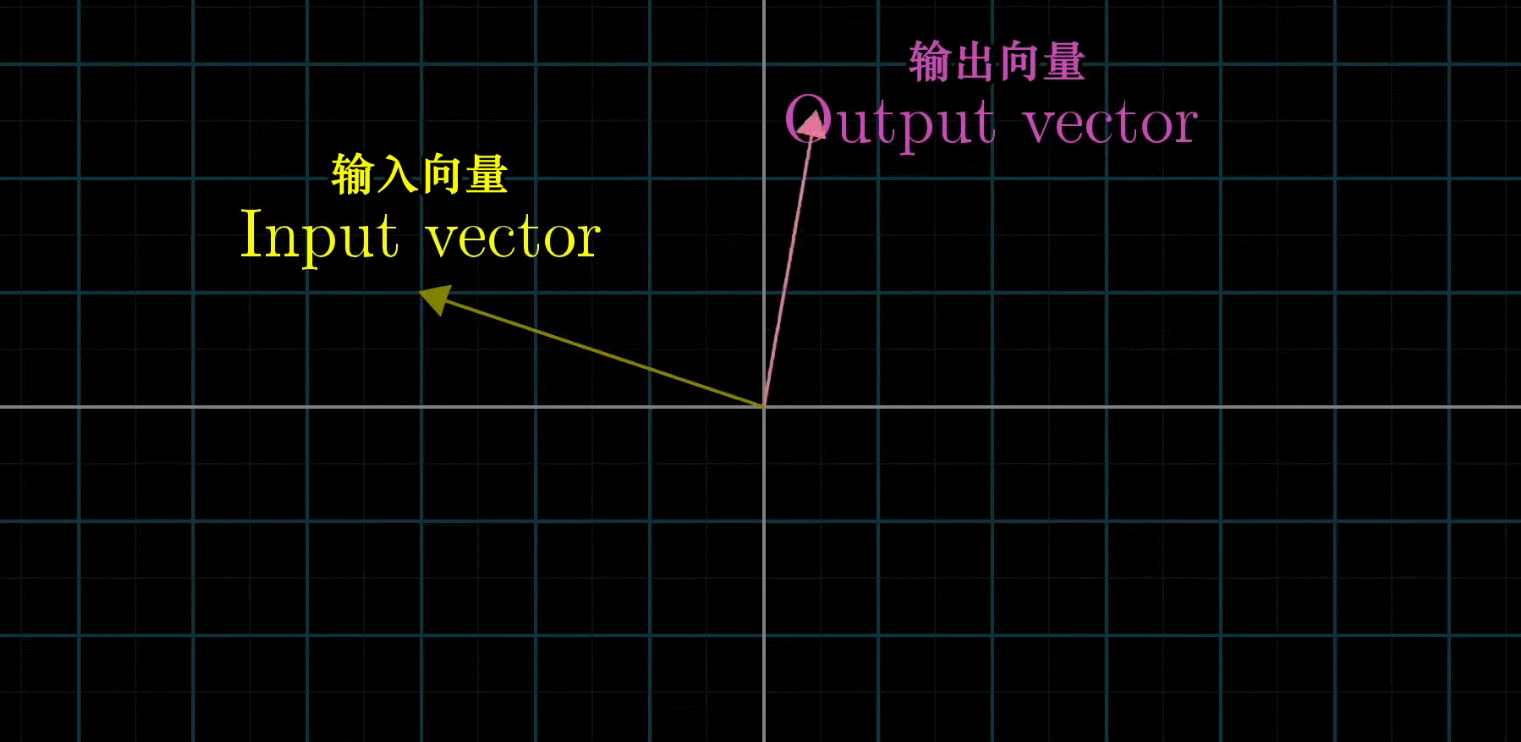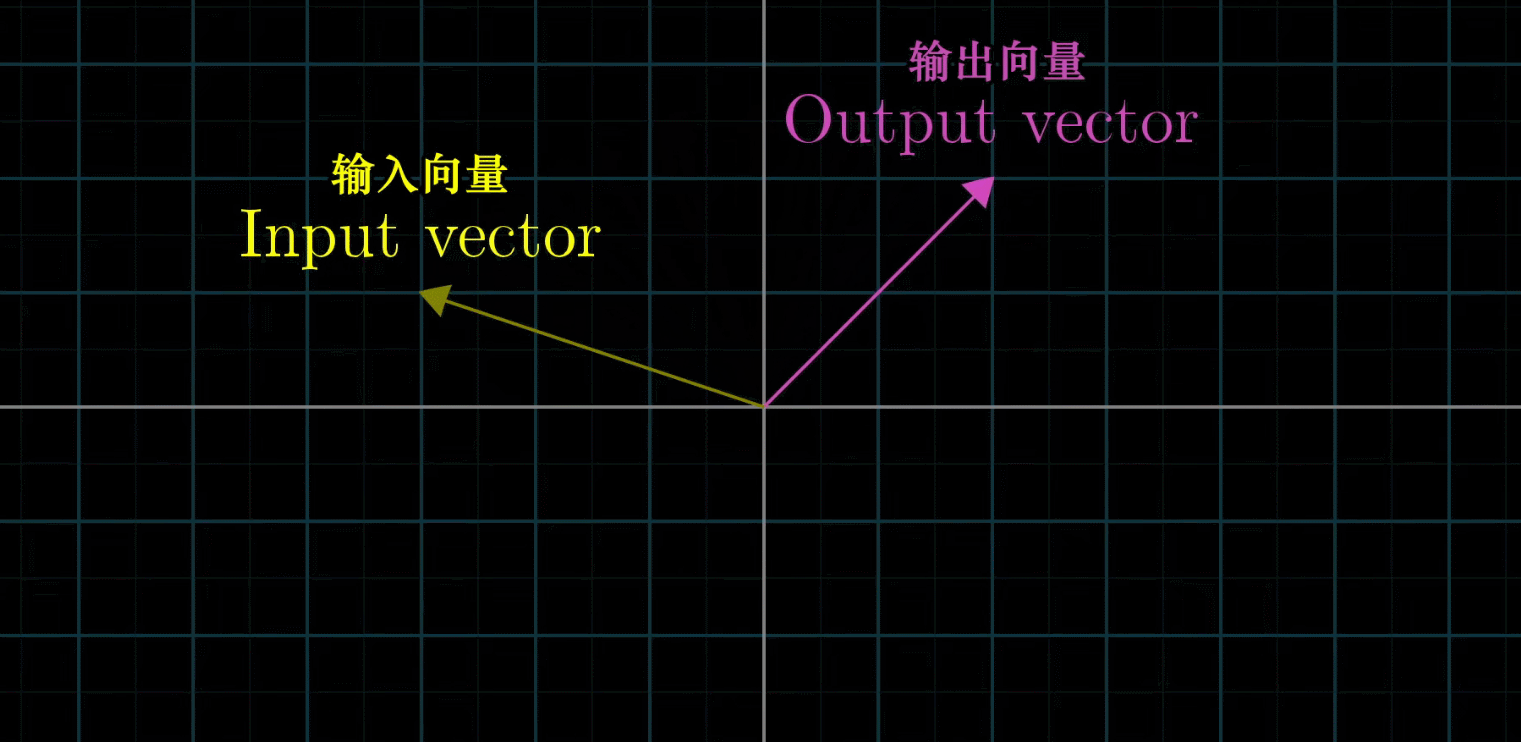
变换其实就是函数,接收输入内容然后输出结果
变换相对于函数来讲,无疑增添了一种运动的感觉
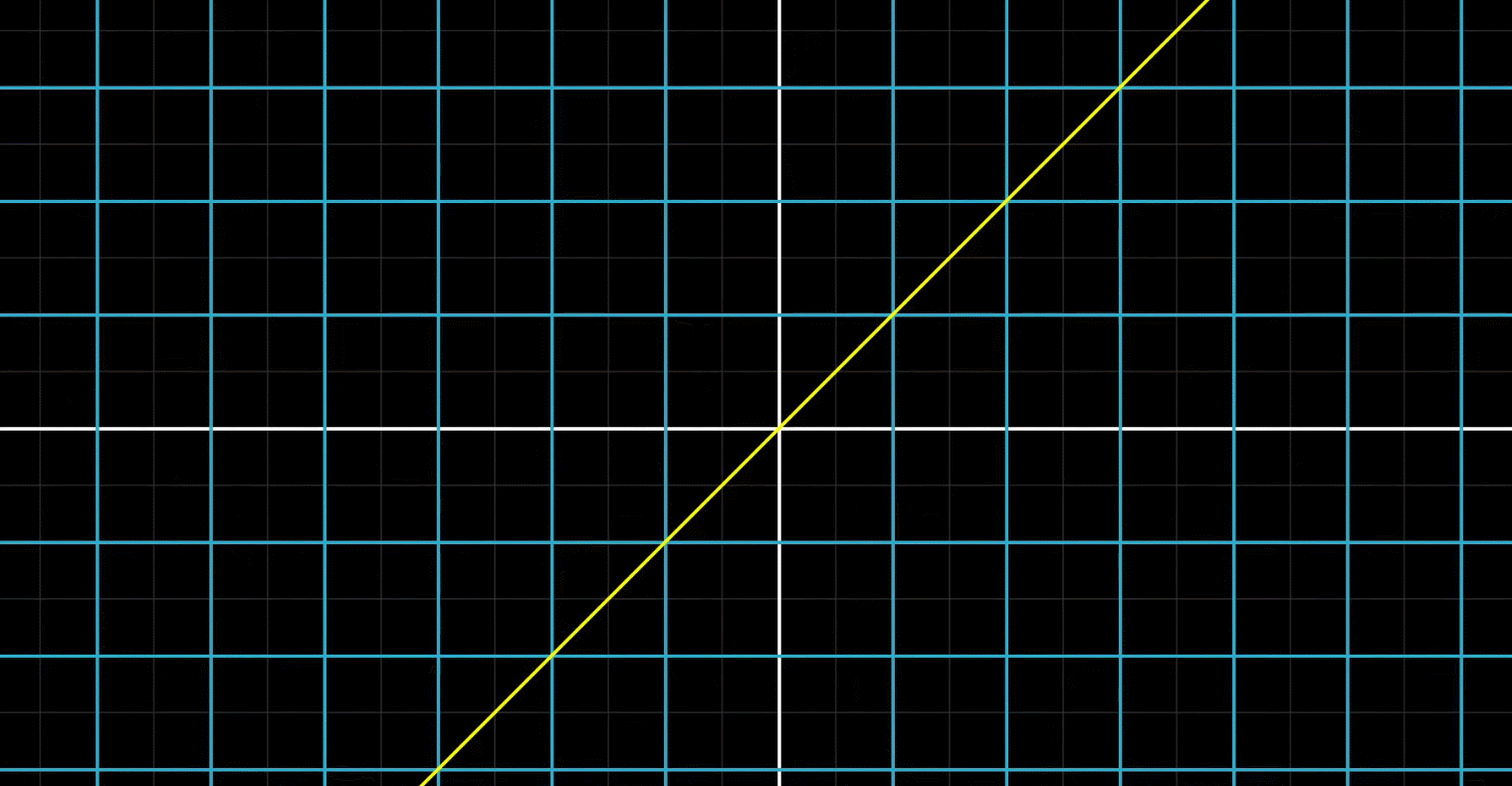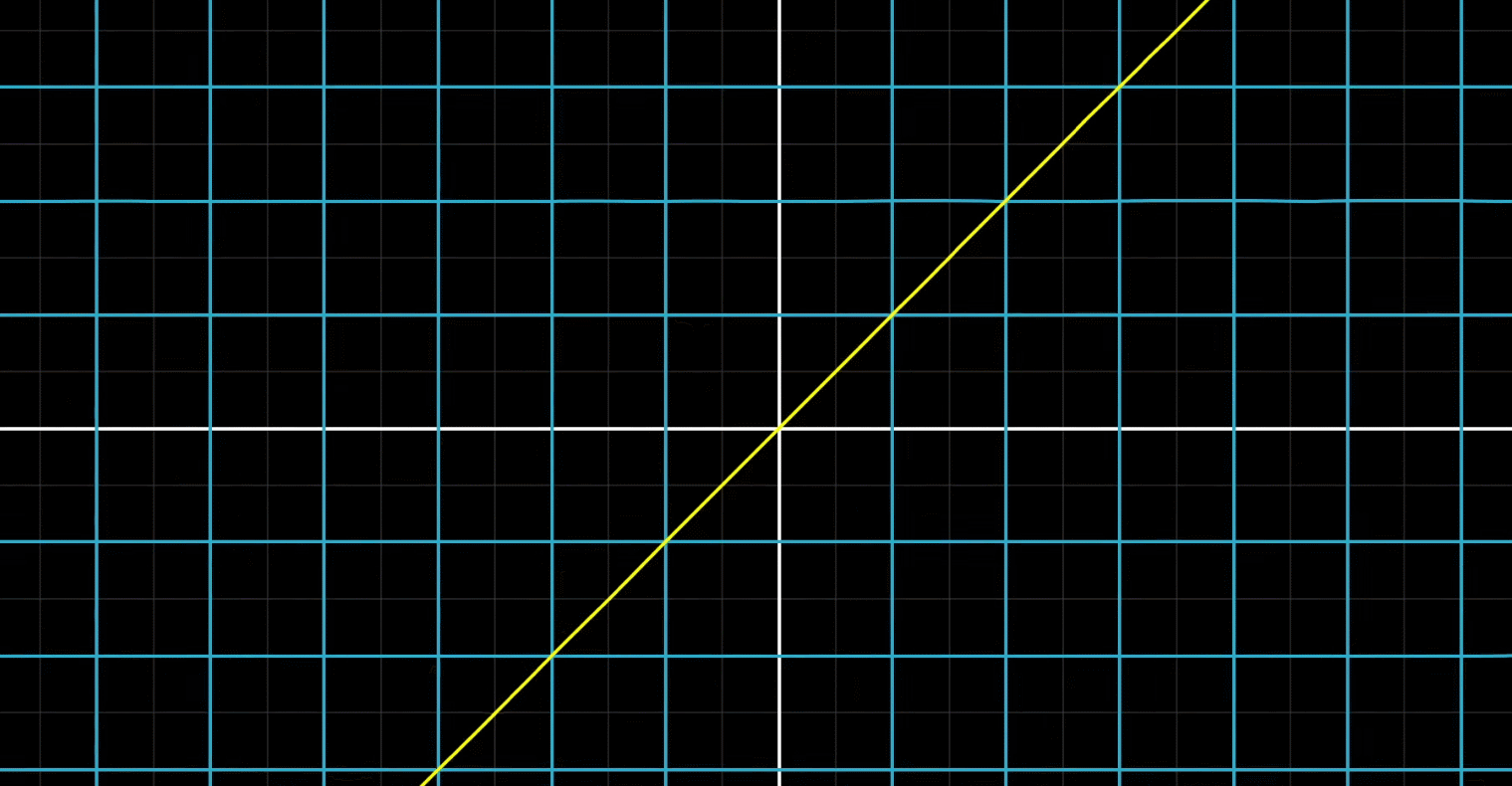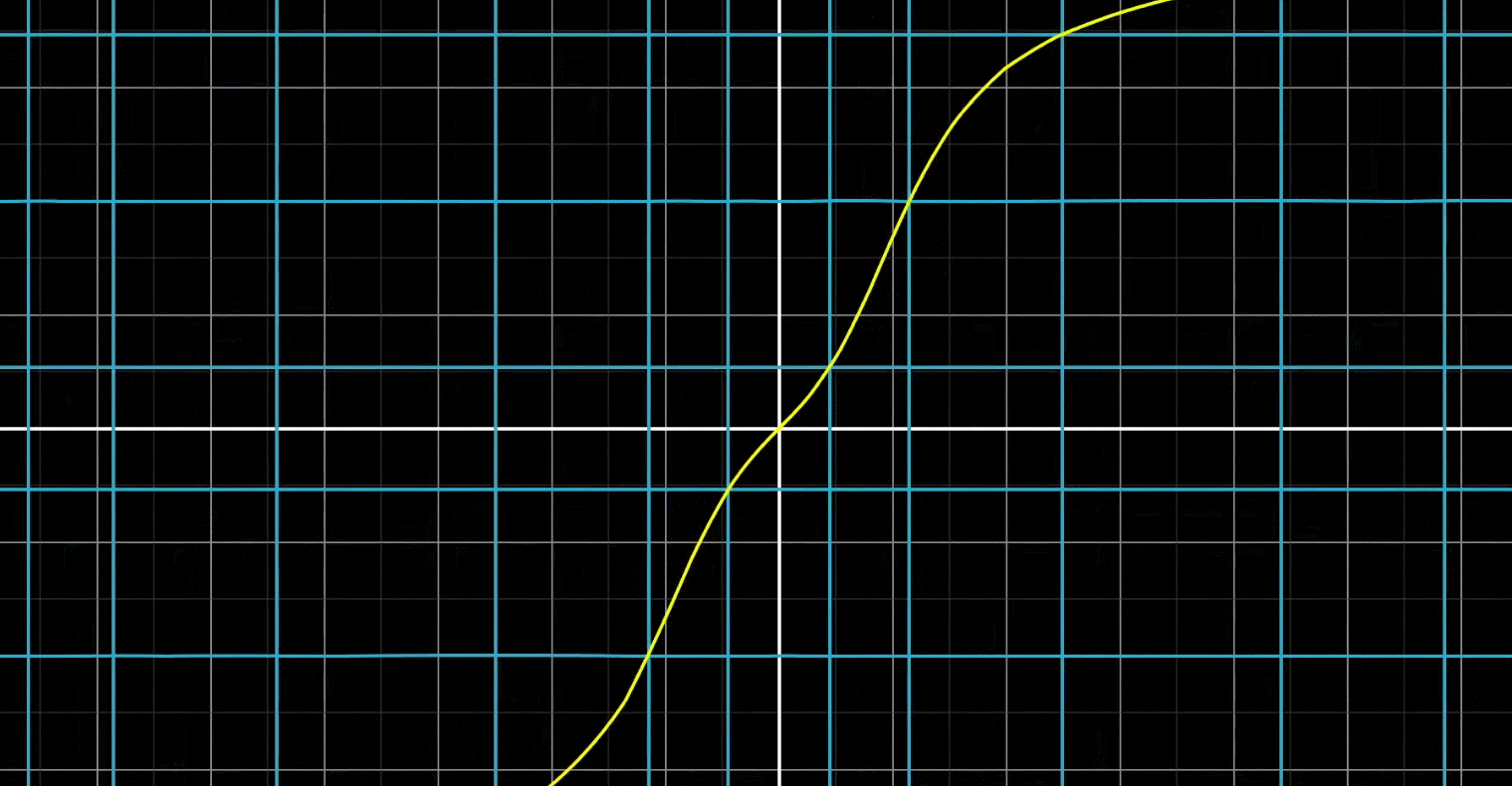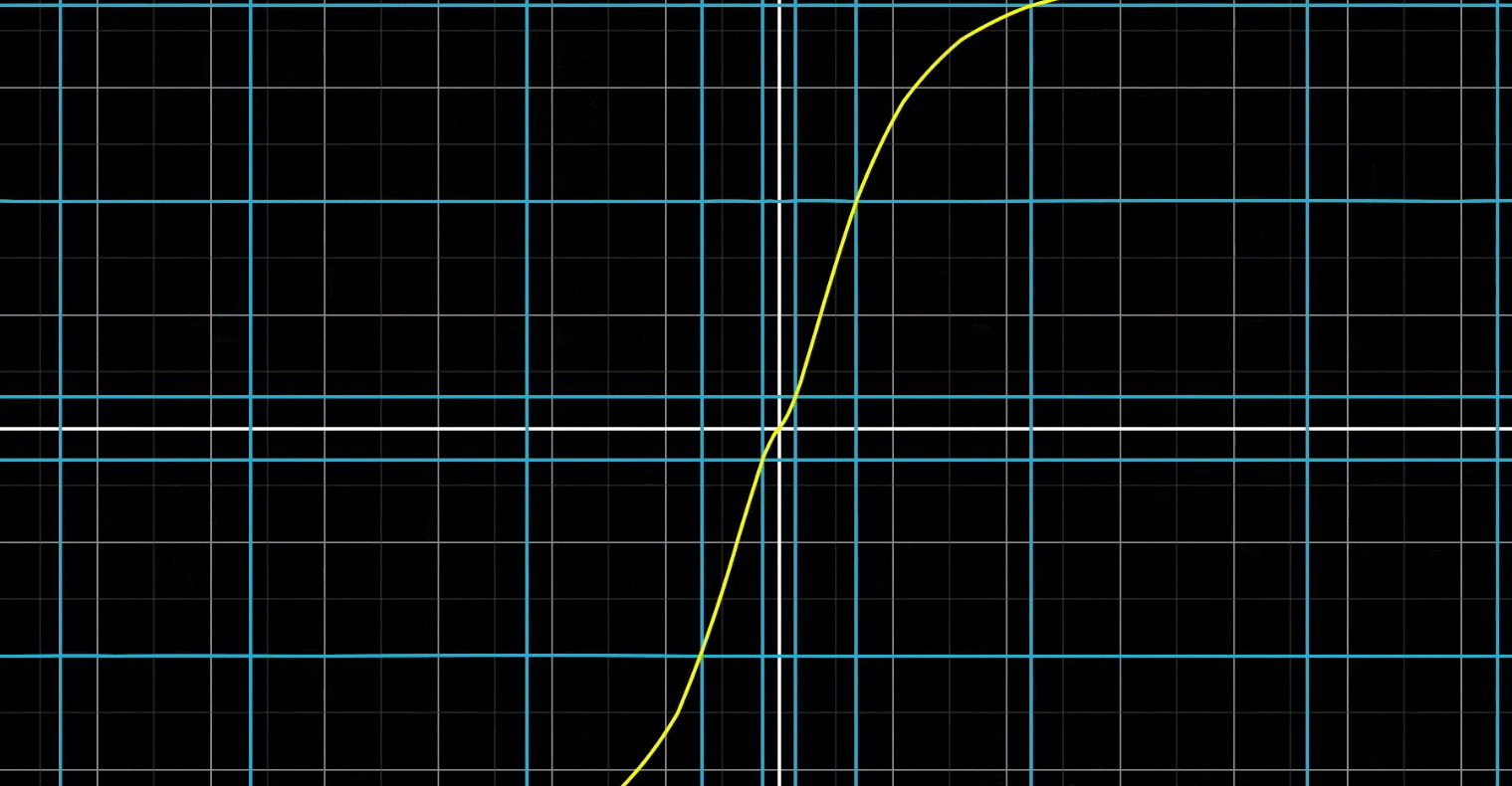
线性变换:输入一个向量经过变换之后再输出对应的向量。线性变换是一种保持网格平行且等距分布的变换
如果一个变换具有以下三条性质,我们就称它是线性的
-
1:直线在变换后仍然是直线,不能弯曲(下面动图是反例,直线被弯曲)
-
2:原点必须固定(下面是反例,直线虽然还是直线,但是原点移动了)
-
3:对角线也不能弯曲(下面第一张图看起来好像是线性的,但是第二张图揭示了对角线弯曲了)
-
线性的对立面就是非线性,所以非线性变换会把向量扭曲
- 复平面 f ( z ) = z 2 2 f(z)=\frac{z^{2}}{2} f(z)=2z2变换
- 复平面 f ( z ) = e z f(z)=e^z f(z)=ez变换
二:矩阵
(1)概念
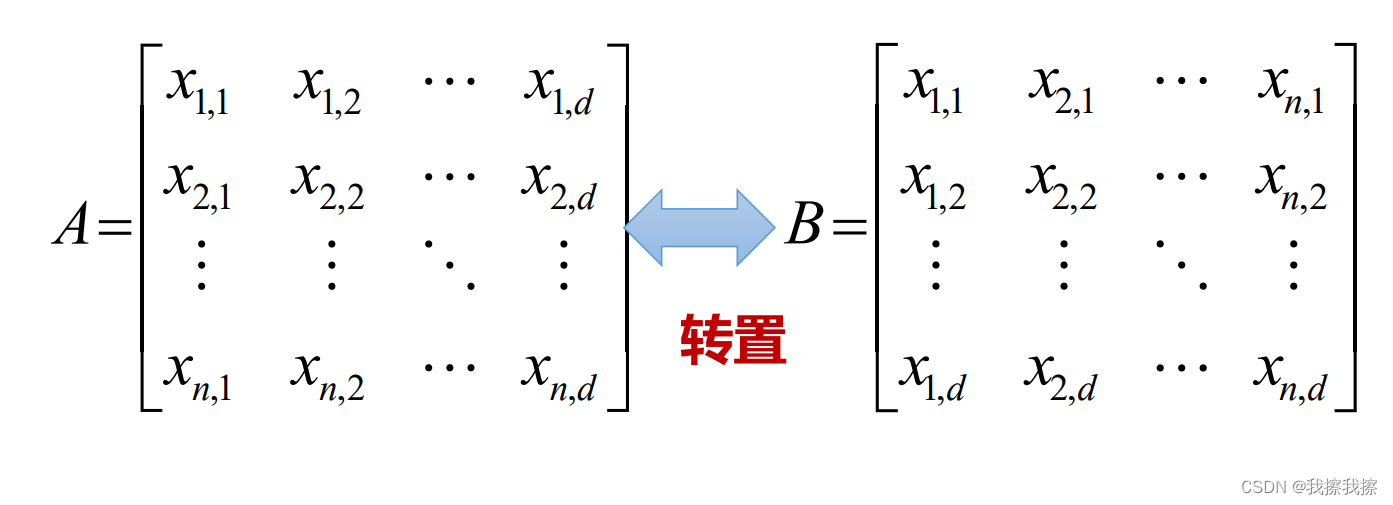
矩阵:有 m m m× n n n个数 x i j x_{ij} xij排成的 m m m行 n n n列的数称之为 m m m× n n n矩阵,记作
- A i , : A_{i,:} Ai,:表示矩阵 A A A的行向量(第 i i i行)
- A : . j A_{:.j} A:.j表示矩阵 A A A的列向量(第 j j j列)
注意以下特殊类型的矩阵
- 同型矩阵:行数与列数对应相等
- 方阵:行数与列数相等
- 零矩阵 O O O
- 单位 E E E阵:是方阵,主对角线上的元素均为1。除此以外全都为0
- 对角阵:是方阵,只有主对角线上有元素。除此以外全都为0
- 对称阵:若 A = A T A=A^{T} A=AT,则称该矩阵为对称阵
(2)本质
- 可以发现,从图像上理解线性变换比较直观但是难以表达,那么究竟应该如何表达这种线性变换呢?
矩阵:矩阵是用来刻画变换的,它用数值来描述线性变换
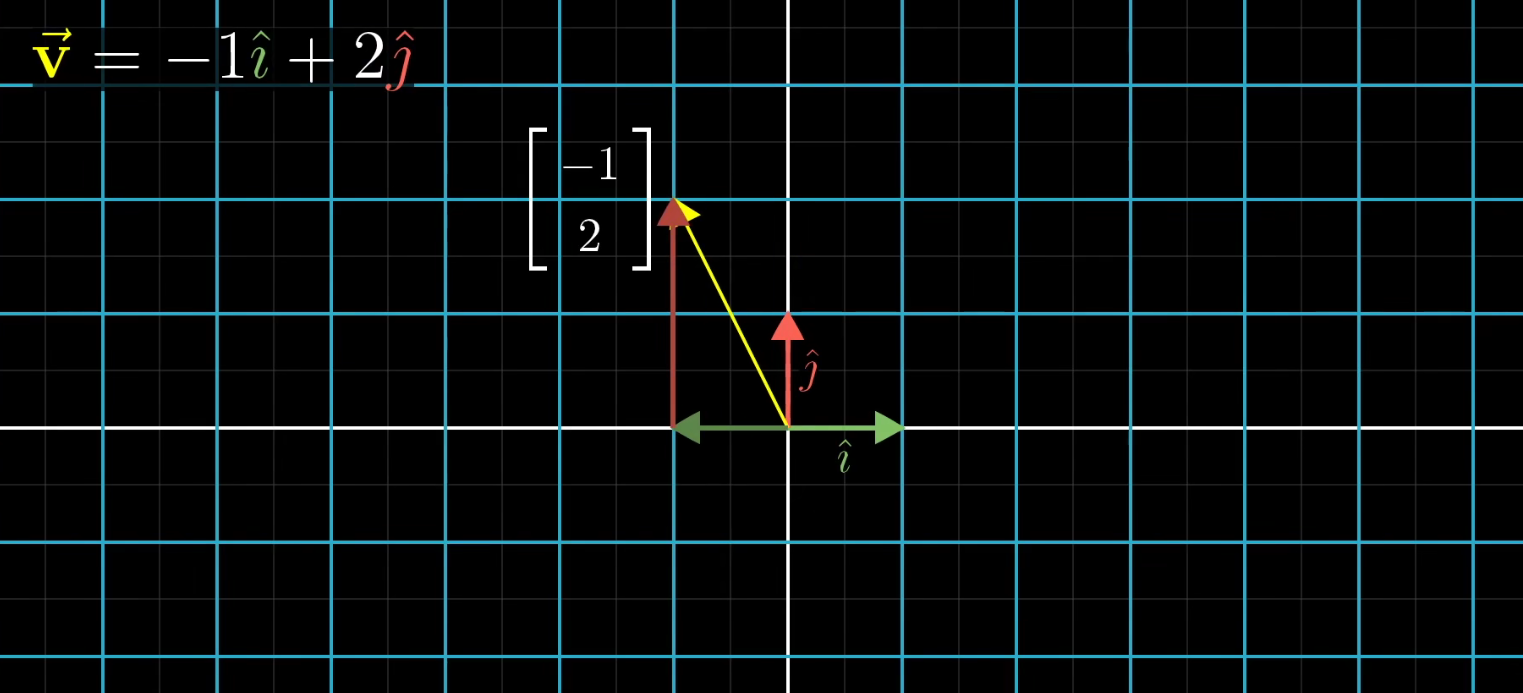
例如,现在有一个向量 ( − 1 2 ) \begin{pmatrix} -1\\ 2\end{pmatrix} (−12),它可以看做是基向量 i j ij ij的线性组合
施加一个线性变换
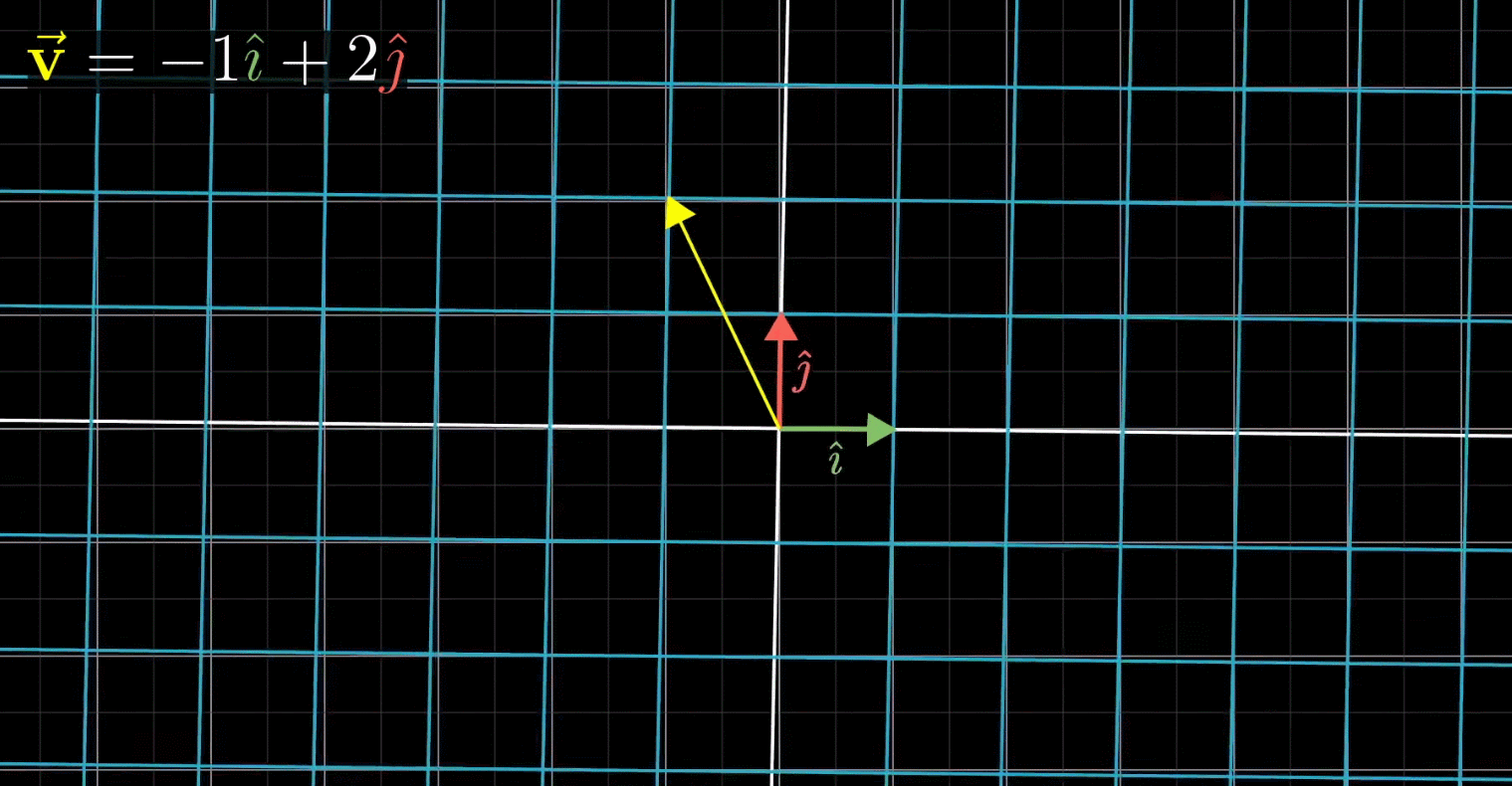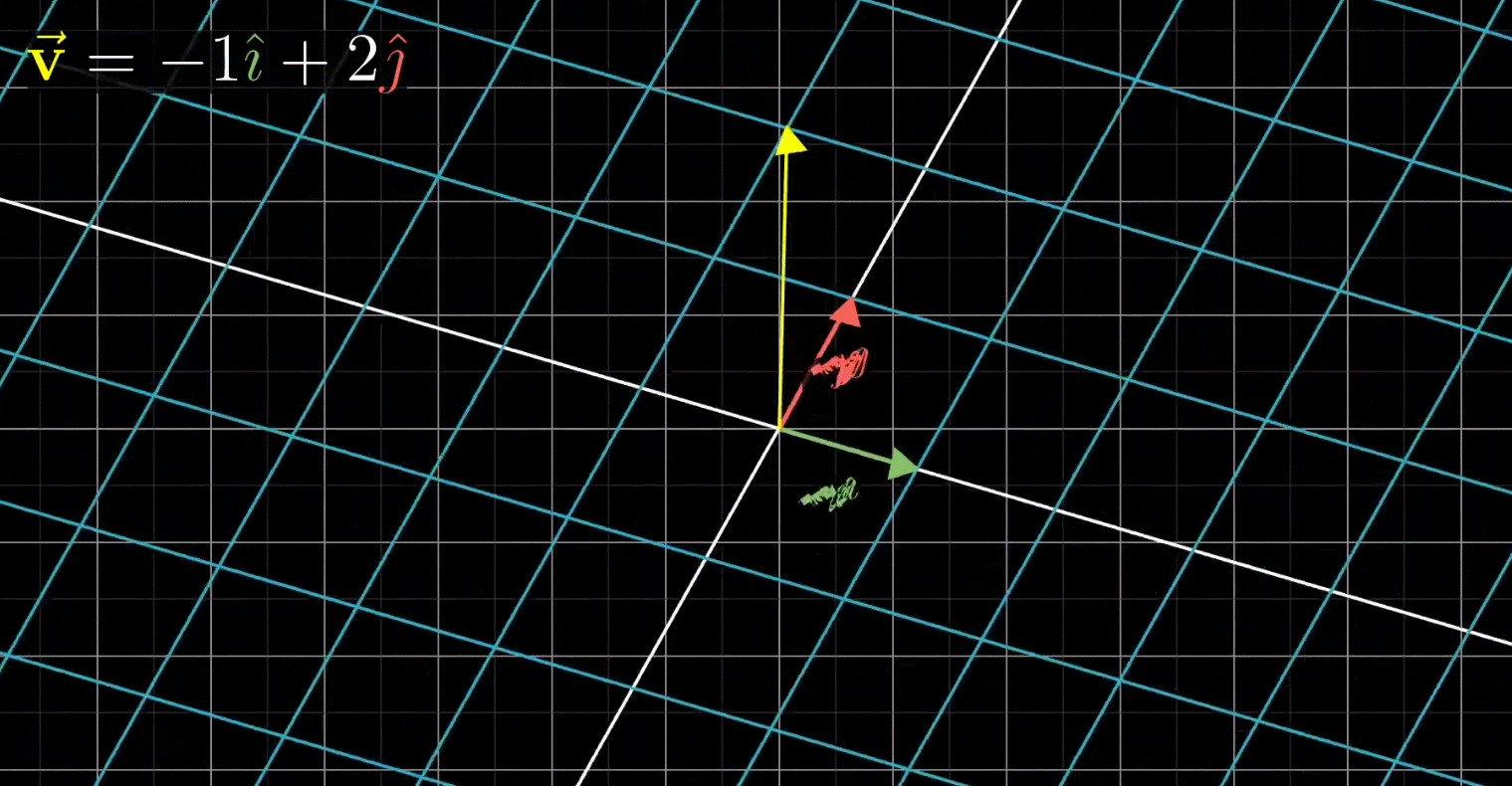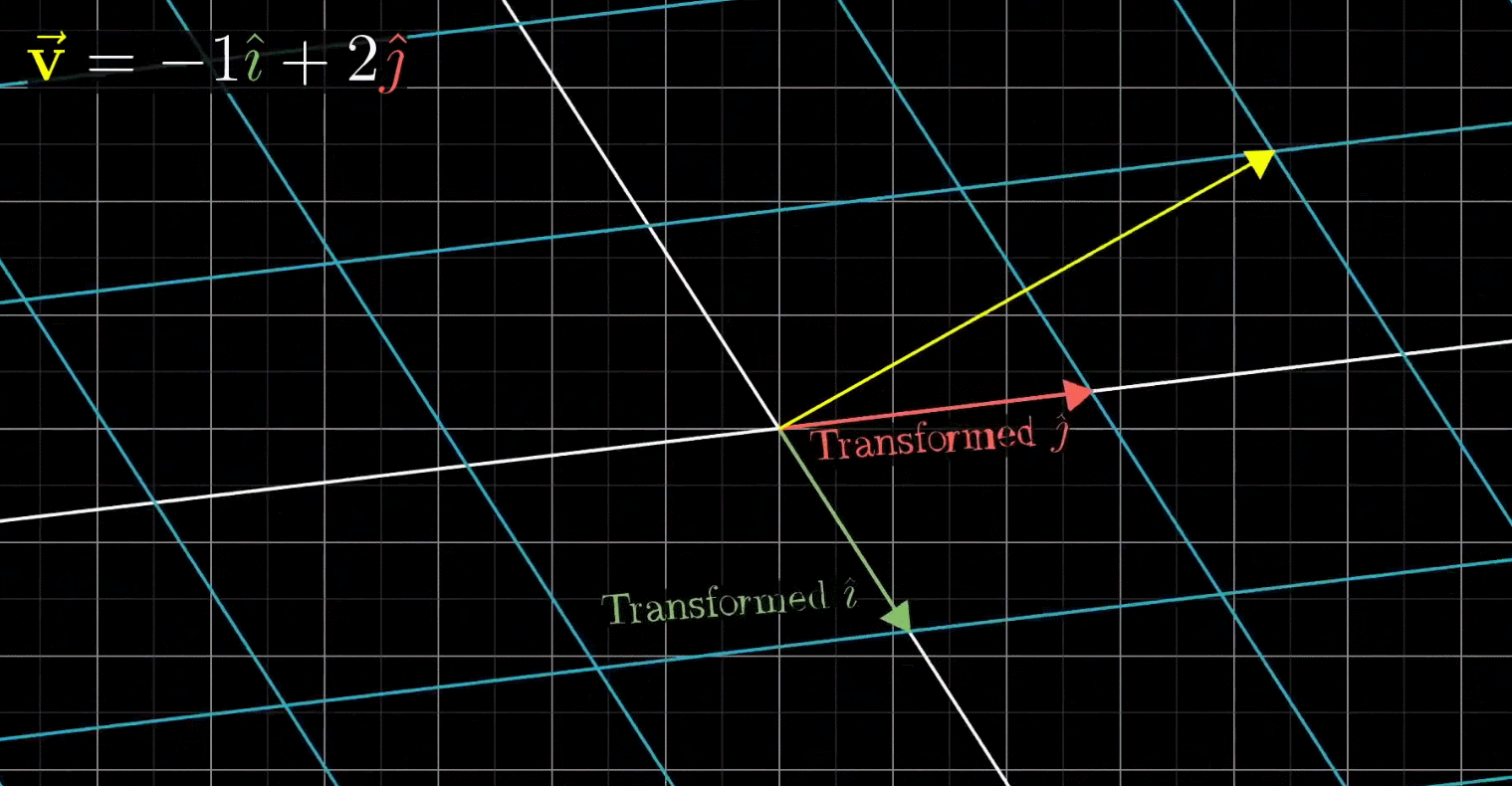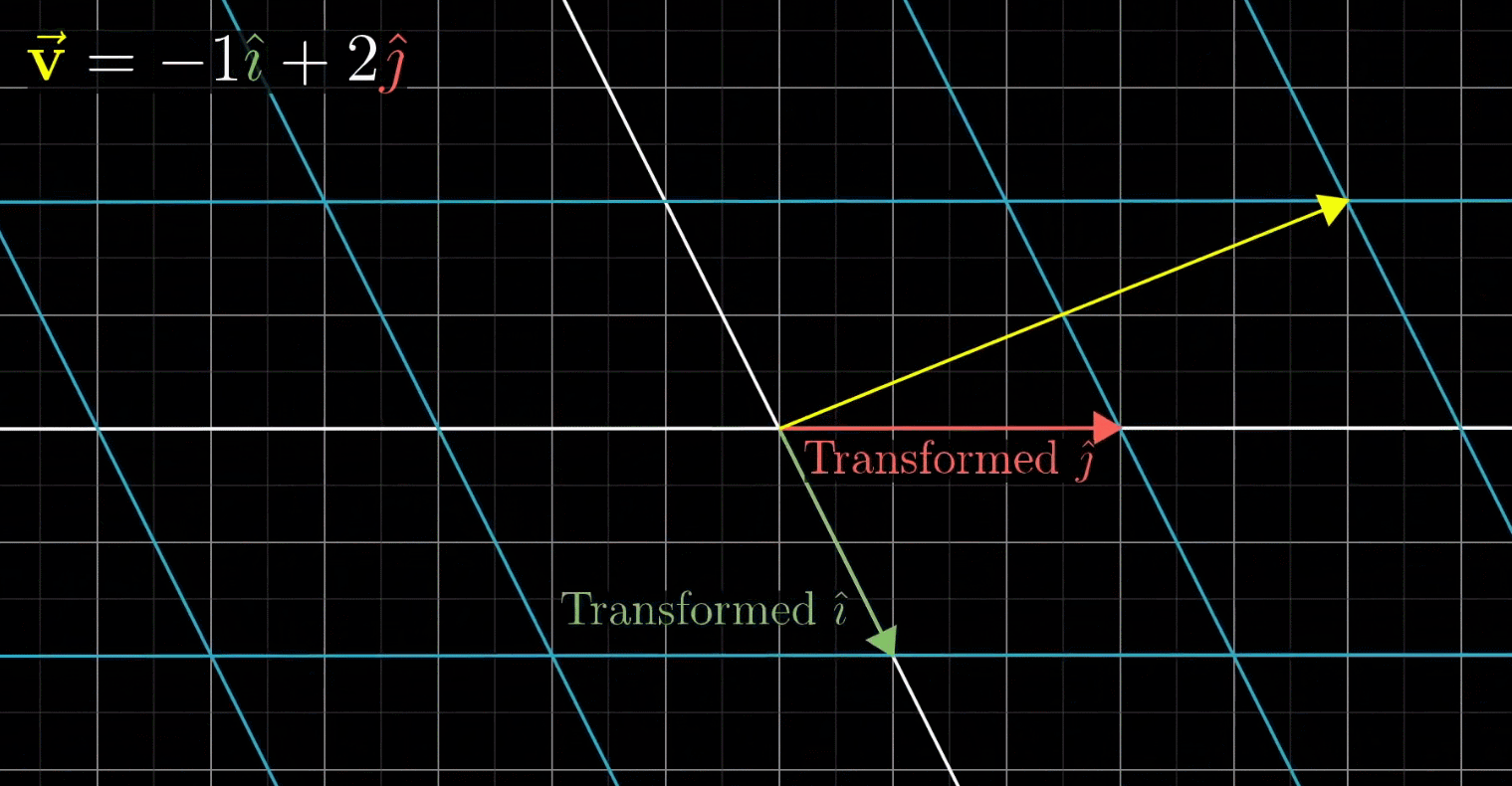
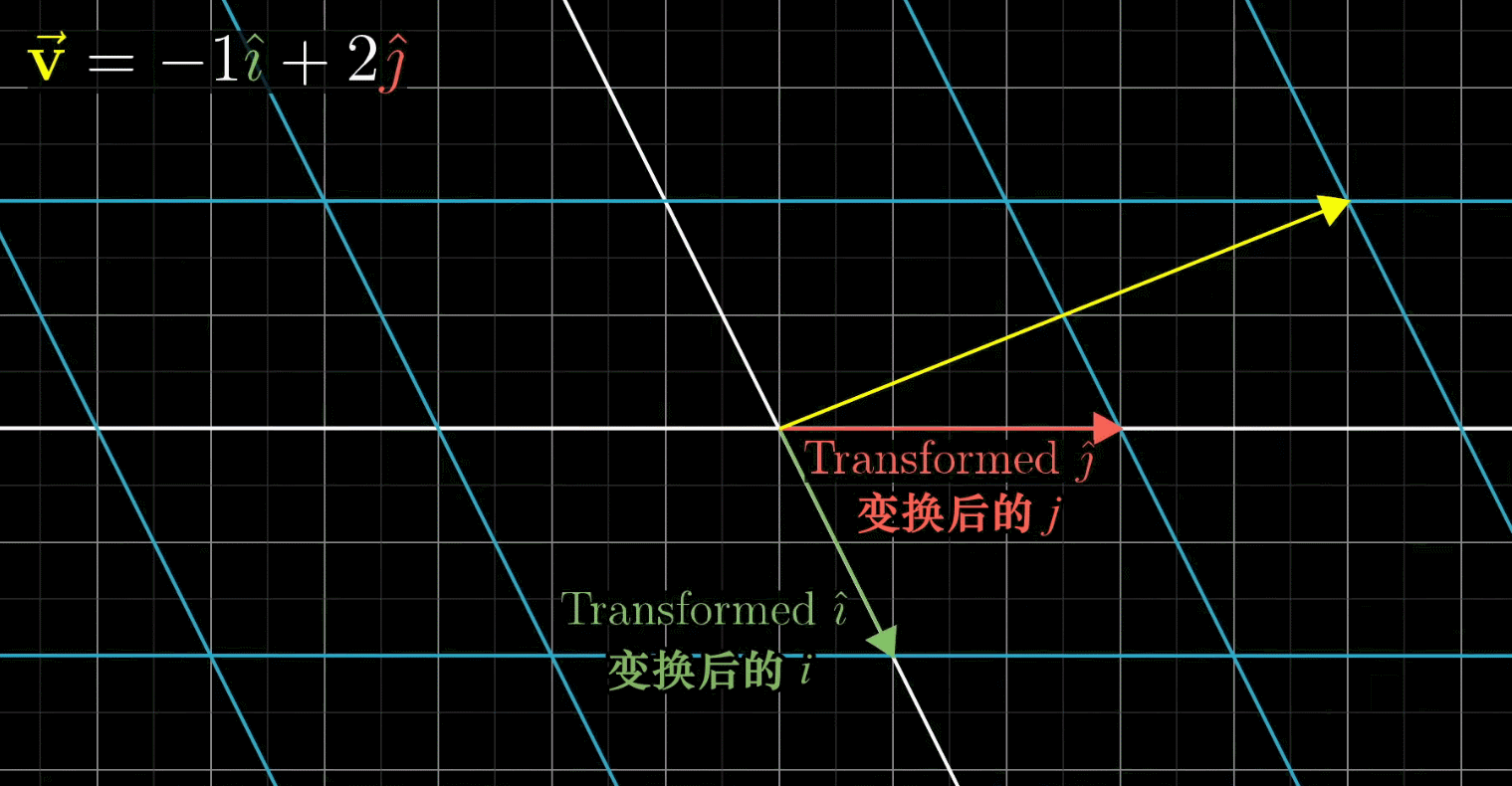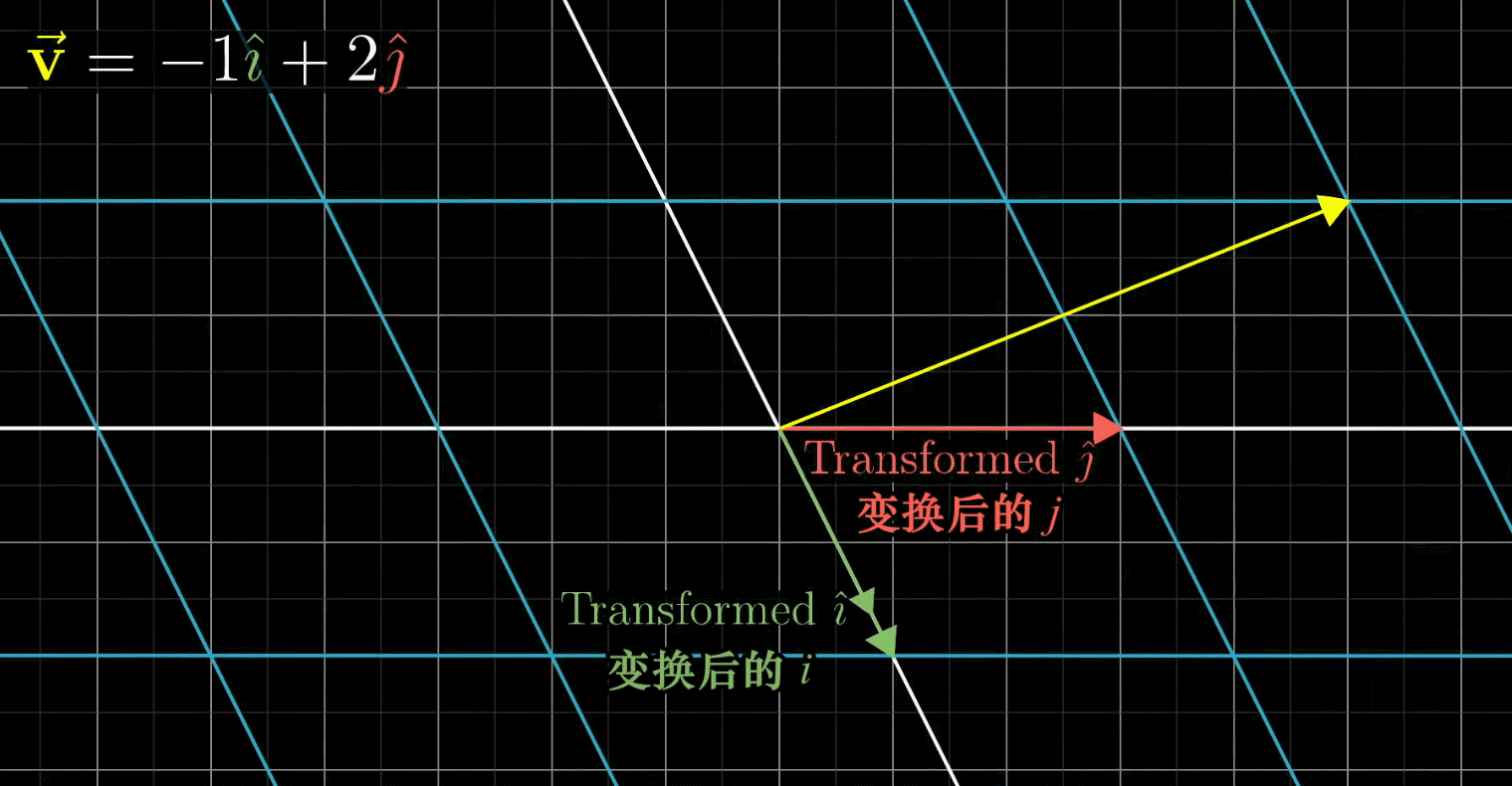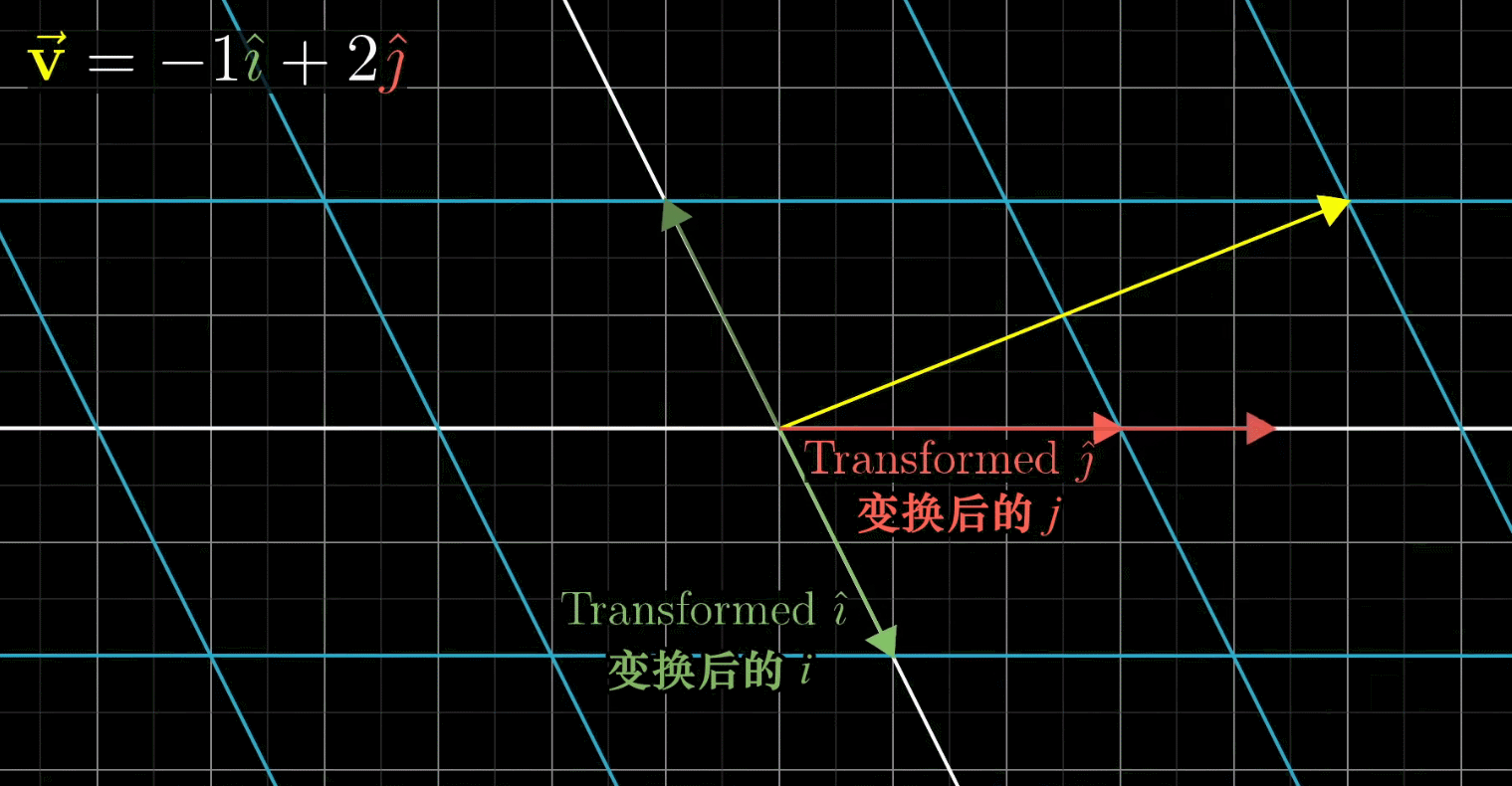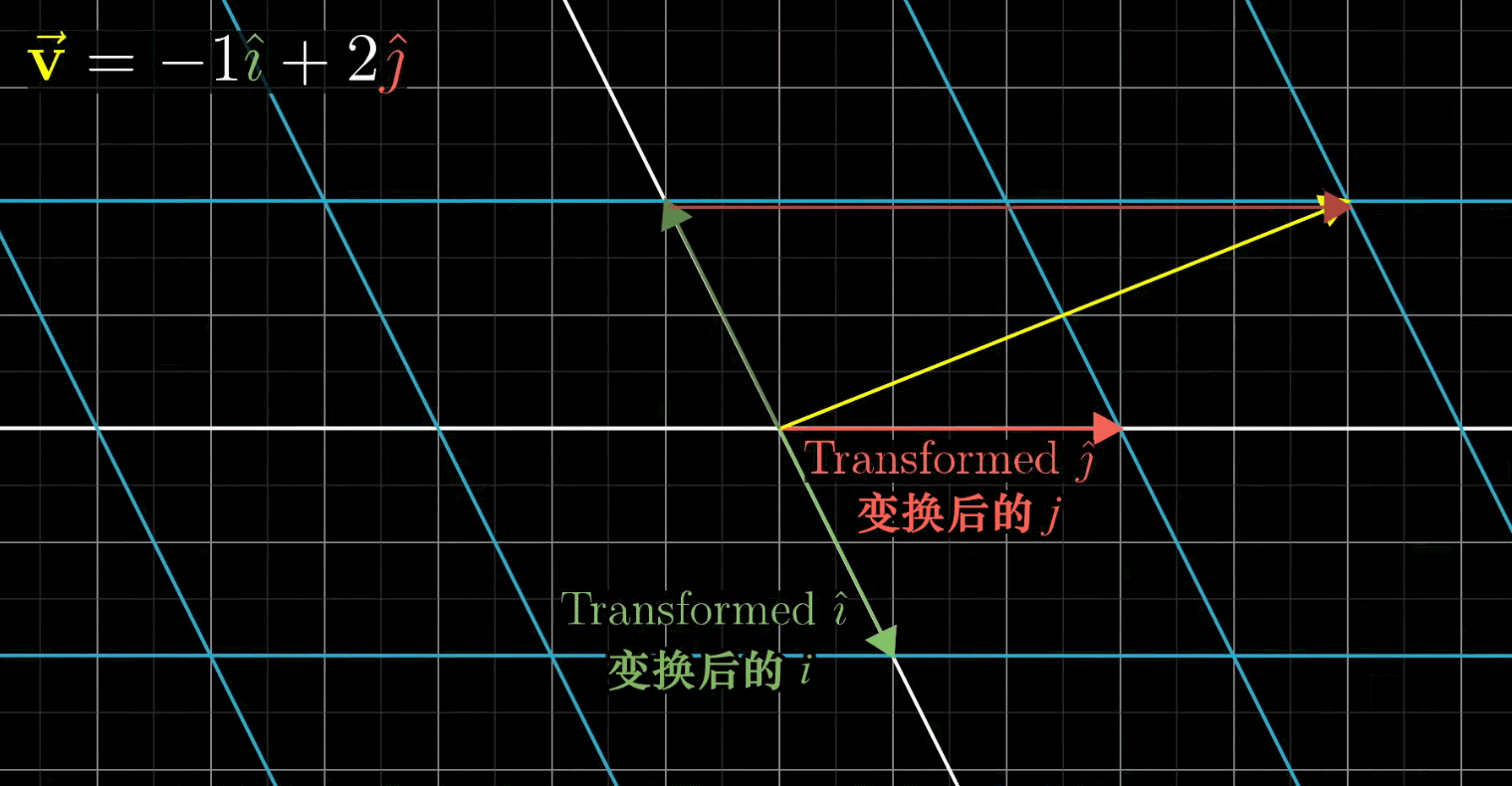
这里, v ‾ \overline v v和 i j ij ij都发生了变换,不再是以前的 v v v和 i j ij ij,由于线性变换会保证网格线平行且等距分布,所以变换后的 v v v的位置是-1与变换后 i i i之积+2与变换后 j j j之积
换句话说:既然 v ‾ \overline v v是 i j ij ij的特定的线性组合,那么变换后的 v ‾ \overline v v也是变换后的 i j ij ij的特定的线性组合。这意味着:你可以只根据变换后的 i j ij ij推断出变换后的 v ‾ \overline v v
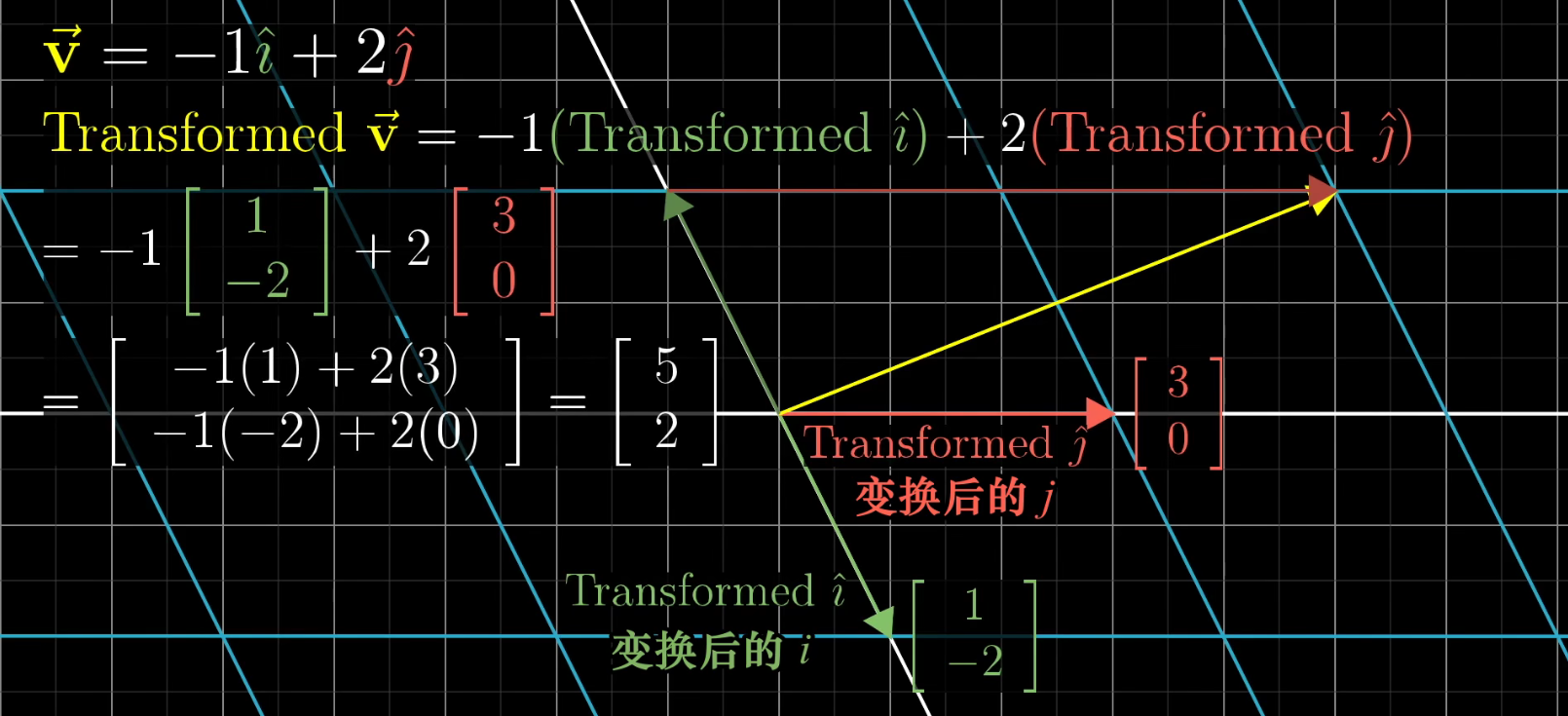
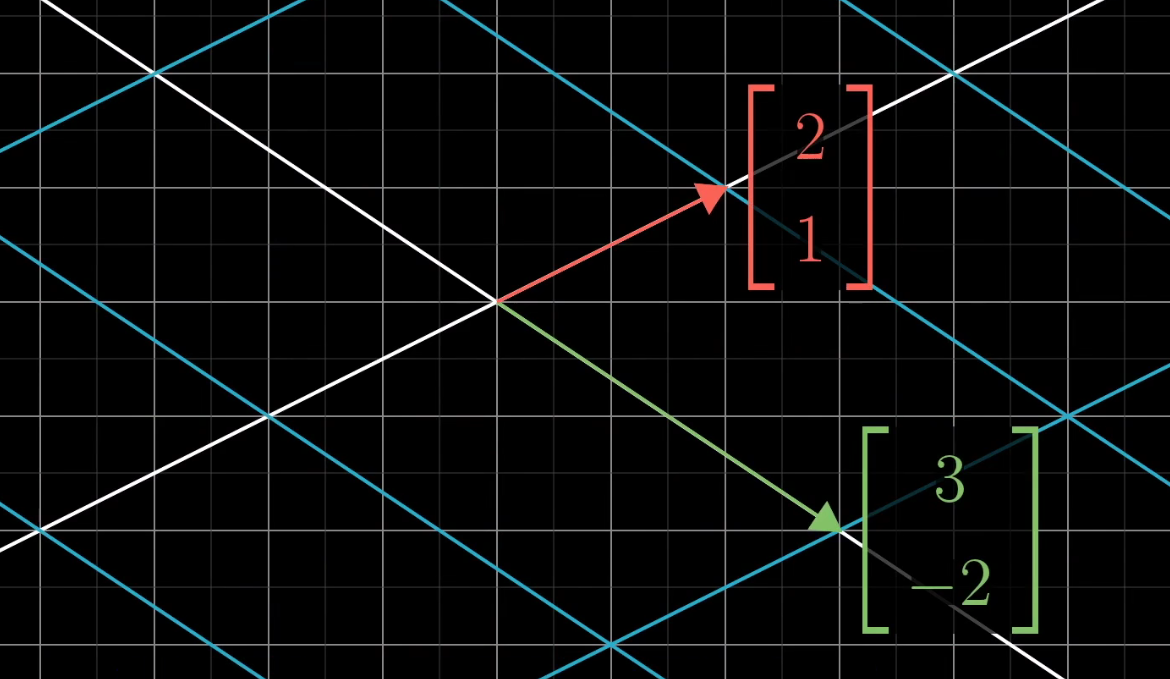
在上图所示的情形中,变换后的向量 i j ij ij分别为 ( 1 − 2 ) \begin{pmatrix} 1\\ -2\end{pmatrix} (1−2)和 ( 3 0 ) \begin{pmatrix} 3\\ 0\end{pmatrix} (30),于是,变换后的 v ‾ \overline v v=-1 ( 1 − 2 ) \begin{pmatrix} 1\\ -2\end{pmatrix} (1−2)+2 ( 3 0 ) \begin{pmatrix} 3\\ 0\end{pmatrix} (30)= ( − 1 ( 1 ) + 2 ( 3 ) − 1 ( − 2 ) + 2 ( 0 ) ) \begin{pmatrix} -1(1)+2(3)\\ -1(-2)+2(0)\end{pmatrix} (−1(1)+2(3)−1(−2)+2(0))= ( 5 2 ) \begin{pmatrix} 5\\ 2\end{pmatrix} (52),于是变换后的 v ‾ \overline v v一定落在 ( 5 2 ) \begin{pmatrix} 5\\ 2\end{pmatrix} (52)处
因此只要记录了变换后的 i j ij ij,我们就可以推断出任意向量在变换后的位置,而不必观察变换本身是怎样的
一般情况下,假如一个向量的坐标是 ( x y ) \begin{pmatrix} x\\ y\end{pmatrix} (xy),变换后的这个向量就是 x x x乘以变换后的 i i i,也即 ( 1 − 2 ) \begin{pmatrix} 1\\ -2\end{pmatrix} (1−2)加上 y y y乘以变换后的 j j j,也即 ( 3 0 ) \begin{pmatrix} 3\\ 0\end{pmatrix} (30),因此它将会落在 ( 1 x + 3 y − 2 x + 0 y ) \begin{pmatrix} 1x+3y\\ -2x+0y\end{pmatrix} (1x+3y−2x+0y)位置处
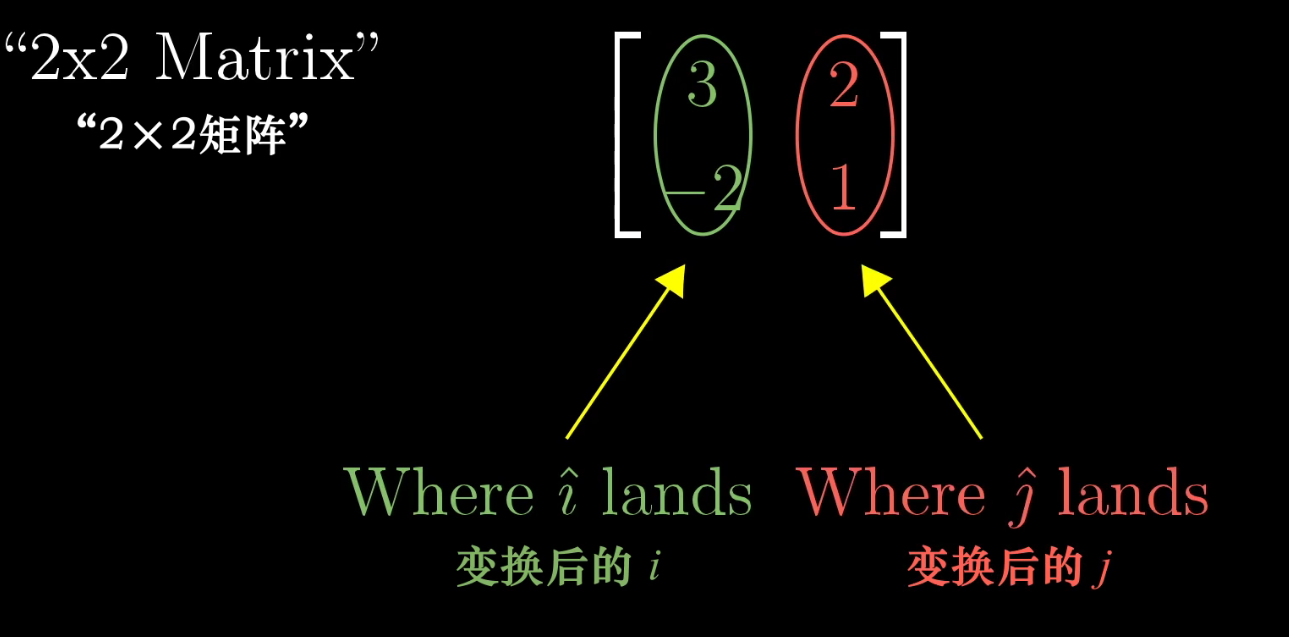
综上,一个二维线性变换仅由四个数字完全确定,也即变换后的 i i i的 ( x , y ) (x,y) (x,y)和变换后的 j j j的 ( x , y ) (x,y) (x,y)
通常我们将这些坐标包装在一个2×2的格子中,称其为矩阵(2×2阶),矩阵只是一个记号,它描述了线性变换的信息
如果你有一个描述线性变化的2×2阶矩阵,以及一个给定的向量,你想了解线性变化对这个向量的作用,你只需取出向量的坐标,将它们分别与矩阵特定的列相乘,然后结果相加即可
考虑一般的矩阵 ( a b c d ) \begin{pmatrix} a & b\\ c & d\end{pmatrix} (acbd),把第一列 ( a c ) \begin{pmatrix} a\\ c\end{pmatrix} (ac)看作变换后的第一个基向量,把第二列 ( b d ) \begin{pmatrix} b\\ d\end{pmatrix} (bd)看作变换后的第二个基向量,让此变换作用于一个向量 ( x y ) \begin{pmatrix} x\\ y\end{pmatrix} (xy),就会得到 ( a x + b y c x + d y ) \begin{pmatrix} ax+by\\ cx+dy\end{pmatrix} (ax+bycx+dy),这便是矩阵乘法的定义
三:矩阵运算
(1)矩阵的线性运算
A:加法
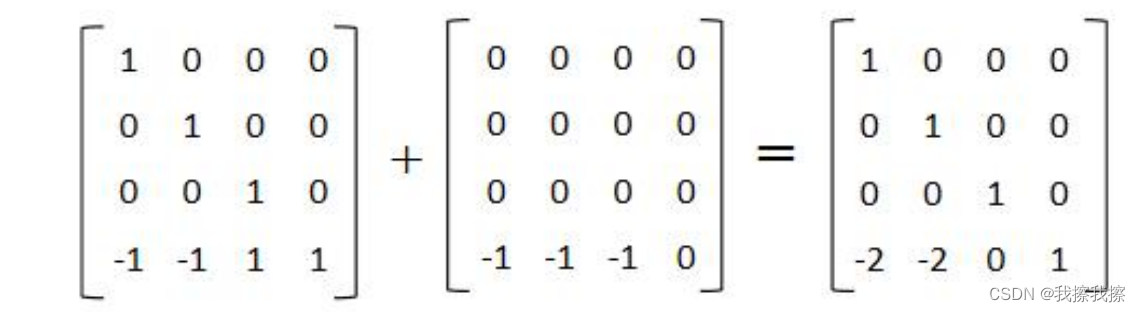
矩阵加法:只有同型矩阵才能进行加法运算,矩阵相加时对应元素相加即可
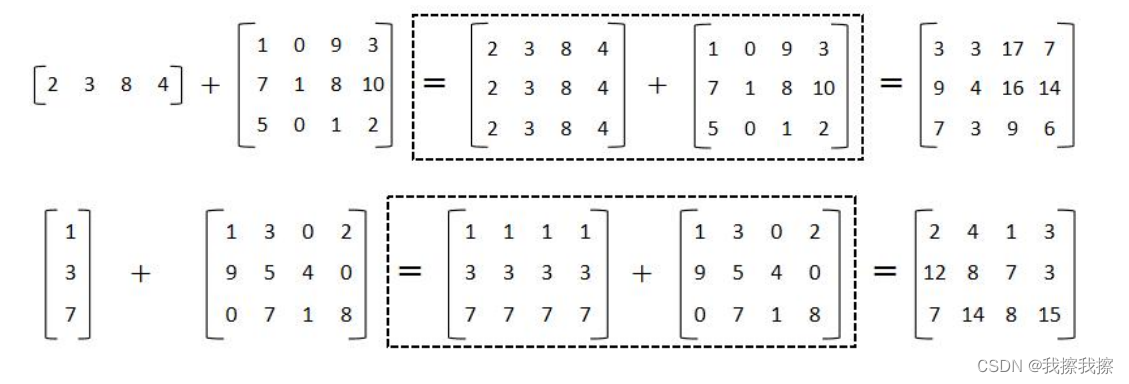
向量与矩阵相加时需要把向量补全为相应矩阵才可以进行
矩阵加法满足结合律和交换律
B:数乘
数乘:
(2)矩阵乘法
A:概念
矩阵乘法:矩阵 A A A、 B B B的乘积 A B AB AB,其实是矩阵 A A A的各个行向量与矩阵 B B B的各个列向量进行内积运算后组成的新矩阵
B:本质
- 矩阵用于描述变换,但我们前面所讲到的变化都是一种单一的变化,如果你想描述多种连续的变换,就可以使用复合变换
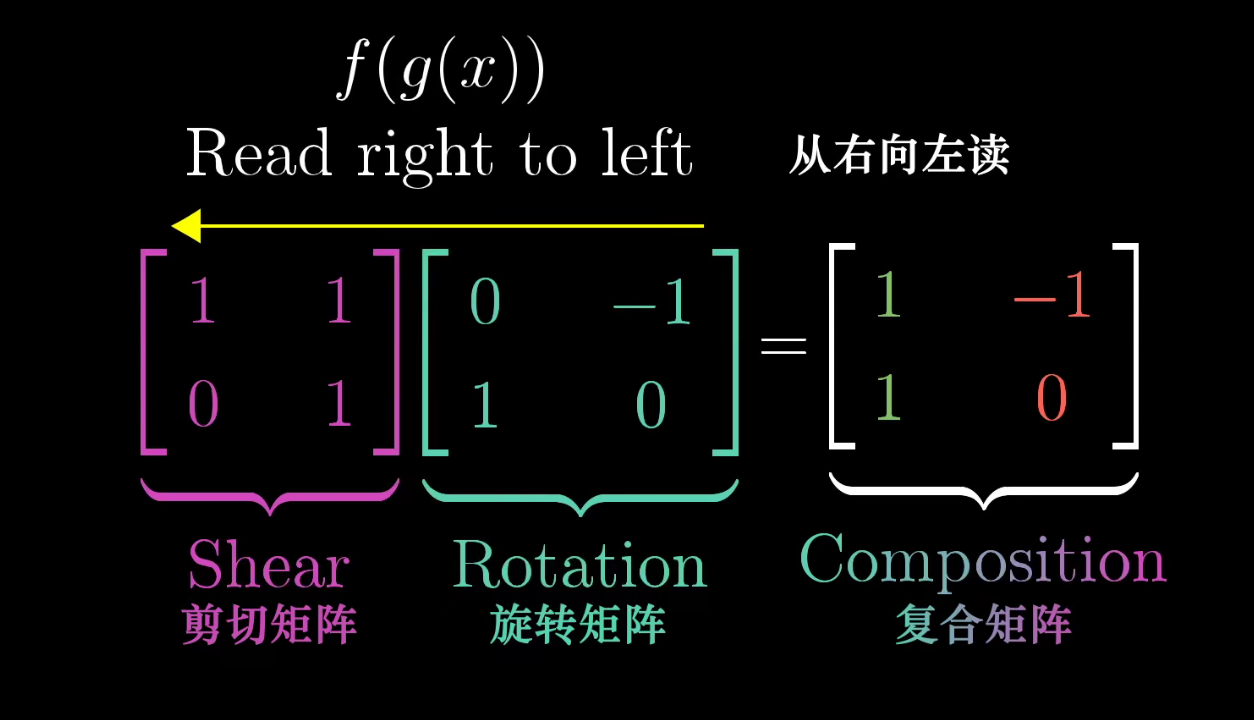
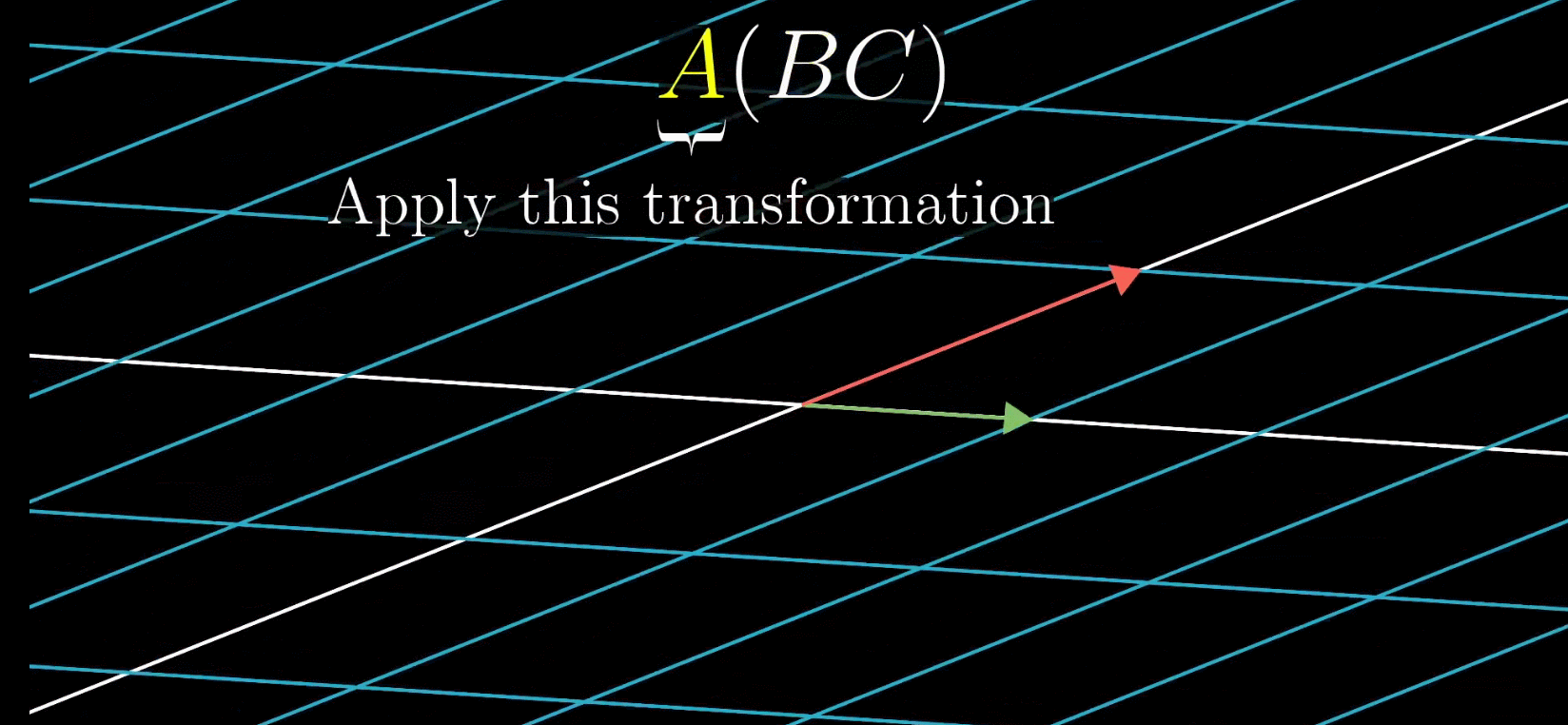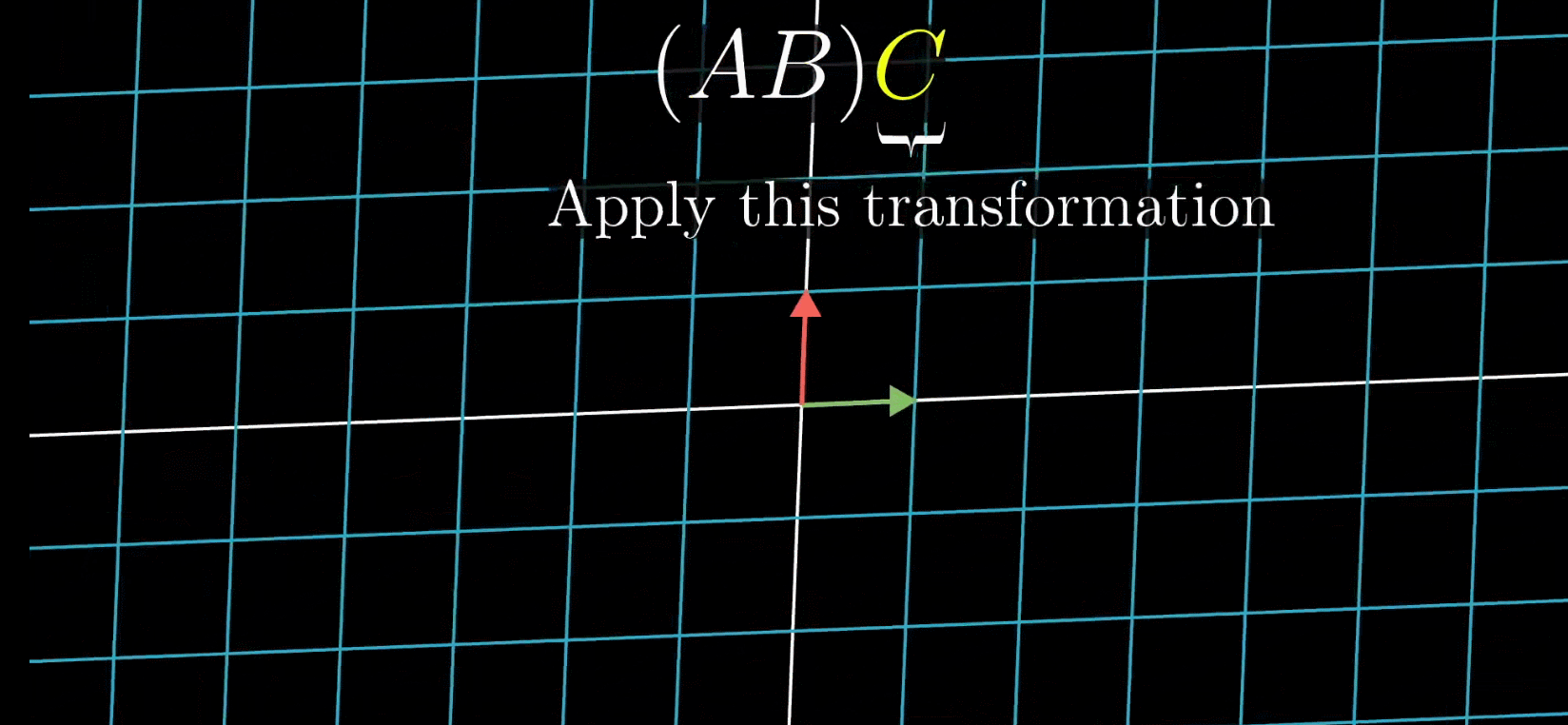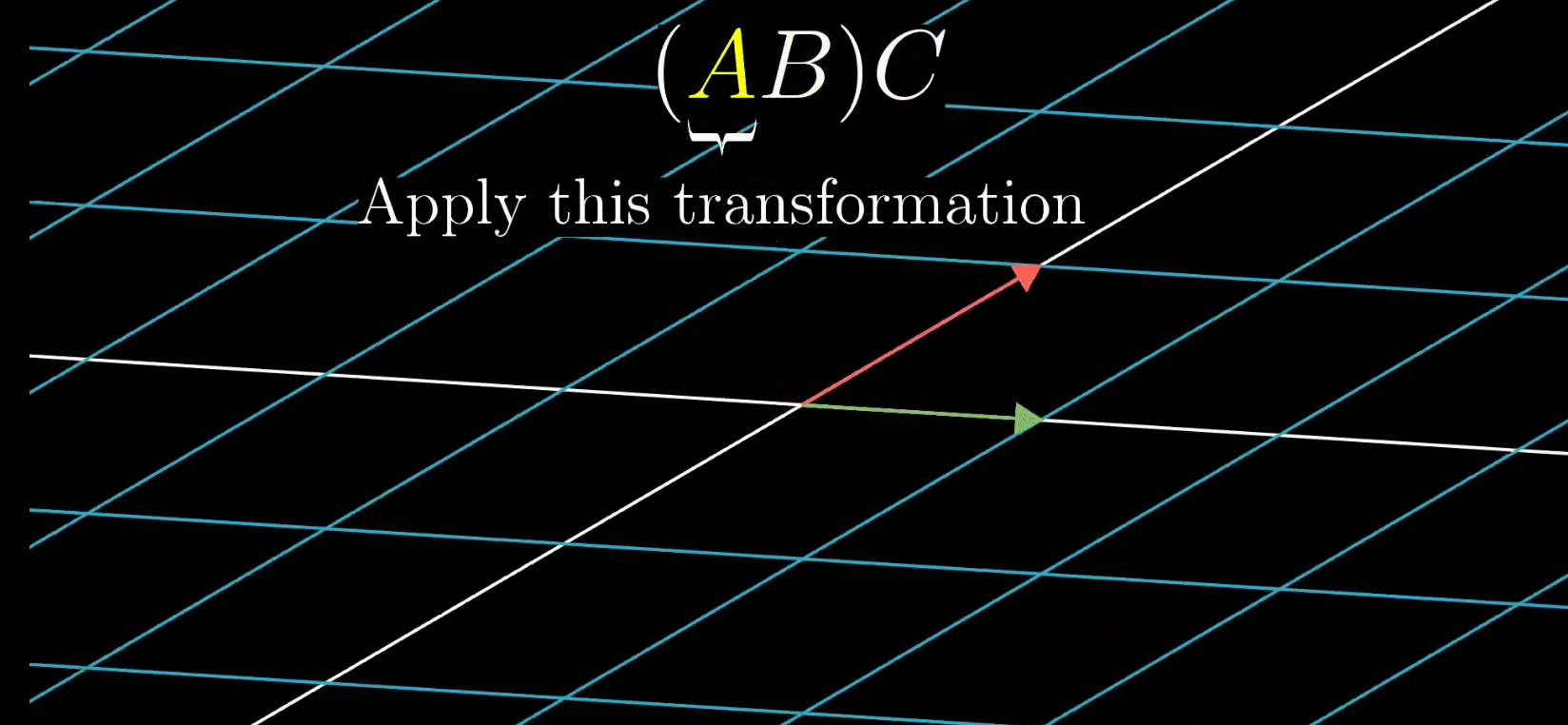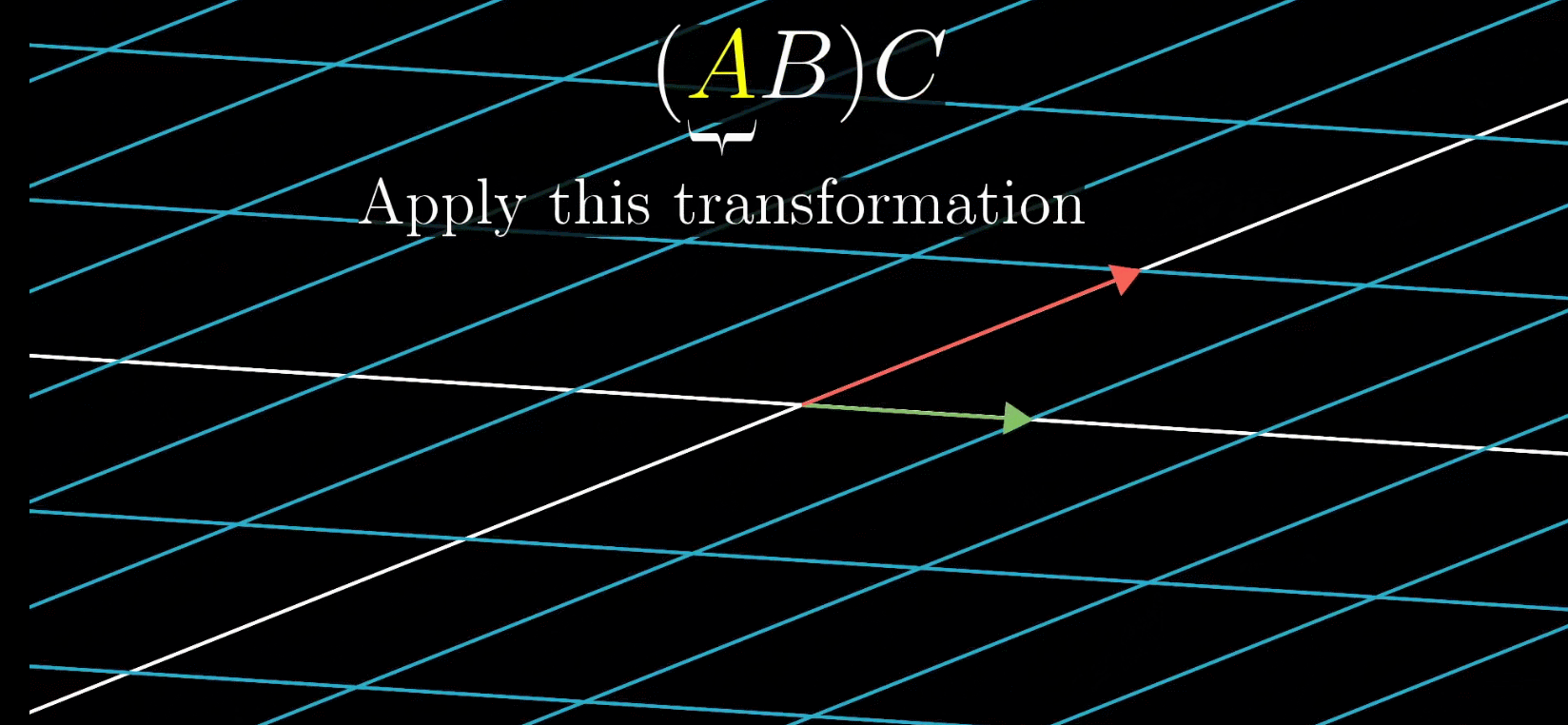
如下图,先将平面逆时针旋转90°,然后再进行剪切。很明显,这是两个变换,但我们可以把它复合为一个变换,即旋转和剪切作用的总和,他们对应的矩阵分别为 ( 1 1 1 0 ) \begin{pmatrix} 1 & 1\\ 1 & 0\end{pmatrix} (1110)和 ( 0 − 1 1 0 ) \begin{pmatrix} 0 & -1\\ 1 & 0\end{pmatrix} (01−10)
经过旋转和剪切后,最终变化对应矩阵表示为 ( 1 − 1 1 0 ) \begin{pmatrix} 1 & -1\\ 1 & 0\end{pmatrix} (11−10)
所以对于一个向量 ( x y ) \begin{pmatrix} x\\ y\end{pmatrix} (xy),我们先对其施加旋转,再对其施加剪切,用乘法描述就是下面这样
( 1 1 1 0 ) ( ( 0 − 1 1 0 ) ( x y ) ) \begin{pmatrix} 1 & 1\\ 1 & 0\end{pmatrix}(\begin{pmatrix} 0 & -1\\ 1 & 0\end{pmatrix}\begin{pmatrix} x\\ y\end{pmatrix}) (1110)((01−10)(xy))
而从总体效果上看,就是对向量 ( x y ) \begin{pmatrix} x\\ y\end{pmatrix} (xy)施加以符合变化,即
( 1 − 1 1 0 ) ( x y ) \begin{pmatrix} 1 & -1\\ 1 & 0\end{pmatrix}\begin{pmatrix} x\\ y\end{pmatrix} (11−10)(xy)
联立两个等式
( 1 1 1 0 ) ( ( 0 − 1 1 0 ) ( x y ) ) = ( 1 − 1 1 0 ) ( x y ) \begin{pmatrix} 1 & 1\\ 1 & 0\end{pmatrix}(\begin{pmatrix} 0 & -1\\ 1 & 0\end{pmatrix}\begin{pmatrix} x\\ y\end{pmatrix})=\begin{pmatrix} 1 & -1\\ 1 & 0\end{pmatrix}\begin{pmatrix} x\\ y\end{pmatrix} (1110)((01−10)(xy))=(11−10)(xy)
约去等式相同部分,那么两者之积理应是相同的
( 1 1 1 0 ) ( 0 − 1 1 0 ) = ( 1 − 1 1 0 ) \begin{pmatrix} 1 & 1\\ 1 & 0\end{pmatrix}\begin{pmatrix} 0 & -1\\ 1 & 0\end{pmatrix}=\begin{pmatrix} 1 & -1\\ 1 & 0\end{pmatrix} (1110)(01−10)=(11−10)
这两个矩阵的作用是需要从右往左看的,如下图,可以理解为先 M 1 M_{1} M1后 M 2 M_{2} M2,矩阵 M 2 M_{2} M2= ( 1 1 0 1 ) \begin{pmatrix} 1 & 1\\ 0 & 1\end{pmatrix} (1011)作用于 M 1 M_{1} M1的第一列得到 ( 1 1 ) \begin{pmatrix} 1\\ 1\end{pmatrix} (11),同样矩阵 M 2 M_{2} M2= ( 1 1 0 1 ) \begin{pmatrix} 1 & 1\\ 0 & 1\end{pmatrix} (1011)作用于 M 1 M_{1} M1的第二列得到 ( − 1 0 ) \begin{pmatrix} -1\\ 0\end{pmatrix} (−10)
在实际计算会用一种普适性的方法计算出结果矩阵,这边是我们熟知的矩阵乘法
- 我们的数学教育中太过重视怎么算的问题,但是怎么算有那么重要吗,上述一个简单的例子不就已经把矩阵乘法运算规则讲清楚了吗?我们的大脑负责的是抽象,而运算的东西交给计算机就行。所以大家一定要明白矩阵乘法的本质,而不应该迷失在数字的世界中无法自拔
( a b c d ) ( e f g h ) = ( a e + b g a f + b h c e + d g c f + d h ) \begin{pmatrix} a & b\\ c & d\end{pmatrix}\begin{pmatrix} e & f\\ g & h\end{pmatrix}=\begin{pmatrix} ae+bg & af+bh\\ ce+dg& cf+dh\end{pmatrix} (acbd)(egfh)=(ae+bgce+dgaf+bhcf+dh)
C:关于矩阵乘法的两个问题
①:矩阵乘法为什么不满足交换律
- 你当然可以通过代数运算证明 A B = B A AB=BA AB=BA,但这是没有任何意义的,所以我们还是需要通过变换的角度理解
仍然使用上面的例子,这次先剪切再选择,也即 M 1 M 2 M_{1}M_{2} M1M2,那么最终效果如下。可以发现这与之前的变换根本不是同一个,所以矩阵乘法不能交换,变换是有顺序的,乘法自然也是也必须满足一定顺序
②:矩阵乘法为什么满足结合律
- A B C = A ( B C ) = ( A B ) C ABC = A(BC) = (AB)C ABC=A(BC)=(AB)C
在这种情况下无论你先计算AB然后再计算ABC,还是先计算BC然后再计算ABC,最终的变换效果是一致的,那么自然而然是满足结合律的
D:矩阵的幂
- A k A l = A k + l A^{k}A^{l}=A^{k+l} AkAl=Ak+l
- ( A B ) T = B T A T (AB)^{T}=B^{T}A^{T} (AB)T=BTAT
- ( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1} (AB)−1=B−1A−1
- ( A B ) k ≠ A k B k (AB)^{k}\neq A^{k}B^{k} (AB)k=AkBk
E:Hadamard积(基本积)
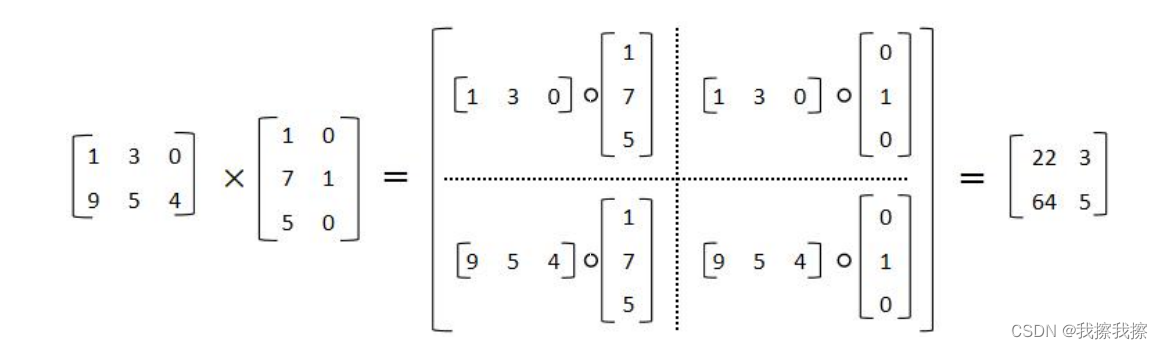
Hadamard积(基本积):若 A A A、 B B B是两个同阶矩阵,元素分别为 a i j a_{ij} aij和 b i j b_{ij} bij,若矩阵 C C C中每个元素 c i j = a i j × b i j c_{ij}=a_{ij}×b_{ij} cij=aij×bij,则称矩阵 C C C为矩阵 A A A和 B B B的Hadamard积(基本积)
C = A ○ B C=A ○B C=A○B
三:列相关矩阵
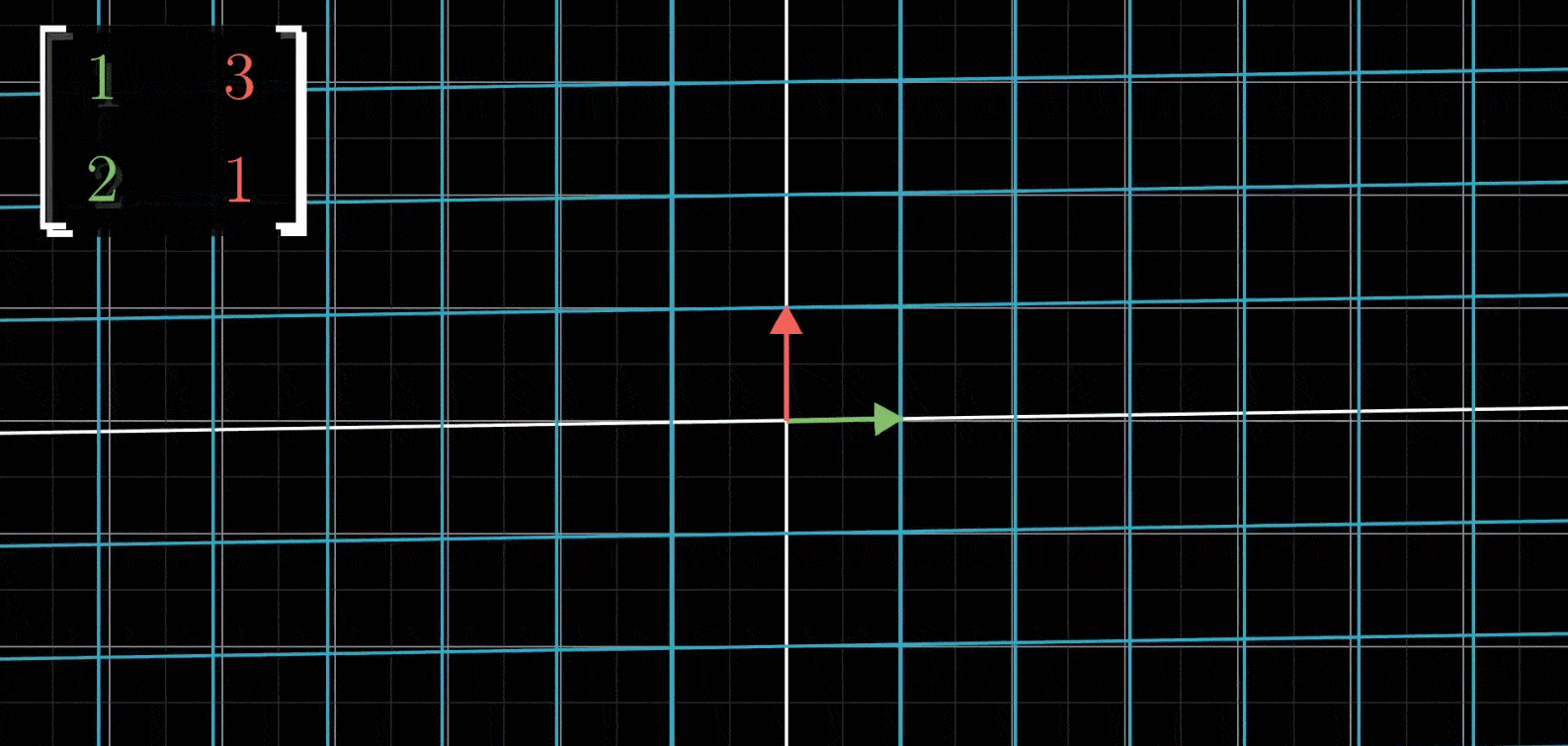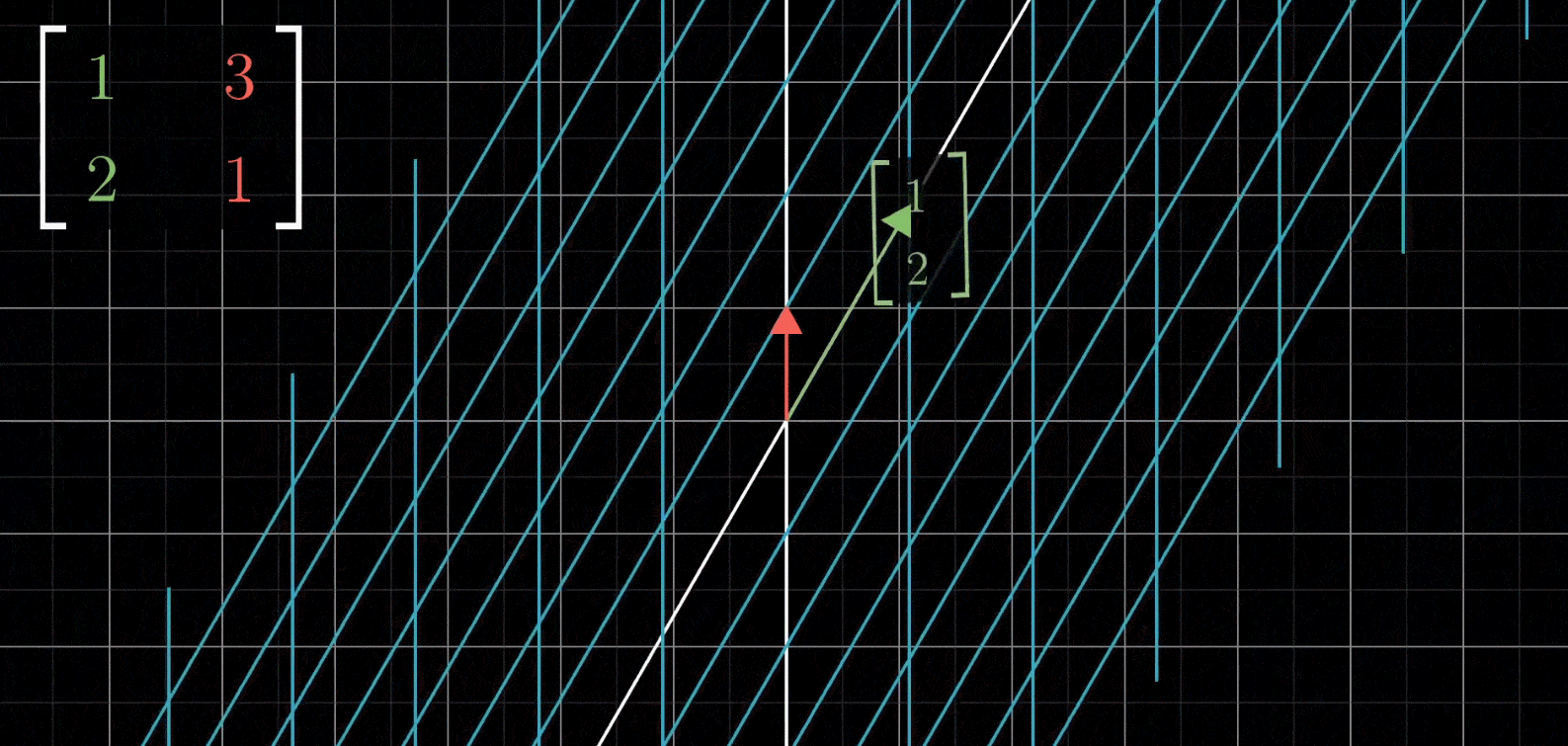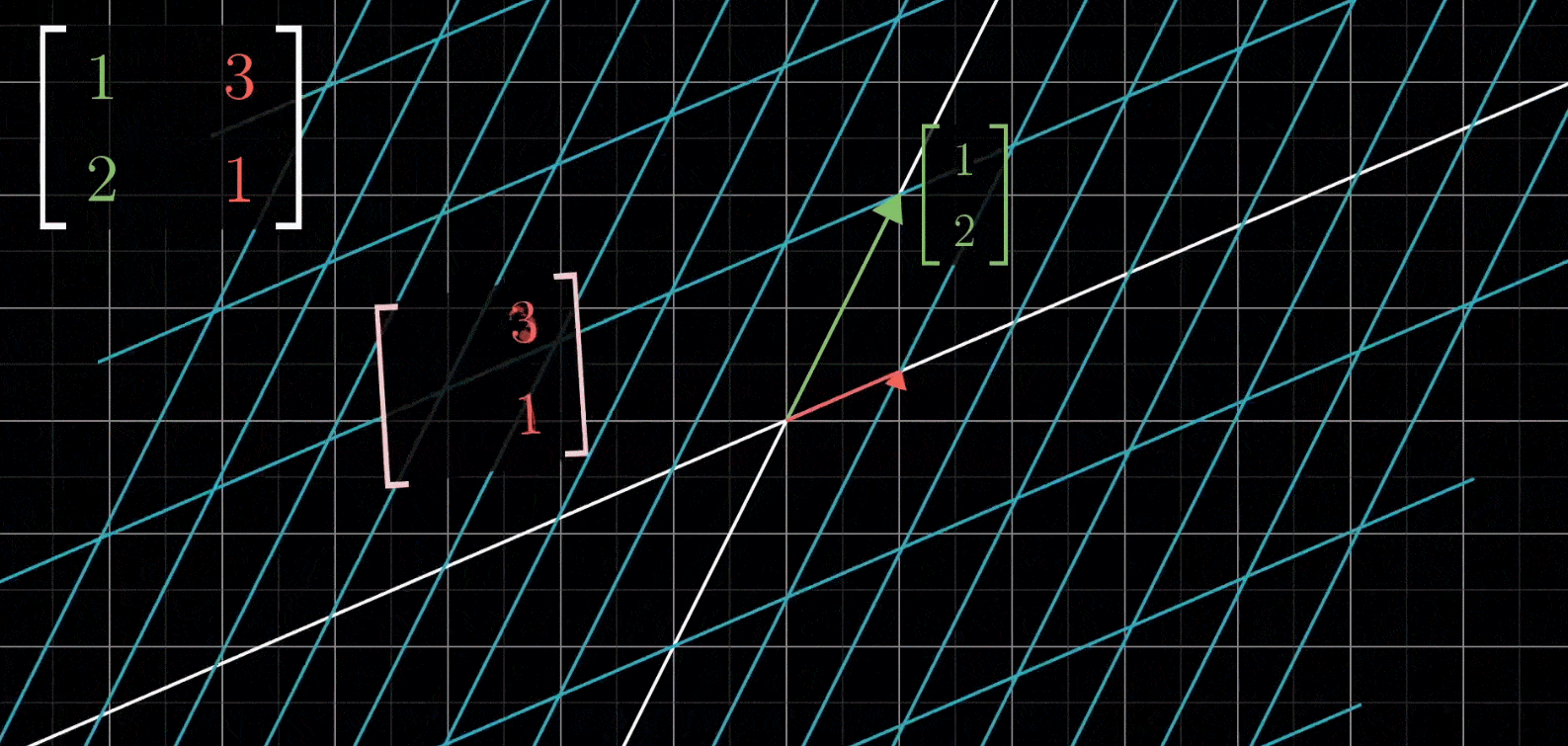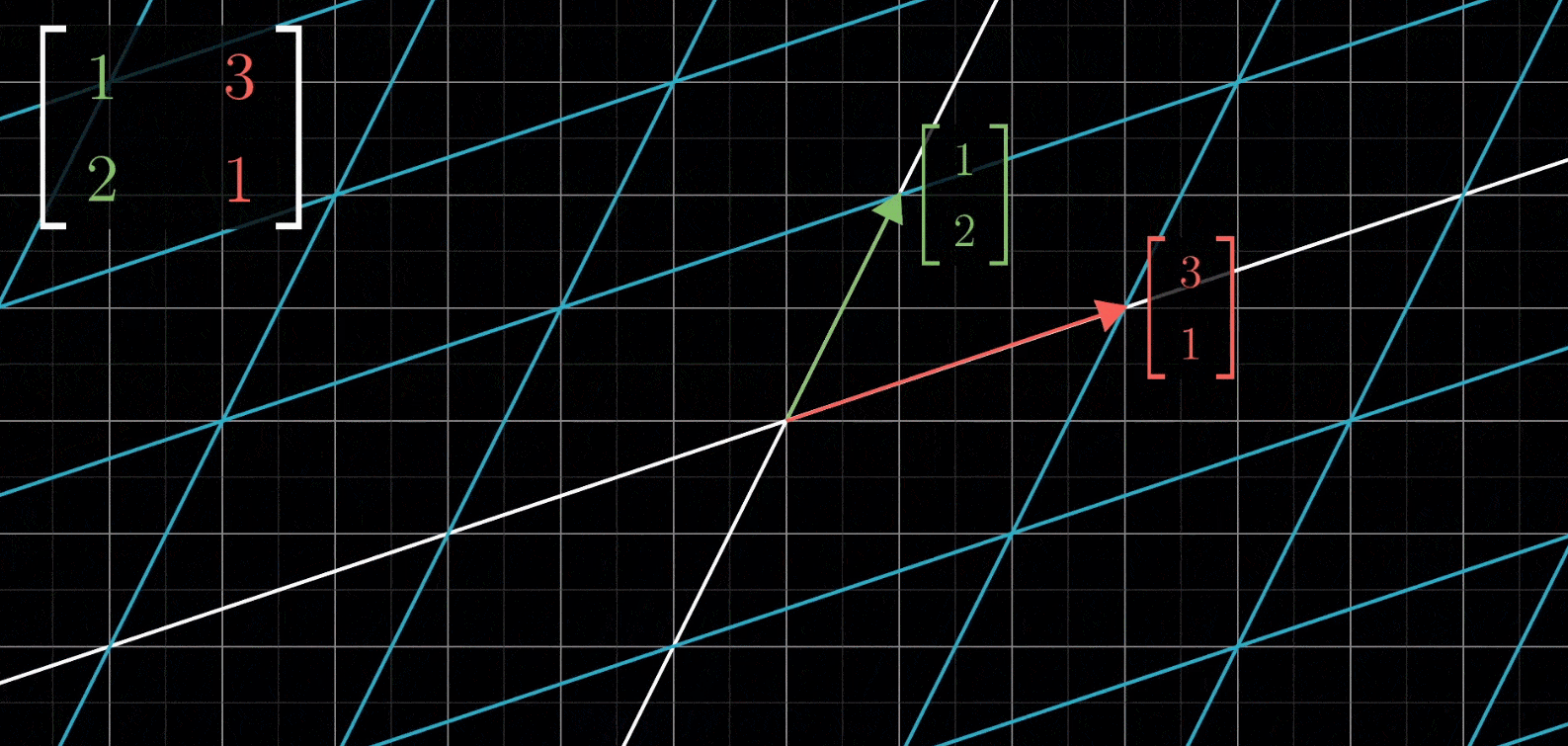
如果给出一个矩阵 ( 1 3 2 1 ) \begin{pmatrix} 1 & 3\\ 2 & 1\end{pmatrix} (1231),你能想象出来它的线性变换是怎么样的吗?
- 首先将 i i i移动到 ( 1 2 ) \begin{pmatrix} 1\\ 2\end{pmatrix} (12),然后将 j j j移动到 ( 3 1 ) \begin{pmatrix} 3\\ 1\end{pmatrix} (31),空间剩余部分随二者移动,保持网格线平行且等距分布
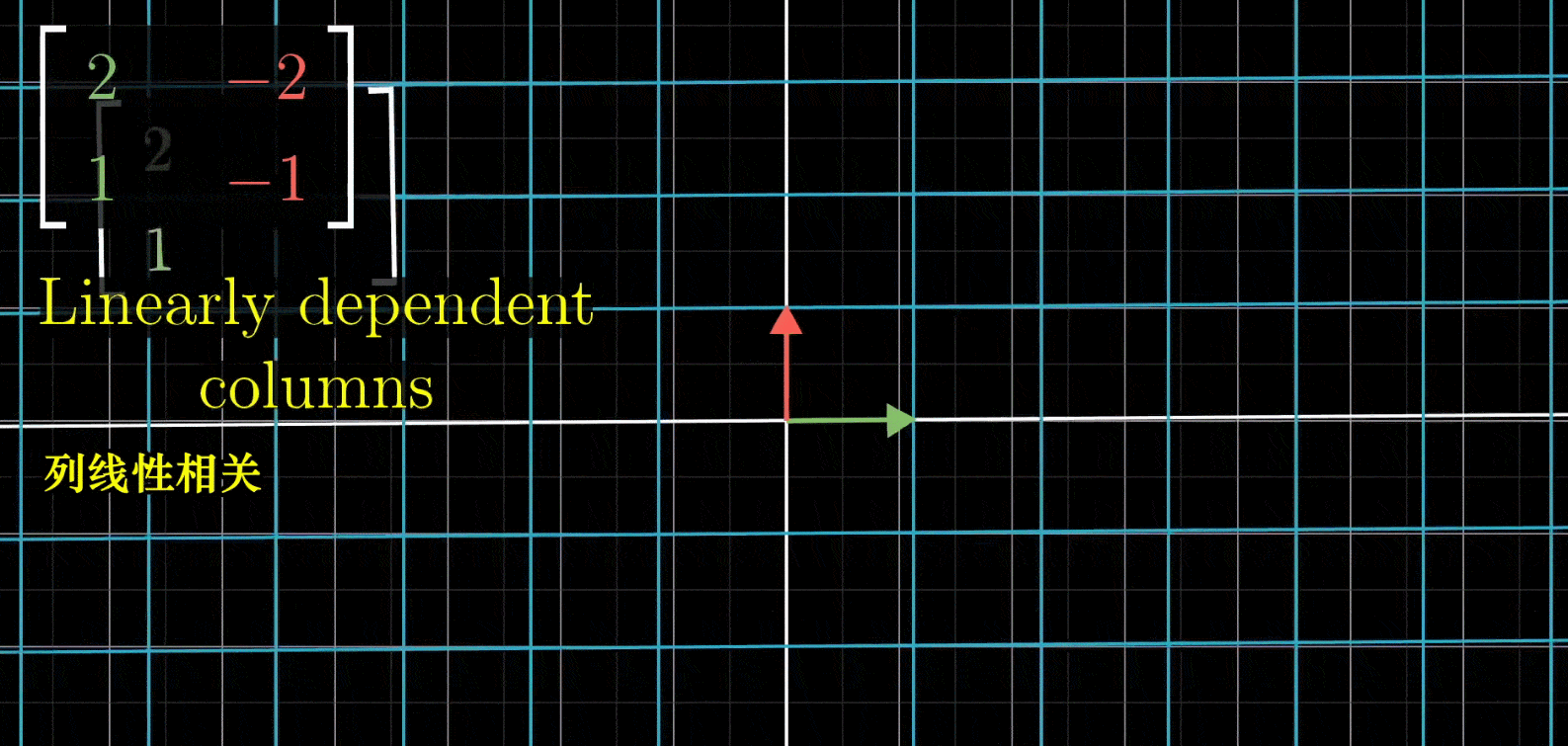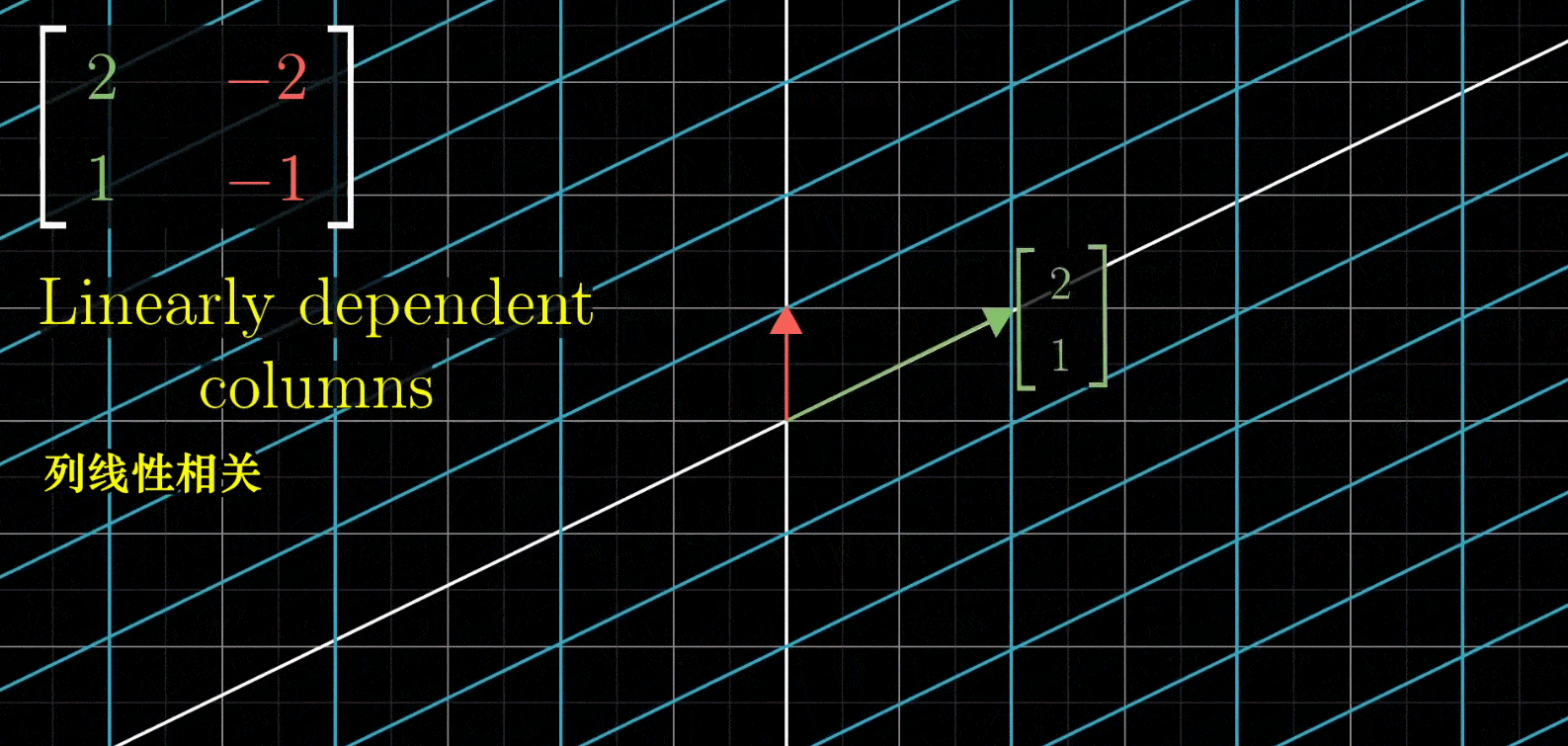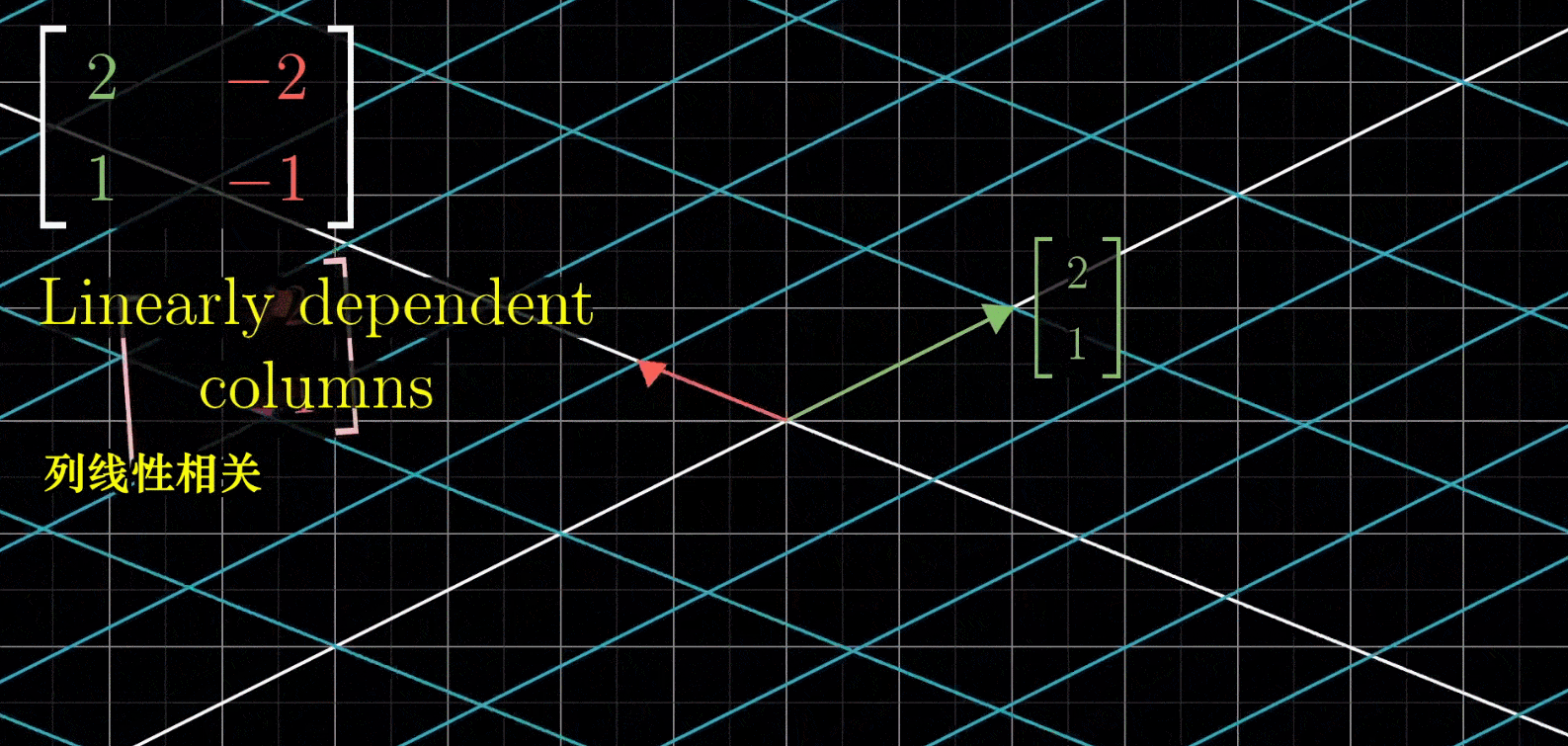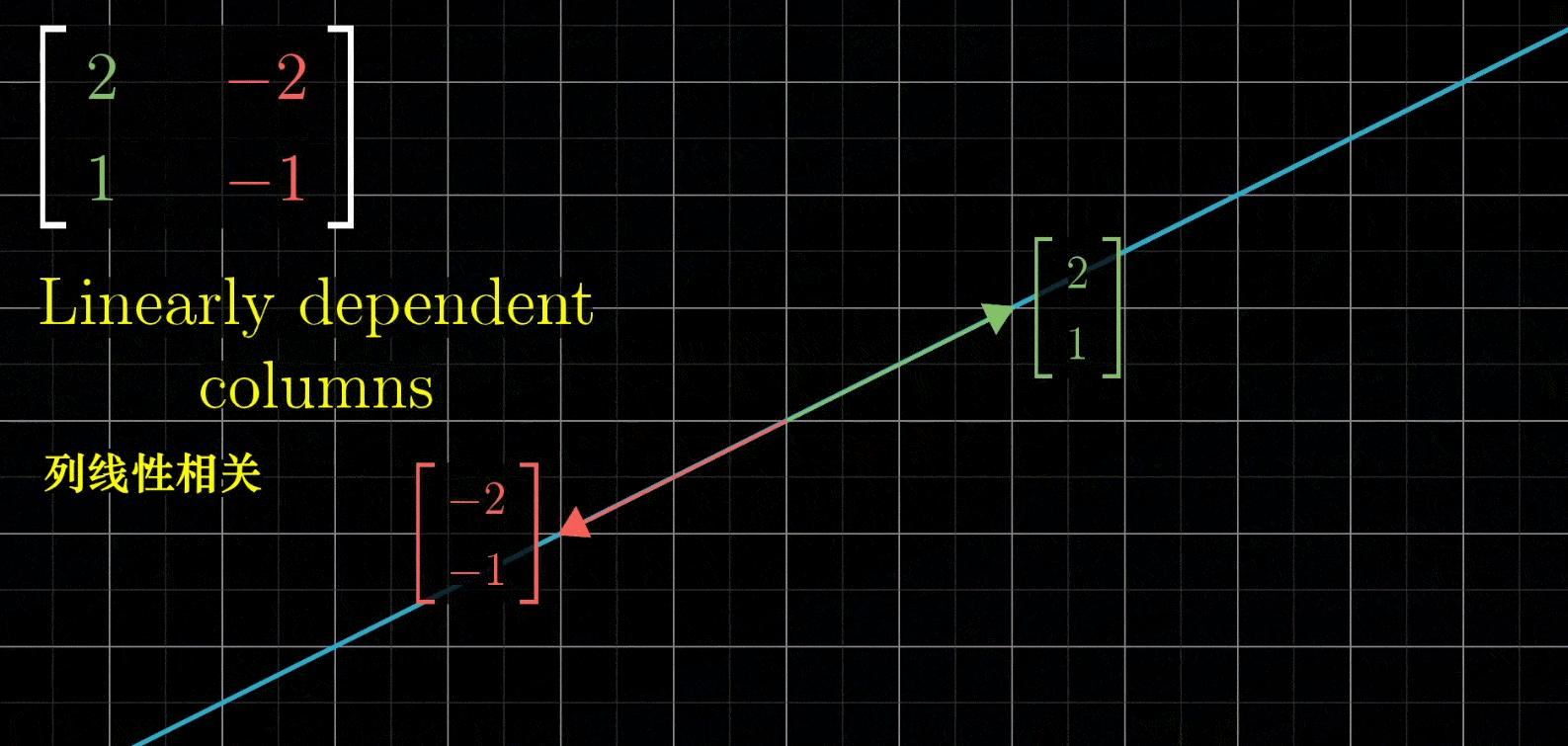
上面是一种普通情况,如果给出一个列相关的矩阵(意味着呈倍数关系), ( 2 − 2 1 − 1 ) \begin{pmatrix} 2 & -2\\ 1 & -1\end{pmatrix} (21−2−1),那么这样的线性变换会将整个二维空间全部挤压在他们所在的一条直线上
今天的文章
特征矩阵和特征向量的关系_特征向量求出来和答案不一样分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/81097.html