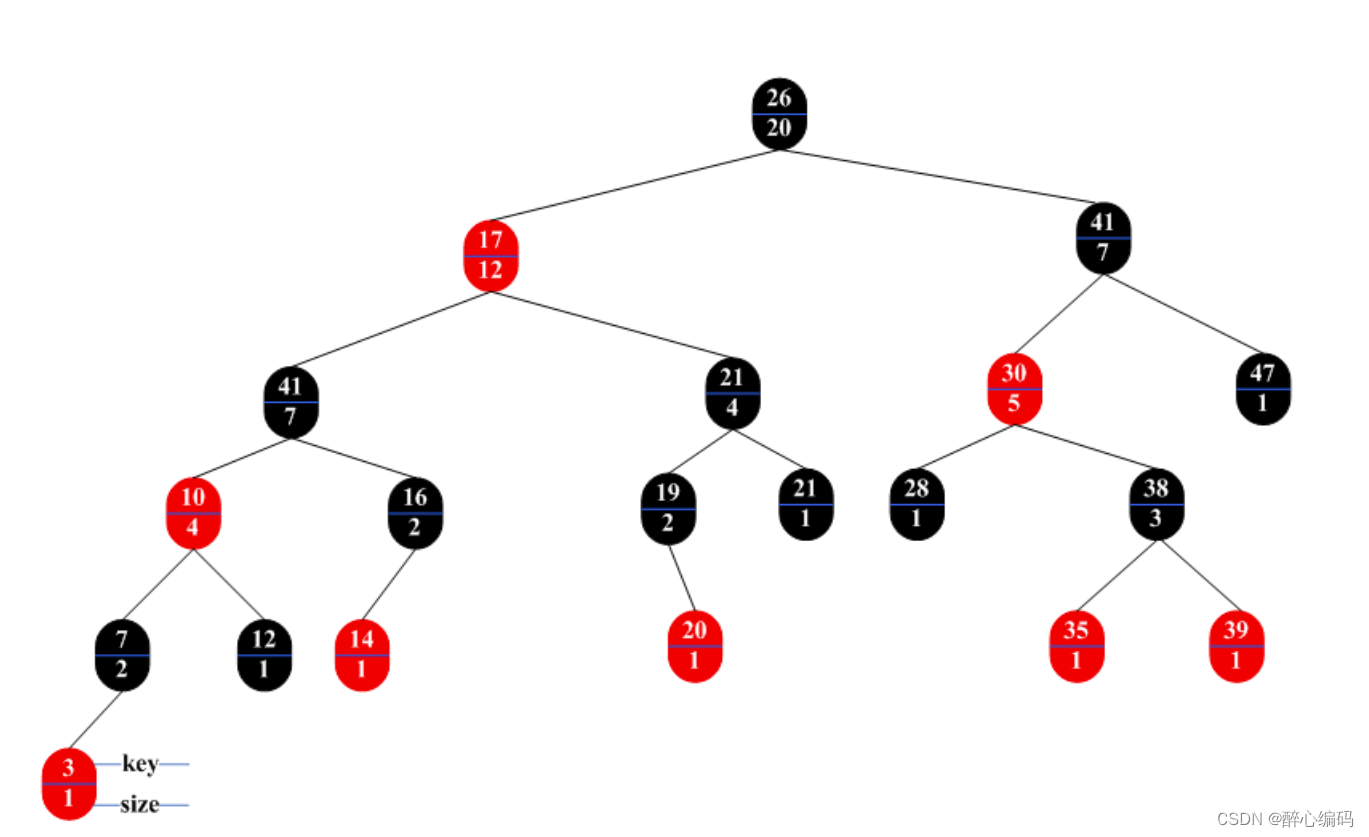
深入探索顺序统计树:实现关键字排名查询的OS-KEY-RANK递归过程
在数据结构和算法领域,顺序统计树是一种强大的工具,它允许我们在保持二叉查找树的平衡特性的同时,快速地回答关于动态集合中元素的顺序统计查询。这些查询包括确定一个给定关键字在集合中的排名,也称为秩。在本文中,我们将详细介绍一个递归过程OS-KEY-RANK(T,k),它能够在顺序统计树T中查找关键字k的秩。我们将从顺序统计树的基本概念开始,逐步深入到OS-KEY-RANK过程的设计和实现,并探讨其在实际应用中的潜在用途。
一、顺序统计树的概念
顺序统计树是一种特殊的二叉查找树,它在每个节点上存储了额外的size属性,表示以该节点为根的子树中的节点数量(包括节点本身)。这个属性使得我们能够在对数时间内回答关于集合中第k小元素的问题。顺序统计树的构建和维护需要在标准的二叉查找树操作(如插入和删除)的基础上进行额外的步骤来更新size属性。
二、秩的概念
在动态集合的上下文中,一个元素的秩是指在对该集合进行中序遍历时,该元素出现的顺序位置。例如,如果一个集合中的元素按升序排列,那么最小的元素的秩为1,第二小的元素的秩为2,依此类推。
2.1 OS-KEY-RANK过程的设计
OS-KEY-RANK过程的目标是在顺序统计树T中查找关键字k的秩。我们可以通过以下递归策略来实现这一过程:
- 如果当前节点的关键字与k相等,那么我们已经找到了目标元素,我们可以计算它的秩。
- 如果k小于当前节点的关键字,那么k可能出现在当前节点的左子树中。我们递归地在左子树中查找k的秩。
- 如果k大于当前节点的关键字,那么k可能出现在当前节点的右子树中。我们递归地在右子树中查找k的秩,并在找到k后,需要将其秩减去左子树的大小(加上当前节点本身)。
2.2 OS-KEY-RANK过程的实现
下面是OS-KEY-RANK过程的伪代码实现:
Function OS-KEY-RANK(T, k) If T is NIL Return UNDEFINED // 没有找到关键字k EndIf If k == T.key Return COUNT-RANK(T, k) ElseIf k < T.key Return OS-KEY-RANK(T.left, k) Else Return COUNT-RANK(T.left, k) + 1 + OS-KEY-RANK(T.right, k) EndIf 三、C代码示例
为了提供一个完整的C语言示例代码,我们需要定义顺序统计树的节点结构,并实现OS-KEY-RANK函数。以下是一个简化的实现,它不包括完整的红黑树特性,但提供了OS-KEY-RANK函数的核心逻辑。
首先,我们定义顺序统计树的节点结构体:
typedef struct OrderStatisticTreeNode {
int key; // 节点的关键字 int size; // 子树的大小(包括当前节点) struct OrderStatisticTreeNode *left; struct OrderStatisticTreeNode *right; struct OrderStatisticTreeNode *parent; } OrderStatisticTreeNode; 接下来,我们实现一个辅助函数,用于计算并返回给定节点的秩:
int rank(OrderStatisticTreeNode *node) {
if (node == NULL) {
return 0; } // 如果节点是叶子节点,其秩就是左子树的大小加1 if (node->left == NULL && node->right == NULL) {
return node->parent->left ? node->parent->left->size + 1 : 1; } // 如果节点有左子树,其秩是左子树的大小加上左子树中所有节点的秩 if (node->left != NULL) {
return node->left->size + 1 + rank(node->left); } // 如果节点只有右子树,其秩就是右子树的大小 return node->right->size; } 现在,我们可以实现OS-KEY-RANK函数:
OrderStatisticTreeNode* OS_KEY_RANK(OrderStatisticTreeNode* root, int k) {
OrderStatisticTreeNode *current = root; int currentRank = 1; // 用于跟踪当前节点的相对排名 while (current != NULL) {
if (k < current->key) {
// 如果k小于当前节点的关键字,我们在左子树中查找 if (current->left != NULL) {
current = current->left; } else {
// 如果没有左子树,k不在树中 return NULL; } } else if (k > current->key) {
// 如果k大于当前节点的关键字,我们在右子树中查找 if (current->right != NULL) {
current = current->right; currentRank += current->left->size + 1; // 更新排名 } else {
// 如果没有右子树,k不在树中 return NULL; } } else {
// 找到关键字k return (current->left == NULL) ? current : // 如果没有左子树,当前节点就是k current->left; // 如果有左子树,k在左子树中 } } return NULL; // 如果循环结束,表示k不在树中 } 最后,我们提供一个简单的主函数,用于测试OS-KEY-RANK函数:
int main() {
// 这里应该包含顺序统计树的构建和初始化代码 // ... // 假设我们有一个顺序统计树的根节点 OrderStatisticTreeNode* T_root = createOrderStatisticTree(); // 需要实现这个函数 // 假设我们要找到关键字为k的元素的秩 int k = 10; OrderStatisticTreeNode* foundNode = OS_KEY_RANK(T_root, k); if (foundNode != NULL) {
printf("The rank of key %d is %d\n", k, rank(foundNode)); } else {
printf("Key %d not found in the tree.\n", k); } return 0; } 请注意,上述代码是一个简化的示例,它没有包括完整的顺序统计树实现,也没有处理红黑树插入和删除操作中的自平衡逻辑。在实际应用中,你需要一个完整的顺序统计树实现,包括节点的插入、删除和size属性的更新等操作。此外,上述代码也没有进行错误检查,例如检查输入的关键字是否有效。在生产代码中,这些检查是必要的。
在这个伪代码中,COUNT-RANK是一个辅助函数,它计算关键字k在子树中的排名。为了简化描述,我们假设COUNT-RANK函数已经实现,并且在给定的子树中查找k的排名。
四、递归过程的详细分析
递归过程OS-KEY-RANK的核心在于它能够沿着二叉查找树的路径快速定位关键字k所在的区域,并计算出k的秩。在递归下降过程中,我们不断地将问题规模缩小,直到找到包含k的子树。一旦发现了k,我们就可以通过计算左子树中的节点数量来确定k的秩。
五、OS-KEY-RANK的实际应用
OS-KEY-RANK过程在许多实际应用中都非常有用。例如,在数据库系统中,我们可能需要快速确定一个给定值在排序后的数据集中的位置。在统计分析中,我们可能需要找到某个数值在整个数据集中的百分位数。在机器学习算法中,OS-KEY-RANK可以帮助我们快速找到排序后的数据集中的特定元素,这对于构建高效的排序算法和索引结构至关重要。
六、结论
在本文中,我们详细介绍了顺序统计树的概念,并展示了如何设计和实现一个递归过程OS-KEY-RANK,它能够在顺序统计树中查找给定关键字的秩。通过这个过程,我们可以在对数时间内回答关于动态集合中元素的顺序统计查询。OS-KEY-RANK过程的设计和实现展示了递归技术在解决复杂数据结构问题中的优雅和效率,同时也体现了顺序统计树在处理排序和排名问题时的强大能力。随着数据规模的不断增长,顺序统计树和相关算法将在未来的计算机科学和软件工程领域扮演越来越重要的角色。
今天的文章
顺序数据的统计方法_输入一组数据,并从小到大排序分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/81327.html