梯度下降算法可以求解什么值_梯度grad计算公式「建议收藏」

如对博文有任何疑问，请留言。

一、方向导数

方向导数：类比于函数的偏导数是函数沿坐标轴方向的变化率，方向导数是函数沿某一方向的变化率。

定理：如果函数 $f(x,y)$ 在点 $P_0(x_0,y_0)$ 可微分，那么函数在该点沿任一方向 $l$ 的方向导数存在，且有
$${\frac{\partial f}{\partial l}|}_{(x_0,y_0)}=f_x(x_0,y_0)\cos \alpha +f_y(x_0,y_0)\cos \beta \text{\hspace{1em}(1)}$$
其中 $\cos \rho$ 和 $\cos \beta$ 是方向 $l$ 的方向余弦。

二、梯度

梯度：梯度是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（梯度的方向）变化最快，变化率最大（为梯度的模）。

另一种理解：在微积分里，对多元函数的参数求偏导，把求得的各个参数的偏导以向量的形式写出来，就是梯度。

定义：设二元函数 $z=f(x,y)$ 在平面区域D上具有一阶连续偏导数，则对与于每一个点 P(x,y) 都可定出一个向量 $\left\{\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right\}=f_x(x,y)\vec{i}+f_y(x,y)\vec{j}$ ，该函数就称为函数 $z=f(x,y)$ 在点 P(x,y) 的梯度，记作 $gradf(x,y)$ 或 $\nabla f(x,y)$ ，既有：
$$gradf(x,y)=\nabla f(x,y)=\left\{\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right\}=f_x(x,y)\vec{i}+f_y(x,y)\vec{j}\text{\hspace{1em}(2)}$$

注意，梯度是在多元函数中的，如果要拓展到一元函数，则要这样理解：它是一个标量，并且在某点的梯度等于这一点的导数。

三、梯度下降算法数学推导

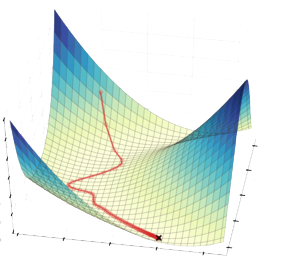
梯度下降算法针对的是最小优化问题(即求最小值问题)，目的是使目标函数沿最快路径下降到最小值。

通俗的解释，是模拟下山，每次沿着当前位置最陡峭最易下山的方向前进一小步，然后继续沿下一个位置最陡方向前进一小步。这样一步一步走下去，一直走到觉得我们已经到了山脚。

虽然这样很好理解，但这只是给不懂梯度下降算法的小白讲的形象比喻，最终要落实到算法上代码上，具体的过程是怎么样的呢？还得靠数学推导。

算法作用于损失函数(也称目标函数、代价函数、误差函数)，是为了找到使损失函数取最小值的权重($w$)和偏置($b$)。

设损失函数为 $l(x,w,b,y)$ ，要寻找最优的 $w$ 和 $b$ ，为便于计算，抽象出函数描述 $f(w,b)$ ，这里 $f=l$ ，只是描述形式不同。同时设 $\theta =(w,b{)}^T$ ，$T$ 为转置符号，此时 $\theta$ 是一个二维列向量。

则损失函数为 $f(\theta )$，将其进行一阶泰勒展开，得：
$$f(\theta )\approx f({\theta }_0)+(\theta -{\theta }_0)\cdot \nabla f({\theta }_0)\text{\hspace{1em}(3)}$$

为什么要一阶泰勒展开呢，因为这样可以“以直代曲”，数学术语叫“局部线性近似”，就是在很小的区间内，直线与曲线近似重合，对曲线不易做的计算，可以对直线计算作为代替。

$\theta -{\theta }_0$ 就是这个很小的区间，可以表示为 $\Delta \theta$ ，但它仍然是一个矢量，将其分解为模和单位向量的形式，即长度和方向的形式：
$$\Delta \theta =\theta -{\theta }_0=\rho \vec{v}\text{\hspace{1em}(4)}$$
这里的 $\rho$ 就是前面下山比喻中每次走的一小步的距离(步长)，$\vec{v}$ 就是走的方向，这里注意$\rho$ 是距离(长度)，所以 $\rho$ > 0。

则损失函数 $f(\theta )$ 的一阶泰勒展开式可描述为：
$$f(\theta )\approx f({\theta }_0)+\rho \vec{v}\cdot \nabla f({\theta }_0)\text{\hspace{1em}(5)}$$

其中 $f({\theta }_0)$ 是现在的损失函数的值，$f(\theta )$ 是即将要更新的损失函数的值，前面说过我们的目的是为了找到使损失函数取最小值的权重($w$)和偏置($b$)，所以我们每次更新要保证 $f(\theta )<f({\theta }_0)$ ，即：
$$f(\theta )-f({\theta }_0)\approx \rho \vec{v}\cdot \nabla f({\theta }_0)<0\text{\hspace{1em}(6)}$$
又因为 $\rho$ > 0，所以有：
$$\vec{v}\cdot \nabla f({\theta }_0)<0\text{\hspace{1em}(7)}$$
这里注意，$\vec{v}$ 是一个向量，$\nabla f({\theta }_0)$ 是函数 $f(w,b)$ 在点 $(w_0,b_0)$ 处的梯度，它也是一个向量。要两个向量的乘积小于0，则需要他们的夹角大于90°。再次想到我们的目的，使目标函数沿 最快 路径下降到最小值，既然要最快，$f(\theta )$ 与 $f({\theta }_0)$ 的距离（即 $|f(\theta )-f({\theta }_0)|$）就要越大越好，根据公式 $f(\theta )-f({\theta }_0)\approx \rho \vec{v}\cdot \nabla f({\theta }_0)<0$ ，就是结果越小越好（因为结果是负值）。再回到 $\vec{v}$ 和 $\nabla f({\theta }_0)$ 两个向量的乘积上，就是他们的夹角为180°时，$\vec{v}\cdot \nabla f({\theta }_0)$ 的结果最小（这里也是为什么要沿着梯度反方向更新自变量的原因），此时结果为：
$$\vec{v}\cdot \nabla f({\theta }_0)=-||\vec{v}||\cdot ||\nabla f({\theta }_0)||=-||\nabla f({\theta }_0)||\text{\hspace{1em}(8)}$$
由于 $\vec{v}$ 是单位向量，则 $\vec{v}$ 描述为：
$$\vec{v}=-\frac{\nabla f({\theta }_0)}{||\nabla f({\theta }_0)||}\text{\hspace{1em}(9)}$$
带入 $\theta -{\theta }_0=\rho \vec{v}$ 得：
$$\theta ={\theta }_0-\rho \frac{\nabla f({\theta }_0)}{||\nabla f({\theta }_0)||}\text{\hspace{1em}(10)}$$
因为 $\rho$ 和 $\frac{1}{||\nabla f({\theta }_0)||}$ 都是标量，所以可以设 $\alpha =\frac{\rho }{||\nabla f({\theta }_0)||}$ ，则上式（梯度下降算法中 $\theta$ 的更新表达式）可描述为：
$$\theta ={\theta }_0-\alpha \nabla f({\theta }_0)={\theta }_0-\alpha \frac{\partial }{\partial {\theta }_0}f(\theta )\text{\hspace{1em}(11)}$$
这里的 $\alpha$ 就是我们常说的学习速率。

另外，这个公式还有一种比较专业的描述方法：
$$\theta \leftarrow {\theta }_0-\alpha \frac{\partial }{\partial {\theta }_0}f(\theta )\text{\hspace{1em}(12)}$$
这个公式就是最终往代码里写的形式，只不过要结合你的 $f$ (损失函数)的具体形式进一步计算偏导，再落实到代码。

实际使用该算法时，有时将公式写成分量的形式，即将 $\theta =(w,b{)}^T，{\theta }_0=(w_0,b_0{)}^T$ 代入上式得：
$$(w,b{)}^T=(w_0,b_0{)}^T-\alpha {\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right)}^T\text{\hspace{1em}(13)}$$
即：
$$\begin{array}{r}w=w_0-\alpha \frac{\partial f}{\partial w_0}\\ b=b_0-\alpha \frac{\partial f}{\partial b_0}\end{array}\text{\hspace{1em}(14)}$$

它们的意思是一样的，只是表示方法不同。但分量形式不常用，多用向量形式。

以上是梯度下降算法自变量更新的数学推导，那么什么时候停止更新呢，你肯定会说当然是找到使损失函数取最小值的权重($w$)和偏置($b$)时，没错这也是我们前面算法目的中的描述。但是怎样知道找到了损失函数的最小值呢，实际应用中不会真的一直迭代到损失函数的最小值，而是在精度和训练时间都可接受的范围内，尽可能的接近最小值，在资源消耗和精度要求间权衡。具体结束条件通常为：

1. $||\nabla f({\theta }_0)||$ 的值足够小。（也可以说是损失函数不再明显的减小，但同时也要兼顾损失函数的值，否则就要检查初始参数和训练数据等），实际编程时，考虑到程序性能，不一定以直接判断损失函数的值为依据，也可以间接判断(比如误差值)。
2. 迭代次数达到预定值。

这里讲的是梯度下降算法的核心思想，最后实际应用还要落实到具体算法，梯度下降算法家族包括批量梯度下降法（Batch Gradient Descent，BGD，也叫最速梯度下降法）、随机梯度下降法（Stochastic Gradient Descent，SGD）、小批量梯度下降法（Mini-Batch Gradient Descent，MBGD）三种。它们的算法原理相同，只是在输入数据时采取不同的策略。

四、批量梯度下降法代码实现

4.1 选择损失函数与模型

损失函数选择均方差损失函数(MSE)，其表达式为：
$$L(\theta ;x,y)=\frac{1}{M}\sum _{i=1}^M(\hat{y}(x_i,\theta )-y_i{)}^2\text{\hspace{1em}(15)}$$
其中：

$\hat{y}$ — — 预测函数，

$x,y$ — — 分别是训练数据的输入值与标签值，

$\theta$ — — 是 $w$ 和 $b$ 组成的向量，

$M$ — — 是训练数据个数 。

预测模型(函数)选择线性回归模型，表达式为：
$$\hat{y}(x,\theta )=\sum _{j=0}^n{\theta }_j{x}_j\text{\hspace{1em}(16)}$$
其中：

$x$ — — 是预测输入数据点，

$\theta$ — — 是学习得到的权重($w$)和偏置(b)。

$n$ — — 是输入数据的维数。

4.2 从公式到代码

首先确定目的，是为了找到使损失函数取最小值的权重($w$)和偏置($b$)。我们找到了吗？我们找到了。他们的计算式就是公式 $(12)$ ，所以我们的代码核心部分就是实现公式 $(12)$ ，对于这个公式，重要的部分是 $\frac{\partial }{\partial {\theta }_0}f(\theta )$，损失函数对 $\theta$ 的偏导数，我们的损失函数已由公式 $(15)$ 给出，即 $f(\theta )=L(\theta ;x,y)$，公式 $(15)$ 对 $\theta$ 求偏导得：
$$\begin{array}{rl}\frac{\partial }{\partial {\theta }_0}f(\theta )& =\frac{\partial }{\partial {\theta }_0}(\hat{y}(x,{\theta }_0)-y{)}^2\\ & =2\cdot (\hat{y}(x,{\theta }_0)-y)\cdot \frac{\partial }{\partial {\theta }_0}(\hat{y}(x,{\theta }_0)-y)\\ & =2\cdot (\hat{y}(x,{\theta }_0)-y)\cdot \frac{\partial }{\partial {\theta }_0}\left(\sum _{j=0}^n{\theta }_j{x}_j-y\right)\\ & =2\cdot (\hat{y}(x,{\theta }_0)-y)\cdot x\end{array}\text{\hspace{1em}(17)}$$

将公式 $(17)$ 代入公式 $(12)$ 得：
$$\theta \leftarrow {\theta }_0-\alpha \cdot 2\cdot (\hat{y}(x,{\theta }_0)-y)\cdot x\text{\hspace{1em}(18)}$$
其中 $\hat{y}$ 是预测函数，${\theta }_0$ 代表当前值，$\theta$ 是下一次的更新值，$x,y$ 是训练数据的输入值与标签值，$\alpha$ 是学习率，由于 $2$ 是常数，$\alpha$ 是标量，可以将 $2$ 并入 $\alpha$ ，则实际上的 $\alpha$ 为 $\frac{2\rho }{||\nabla f({\theta }_0)||}$ ，可见学习率可以表达梯度下降迭代步长的变化，实际应用中常常人为赋值或使用特定策略赋值，而不是使用原公式。

至此，公式 $(18)$ 可描述为：
$$\theta \leftarrow {\theta }_0-\alpha \cdot (\hat{y}(x,{\theta }_0)-y)\cdot x\text{\hspace{1em}(19)}$$
这是最后写入程序的公式。

为了编程方便，将公式分解，令：

$$hypothesis=\hat{y}(x,{\theta }_0)\text{\hspace{1em}(20)}$$

$$error=\hat{y}(x,{\theta }_0)-y=hypothesis-y\text{\hspace{1em}(21)}$$

$$gradient=(\hat{y}(x,{\theta }_0)-y)\cdot x=(error\cdot x)/m\text{\hspace{1em}(22)}$$

$$\theta ={\theta }_0-\alpha \cdot gradient\text{\hspace{1em}(23)}$$

关于 gradient 的计算，这里说明一下，梯度下降算法家族的三个算法的不同之处就在这里。

批量梯度下降法(BGD)：每次迭代计算梯度，使用整个数据集($m=M$)，也就是每次计算 gradient 都用上所有数据点，然后求均值。

随机梯度下降法(SGD)：每次迭代计算梯度，从整个数据集中随机选取一个数据点($m=1$)。

小批量梯度下降法(MBGD)：每次迭代计算梯度，从整个数据集中选取一个小批量数据($1<m<M$)。

以下根据公式 $(20)、(21)、(22)、(23)$ 编写代码，实现批量梯度下降法：

def batchGradientDescent(x, y, theta, alpha, m, maxInteration):
    '''批梯度下降算法简单实现 x: 输入 y: 输出 theta: w 和 b 组成的向量 alpha: 学习率 m: 批数据数量 maxInteration：最大迭代次数 '''
    x_train = x.transpose() # 转置
    for i in range(0, maxInteration):
        # 预测值
        hypothesis = np.dot(x, theta)
        # 预测误差
        error = hypothesis - y
        # 下降梯度
        gradient = np.dot(x_train, error) / m
        # 更新theta
        theta = theta - alpha * gradient
    return theta

同理，随机梯度下降代码为：

def stochasticGradientDescent(x, y, theta, alpha, maxInteration):
    '''批梯度下降算法简单实现 x: 输入 y: 输出 theta: w 和 b 组成的向量 alpha: 学习率 m: 批数据数量 maxInteration：最大迭代次数 '''
    data = []
    for i in range(4):
        data.append(i)
    for i in range(0, maxInteration):
        hypothesis = np.dot(x, theta)
        # 预测误差
        error = hypothesis - y
        # 选取一个随机数
        index = random.sample(data, 1)  # 从列表data中随机选取一个数据
        index1 = index[0]
        # 下降梯度
        gradient = error[index1] * x[index1]
        # 求导之后得到theta
        theta = theta - alpha * gradient
    return theta

小批量梯度下降：

def miniBatchGradientDescent(x, y, theta, alpha, m, batch_size, epochs):
    ''' x: 输入 y: 输出 theta: w 和 b 组成的向量 alpha: 学习率 m: 数据集的数据量 batch_size：一个批次的数据量 epochs：数据集最大迭代次数 '''
    for epoch in range(epochs):
        # 生成索引列表
        indexs_list = np.arange(m)
        # 按批次迭代
        for batch in range(m // batch_size):
            # 生成批次数据索引
            index_list = indexs_list[batch*batch_size : batch*batch_size+batch_size]
            # 获取批次数据
            x_batch = x[index_list]
            y_batch = y[index_list]
            # 预测值
            hypothesis = np.dot(x_batch, theta)
            # 预测误差
            error = hypothesis - y_batch
            # 下降梯度
            gradient = np.dot(x_batch.T, error) / m
            # 更新theta
            theta = theta - alpha * gradient
    return theta

五、总结及其他的一些说明

梯度下降运行步骤：

1. 用随机值初始化权重和偏差

2. 把输入传入网络，得到输出值(预测值)

3. 计算预测值和真实值(标签值)之间的误差

4. 对每一个产生误差的神经元，调整相应的（权重和偏差）值以减小误差

5. 重复迭代，直至得到网络权重和偏差的最佳值

批量梯度下降法(BGD)：每次迭代计算梯度，使用整个数据集。每次更新都会朝着正确的方向进行，最后能够保证收敛于极值点，凸函数收敛于全局极值点，非凸函数可能会收敛于局部极值点，缺陷就是学习时间太长，消耗大量内存。

随机梯度下降法(SGD)：每次迭代计算梯度，从整个数据集中随机选取一个数据，所以每次迭代的时间非常快。但收敛时震荡，不稳定，在最优解附近波动，难以判断是否已经收敛。

小批量梯度下降法(MBGD)：这个是 BGD 和 SGD 的折中方法， BGD 每次使用整体数据，收敛太慢， SGD 每次只使用一条数据，虽然收敛快但震荡厉害，所以出现了折中的 MBGD，每次使用 n 条数据，如果 n(batch size) 选择的合适，不仅收敛速度比SGD更快、更稳定，而且在最优解附近的震荡也不会很大，甚至得到比 BGD 更好的解。

batch size 的选择，一般取2的幂次时能充分利用矩阵运算操作，因此可以在2的幂次中挑选最优取值。例如16、32、64、128、256等等。

另外，还有一种小批量随机梯度下降法，即在小批量梯度下降法中，获取批次数据时，不是按原有输入顺序选取数据，而是先把原有输入数据打乱，再选取批次数据，代码如下：

def mini_batch_stochastic_gradient_descent(x, y, theta, alpha, m, batch_size, epochs):
    ''' x: 输入 y: 输出 theta: w 和 b 组成的向量 alpha: 学习率 m: 数据集的数据量 batch_size：一个批次的数据量 epochs：数据集最大迭代次数 '''
    for epoch in range(epochs):
        # 生成索引列表
        data_index = np.arange(m)
        # 打乱样本顺序
        np.random.shuffle(data_index)
        # 按批次迭代
        for batch in range(m // batch_size):
            # 生成批次数据索引
            batch_index = data_index[batch*batch_size : batch*batch_size+batch_size]
            # 获取批次数据
            x_batch = x[batch_index]
            y_batch = y[batch_index]
            # 预测值
            hypothesis = np.dot(x_batch, theta)
            # 预测误差
            error = hypothesis - y_batch
            # 下降梯度
            gradient = np.dot(x_batch.T, error) / m
            # 更新theta
            theta = theta - alpha * gradient
    return theta

参考：
梯度（数学名词）_百度百科

简单的梯度下降算法，你真的懂了吗？

解梯度下降法的三种形式BGD、SGD以及MBGD

今天的文章梯度下降算法可以求解什么值_梯度grad计算公式「建议收藏」分享到此就结束了，感谢您的阅读。