哈夫曼树 数据结构_哈夫曼树只有度为0和度为2

1、基本概念

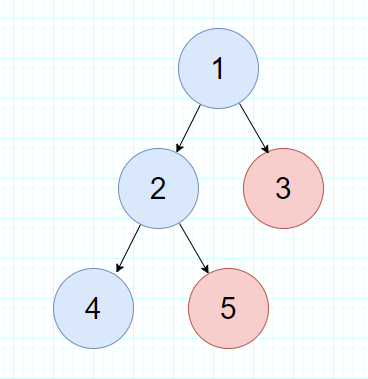
• 路径：一棵树中，从一个结点到另一个结点所经过的所有结点，被我们称为两个结点之间的路径，如图：
  
  从根节点1到叶子节点4的路径:1,2,4

• 路径长度：在一棵树中，从一个结点到另一个结点所经过的“边”的数量，被我们称为两个结点之间的路径长度，还是上图，根节点1到叶子结点4的路径经过了2个边，也就是说，若规定根节点的层数为1，则从根节点到N层的结点的的路径长度为：N-1

• 结点的带权路径长度：树的每一个结点，都可以拥有自己的“权重”（Weight），权重在不同的算法当中可以起到不同的作用。结点的带权路径长度，是指树的根结点到该结点的路径长度，和该结点权重的乘积,还是上图，如结点4的权重是10，那结点4的带权路径长度就是10*2 = 20。

• 树的带权路径长度：在一棵树中，所有叶子结点的带权路径长度之和，被称为树的带权路径长度，也被简称为WPL。

2、什么是哈夫曼树？

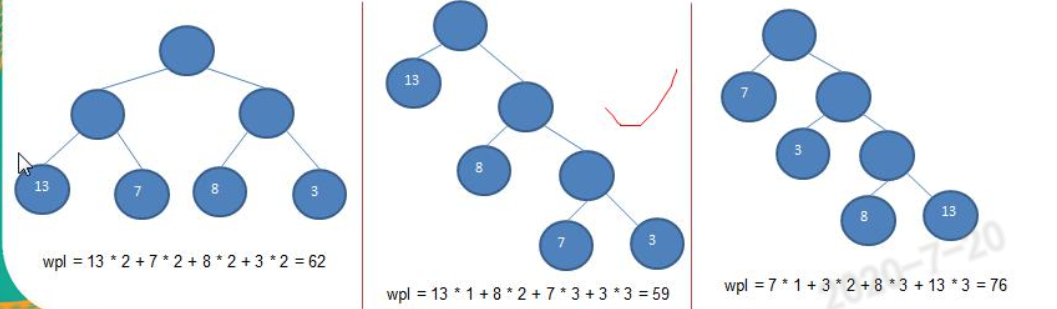
• 给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。
• 哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

• WPL最小的就是哈夫曼树

3、哈夫曼树构建图解

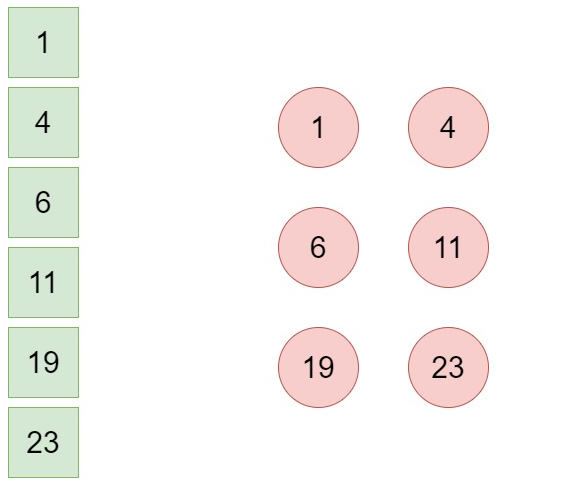
• 给定一个数列：

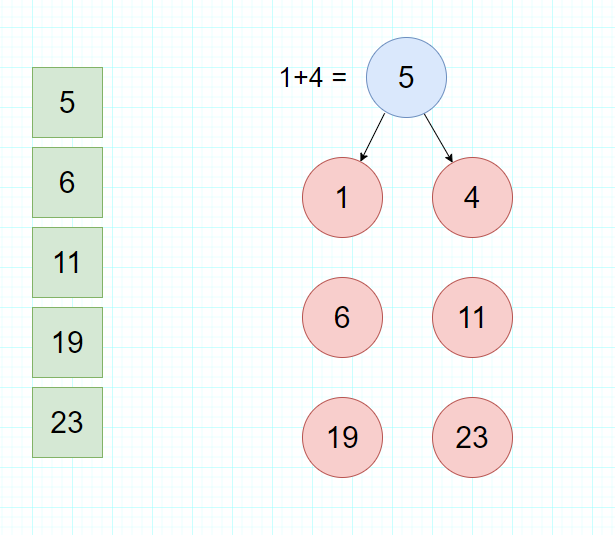
• 第一步：把每一个叶子结点，都当做树一颗独立的树（只有根结点的树），同时建个辅助队列，按照权值从小到大存储了所有叶子结点，用于后续哈夫曼树的构建辅助。

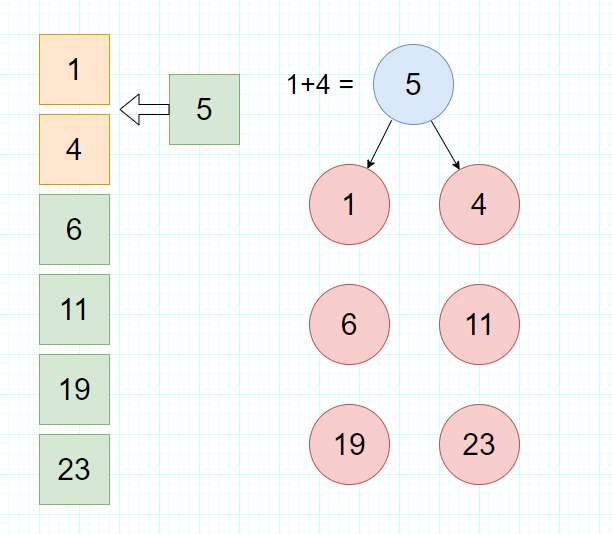
• 第二步：选择当前权值最小的两个结点，生成新的父结点，借助辅助队列，我们可以找到权值最小的结点1和4，并根据这两个结点生成一个新的父结点，父节点的权值是这两个结点权值之和。

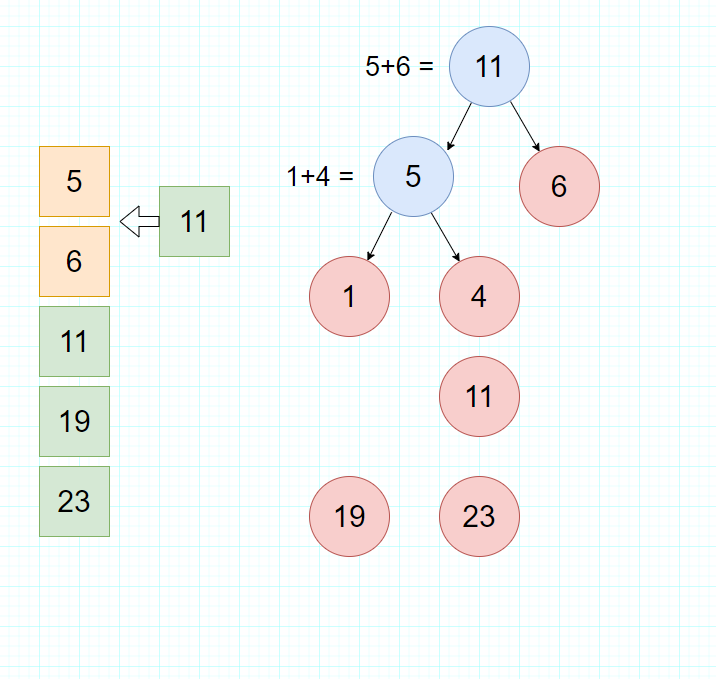
• 第三步：从队列中移除上一步选择的两个最小结点，把新的父节点加入队列

也就是从队列中删除1和4，插入5，并且仍然保持队列的升序。

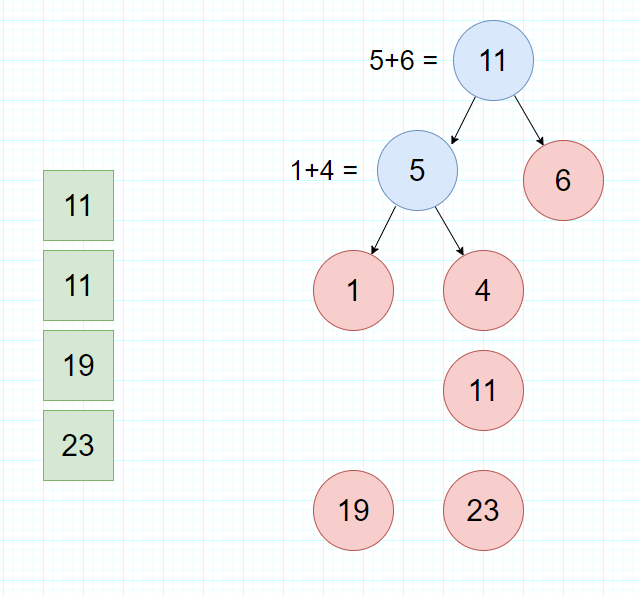
• 第四步：继续选择当前权值最小的两个结点，生成新的父结点。

• 第五步：继续移除上一步选择的两个最小结点，把新的父节点加入队列。

• 第六步：继续选择当前权值最小的两个结点，生成新的父结点。

今天的文章哈夫曼树 数据结构_哈夫曼树只有度为0和度为2分享到此就结束了，感谢您的阅读。