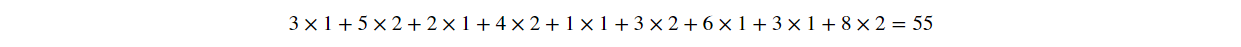反卷积的作用_用matlab两个序列卷积

什么是卷积

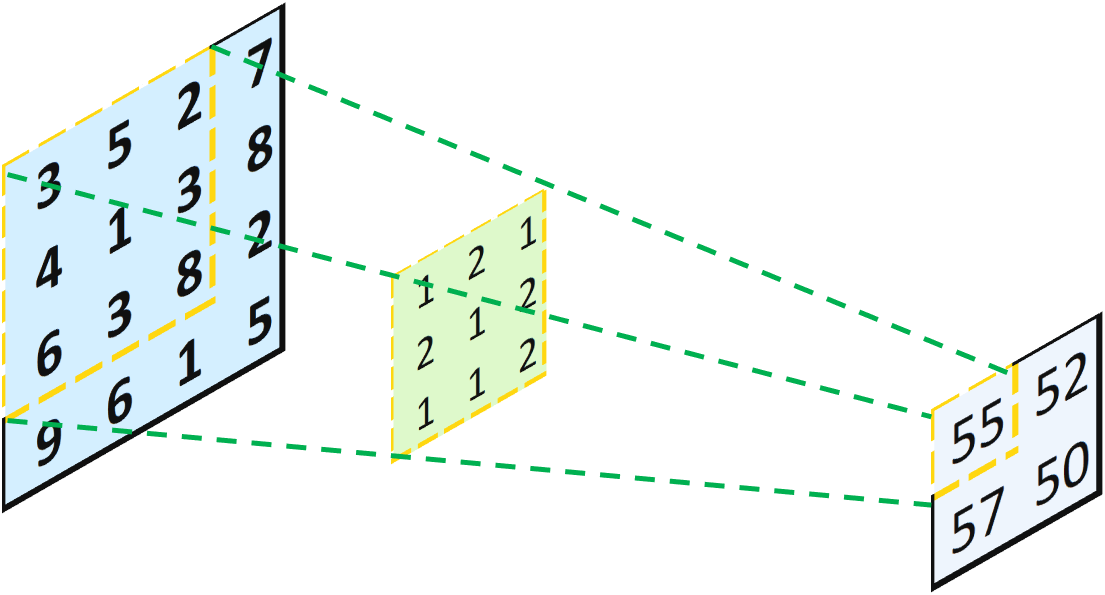
卷积就是把卷积核放在输入上进行滑窗，将当前卷积核覆盖范围内的输入与卷积核相乘，值进行累加，得到当前位置的输出，其本质在于融合多个像素值的信息输出一个像素值，本质上是下采样的，所以输出的大小必然小于输入的大小，如下图所示：

什么是反卷积

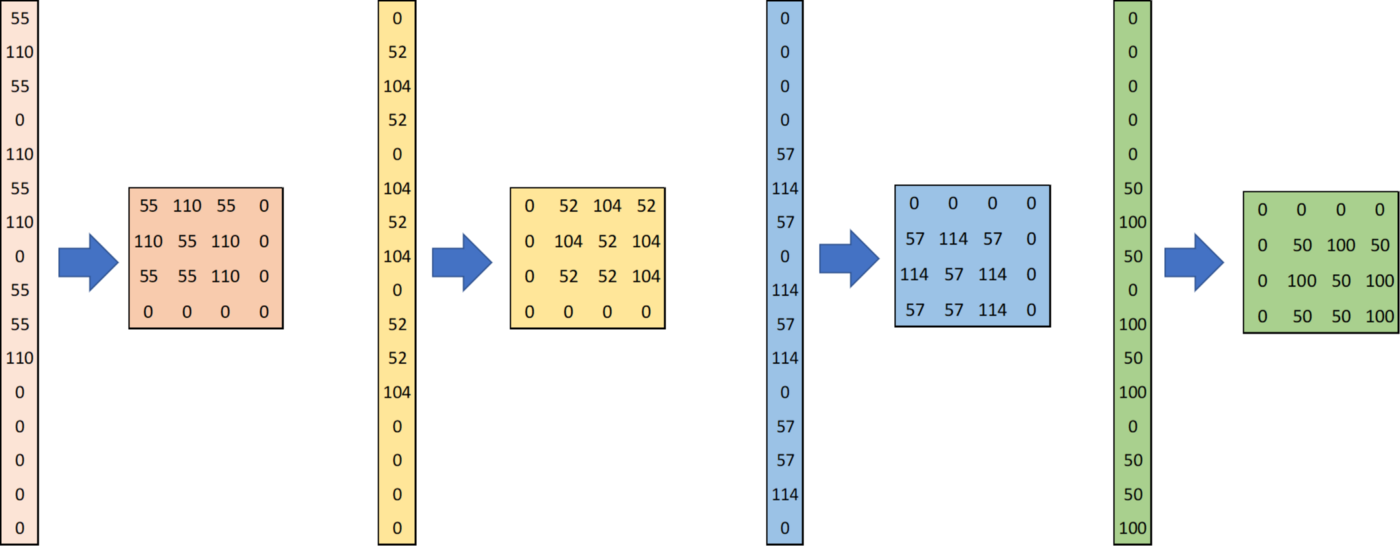
反卷积和转置卷积都是一个意思，所谓的反卷积，就是卷积的逆操作，我们将上图的卷积看成是输入通过卷积核的透视，那么反卷积就可以看成输出通过卷积核的透视，具体如下图所示：

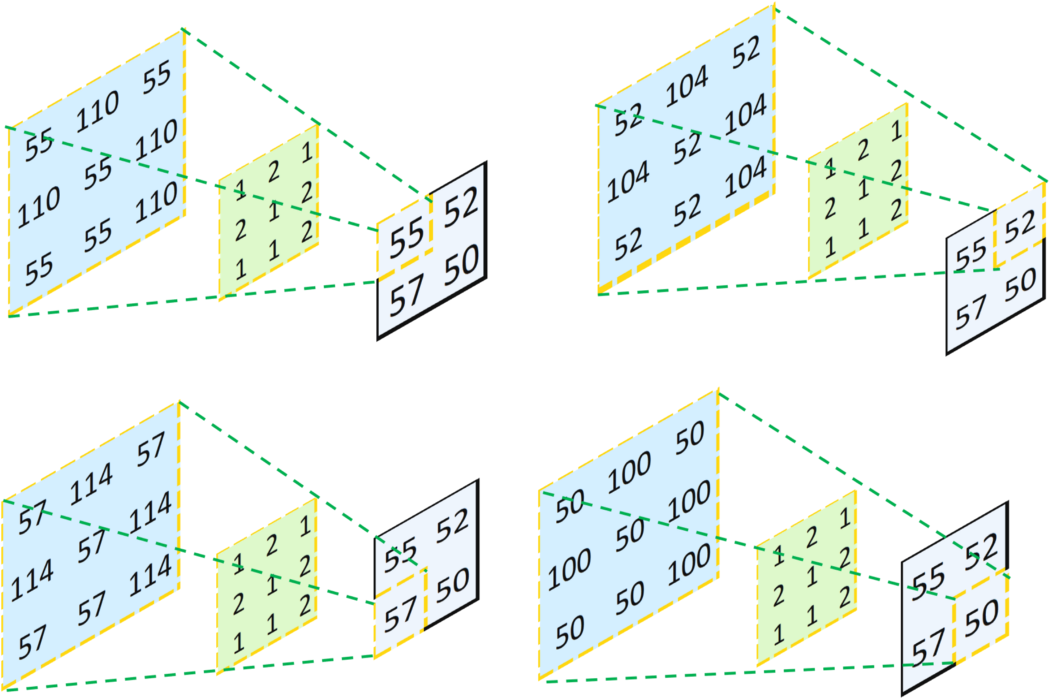
比如左上角的图，将输出的55按照绿色的线的逆方向投影回去，可以得到[[55,110,55],[110,55,110],[55,55,110]]的结果；
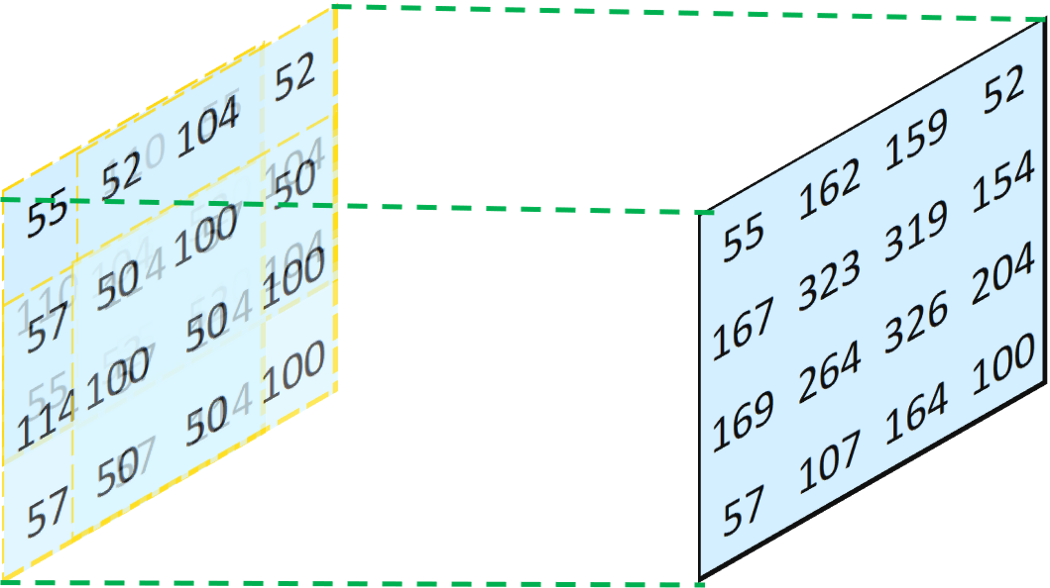
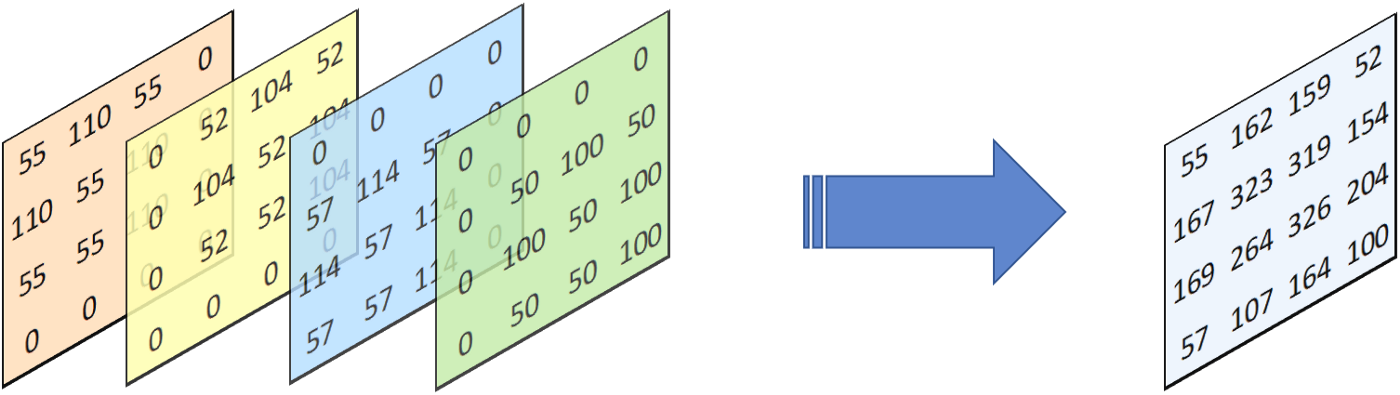
我们将得到的四张特征图进行叠加（重合的地方其值相加），可以得到下图：

最终我们得到的特征图与卷积输入的特征图值的大小并不相同，说明卷积和反卷积并不是完全对等的可逆操作（因为采用相同的卷积核，卷积和反卷积得到的输入输出不同），也就是反卷积只能恢复尺寸，不能恢复数值

反卷积(deconv)为何能被称作转置卷积(Transposed conv)

因为反卷积就是将卷积操作中的卷积核矩阵进行了转置！！！！
下面详细来说：
我们知道，卷积在框架中的底层实现是通过矩阵相乘的方式，仍然以第一个卷积的例子来说：
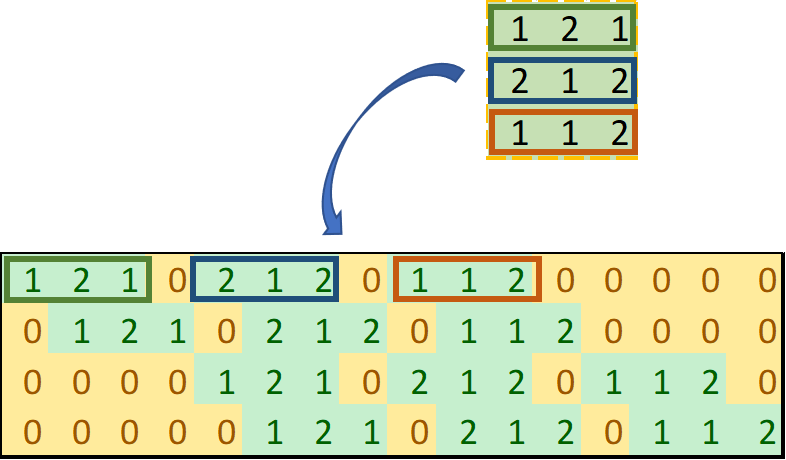
我们将3X3的卷积核变换成4X16的矩阵，如下图所示：

为什么要将3X3的卷积核变换成4X16的矩阵呢？
原因：
1.在我们最开始讲到的卷积的例子当中，对于4X4的输入而言，卷积核一共要放置4次（移动四次），一次在原位置，一次横向移动一下，再纵向移动一下，再横向移动一下，把输入看成一维的向量的话，就有了以上的卷积核矩阵；
2.为什么要补0变成16维呢？因为是为了矩阵相乘，我们的输入是4X4，打成一维的就是1X16，当单个卷积核卷积的时候，另外7个值是没有参与计算的，所以要补7个0；
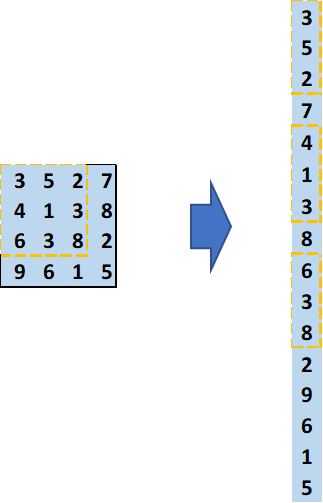
接下来，我们将4X4的输入变成16X1的矩阵，如下图所示：

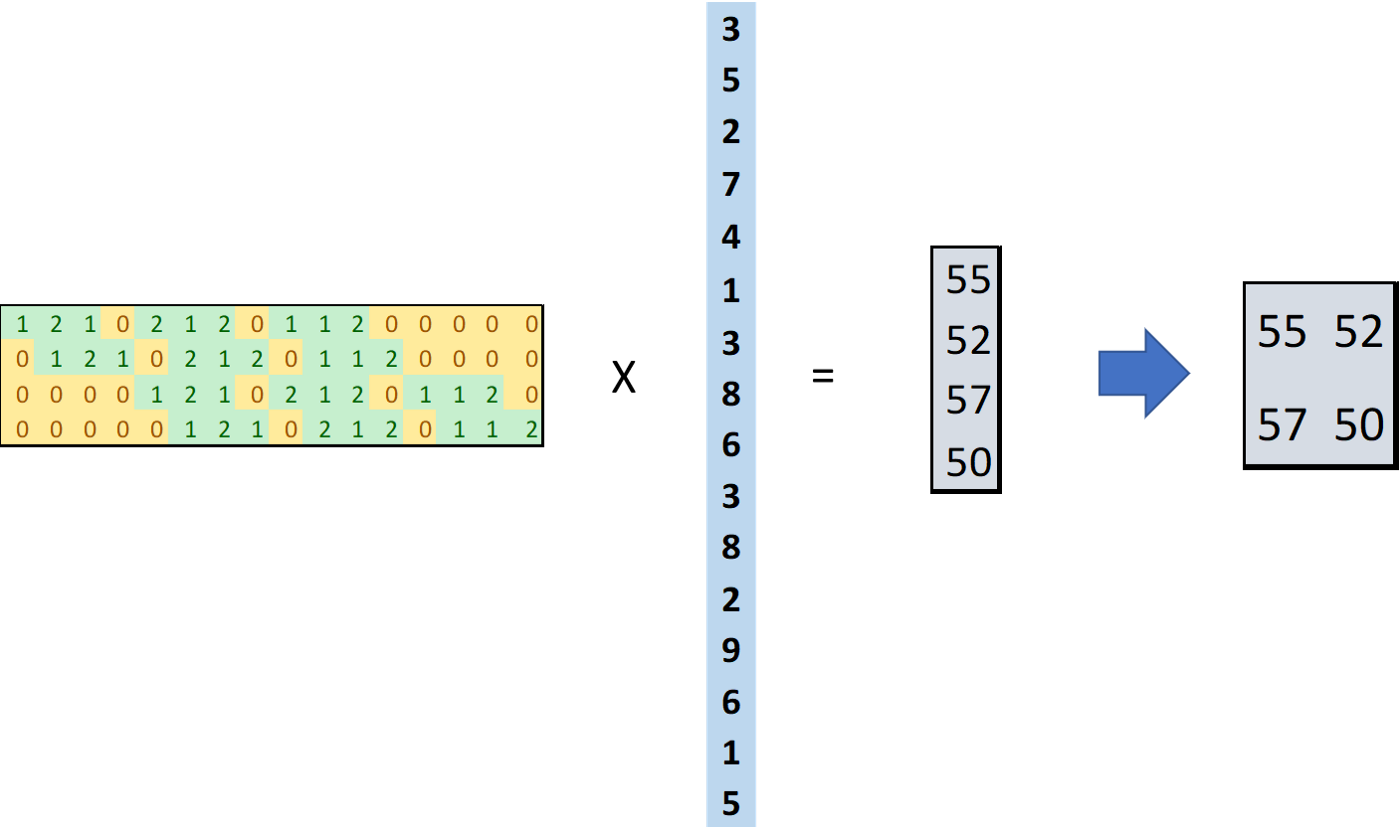
然后矩阵相乘再进行reshape即可得到卷积的结果：

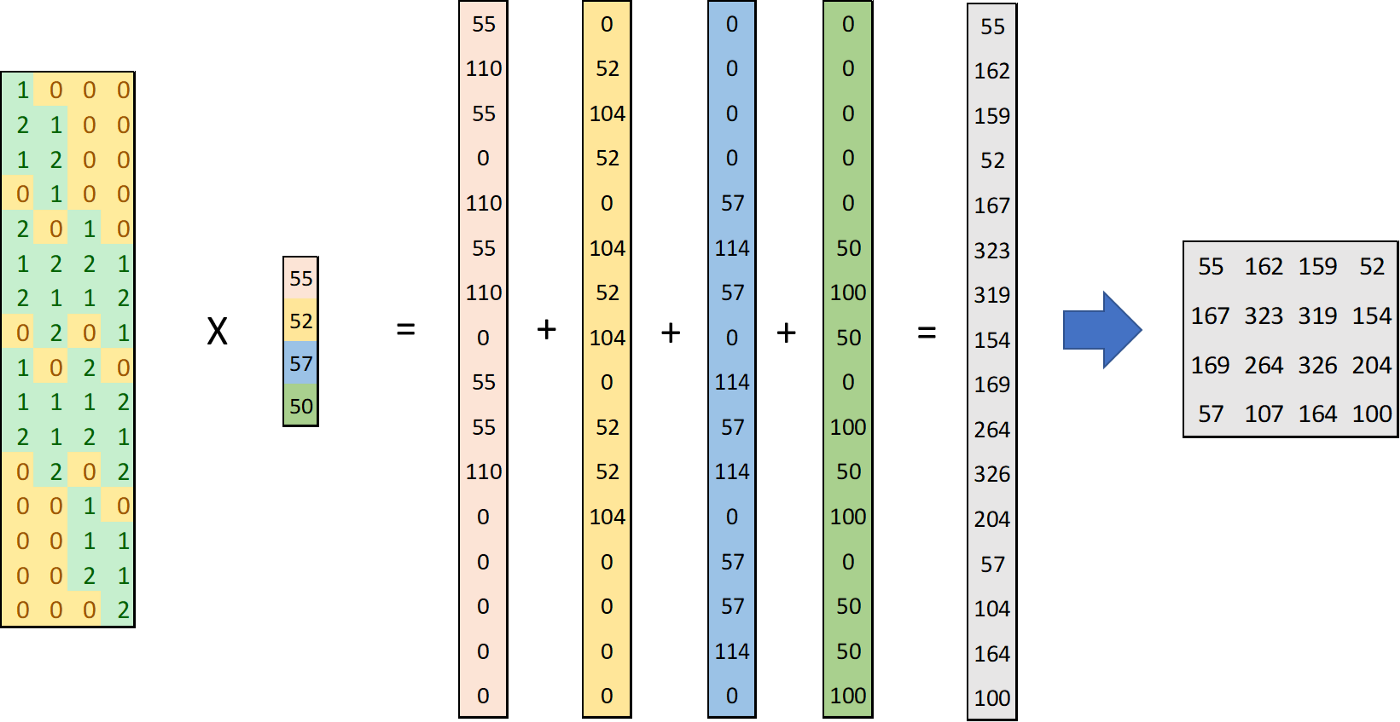
然后我们反卷积是如何实现的，如下图所示：

在反卷积中，将4X16的卷积核进行了转置，与1X4的输入相乘，四个中间过程可以代表矩阵相乘过程中的中间结果；
将中间结果reshape成4X4,再相加，可以得到与我们之前介绍反卷积推导相同的中间流程；

今天的文章反卷积的作用_用matlab两个序列卷积分享到此就结束了，感谢您的阅读。