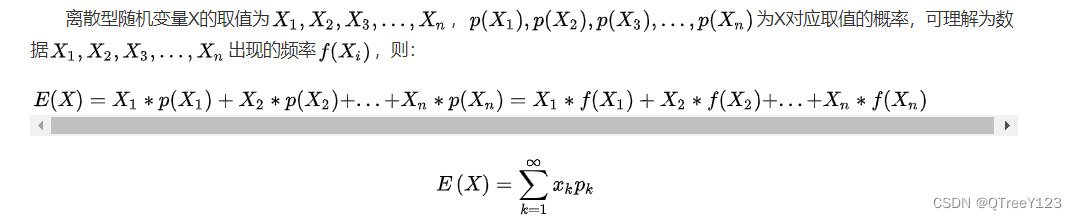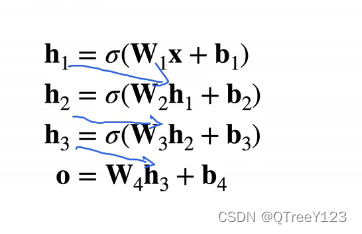前向传播和反向传播的区别_神经网络dropout的概念

目录

一：回顾

二：暂退法（dropout）

 三：实践中的暂退法

 四：从零开始实现

定义模型参数定义模型

训练和测试

五：前向传播和后向传播

正向传播： 

正向传播完成：

 反向传播

 继续反向传播w1

 更新w1的值

把所有的w都更新一遍，反向传播的一轮就结束了

六：总结：

所有项目代码+UI界面

一：回顾

        上次提到了L1L2正则化能缓解过拟合的现象，L1正则化体现了稀疏性（即在某些项有值，而其他项为0，如果换成特征的话就是，某些特征起作用，而不是所有的特征起作用，这个去耦合的过程就是减小过拟合的过程），所以并不是只使用L1或者L2，有些时候会把L1和L2合起来用。而L2正则化是把w的绝对值变小了，而且考虑的特征要比L1多。并用代码实现了通过不同的λ来观察对结果的不同的影响，这次继续介绍解决过拟合的另外一种方法：丢弃法，并介绍前向传播和后向传播。

二：暂退法（dropout）

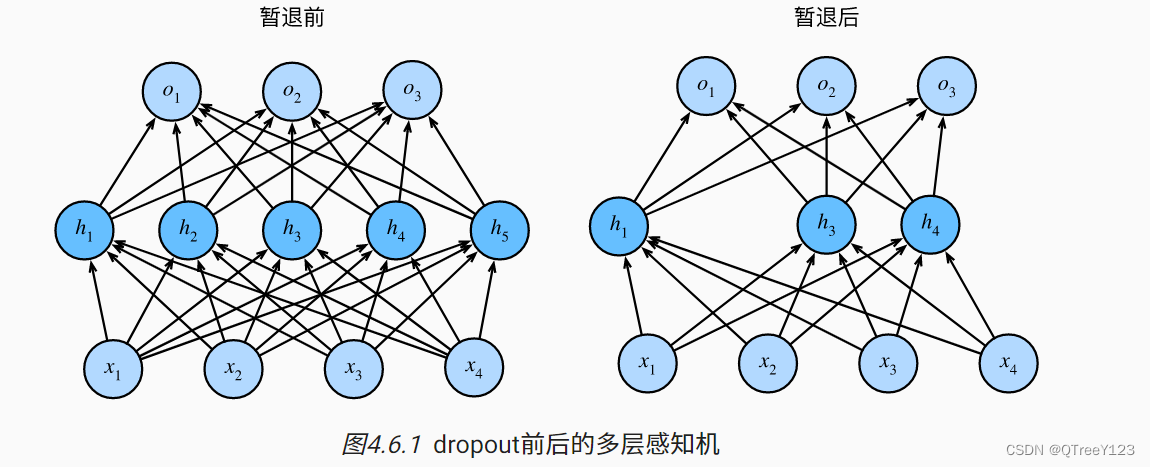
         暂退法在前向传播过程中，计算每一内部层的同时注入噪声，这已经成为训练神经网络的常用技术。 这种方法之所以被称为暂退法，因为我们从表面上看是在训练过程中丢弃（drop out）一些神经元。 在整个训练过程的每一次迭代中，标准暂退法包括在计算下一层之前将当前层中的一些节点置零。

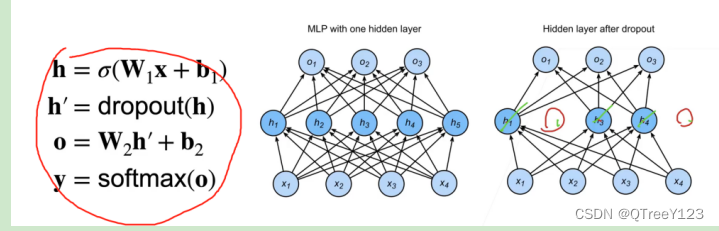
在标准暂退法正则化中，通过按保留（未丢弃）的节点的分数进行规范化来消除每一层的偏差。 换言之，每个中间活性值ℎ以暂退概率p由随机变量ℎ′替换，如下所示：

         丢弃法并没有改变每个神经元的期望输出值，只是随机地屏蔽一些神经元的输出。对于丢弃率为p的情况，我们可以将保留下来的神经元的输出值除以1-p来作为最终的输出。这样可以保证期望不变（期望仍是h），因为保留下来的神经元的输出值都被乘以了一个固定的因子1/(1-p)。因为对于离散型的数学期望，它的表达式是

根据此模型的设计，其期望值保持不变，即E[ℎ′]=ℎ,所以可以计算出期望不变（这里看了b站up主的讲解就理解了）

 三：实践中的暂退法

通常，我们在测试时不用暂退法。 给定一个训练好的模型和一个新的样本，我们不会丢弃任何节点，因此不需要标准化。 然而也有一些例外：一些研究人员在测试时使用暂退法， 用于估计神经网络预测的“不确定性”： 如果通过许多不同的暂退法遮盖后得到的预测结果都是一致的，那么我们可以说网络发挥更稳定。

通常将丢弃法作用在隐藏层全连接层的输出上 

 四：从零开始实现

要实现单层的暂退法函数， 我们从均匀分布U[0,1]中抽取样本，样本数与这层神经网络的维度一致。 然后我们保留那些对应样本大于p的节点，把剩下的丢弃。

import torch
from torch import nn
from d2l import torch as d2l

def dropout_layer(X, dropout):
    assert 0 <= dropout <= 1
    # 在本情况中，所有元素都被丢弃
    # dropout == 1：丢弃的概率是1
    if dropout == 1:
        return torch.zeros_like(X)
    # 在本情况中，所有元素都被保留
    if dropout == 0:
        return X
    #(torch.rand(X.shape) 0-1的均匀分布。将这个张量中每个元素与0.5比较，生成一个布尔型张量，即大于0.5的元素为 True(1)，小于等于0.5的元素为 False(0)
    mask = (torch.rand(X.shape) > dropout).float()
    #  mask(x的值) * x/(1-p) 
    return mask * X / (1.0 - dropout) 

num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
dropout1, dropout2 = 0.5, 0.5

我们可以通过下面几个例子来测试dropout_layer函数。 我们将输入X通过暂退法操作，暂退概率分别为0、0.5和1。

X= torch.arange(16, dtype = torch.float32).reshape((2, 8))
print(X)
print(dropout_layer(X, 0.))
print(dropout_layer(X, 0.5))
print(dropout_layer(X, 1.))
#tensor([[ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.],
#        [ 8.,  9., 10., 11., 12., 13., 14., 15.]])
#tensor([[ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.],
#        [ 8.,  9., 10., 11., 12., 13., 14., 15.]])
#tensor([[ 0.,  2.,  4.,  6.,  0.,  0.,  0., 14.],
#        [16., 18., 20., 22.,  0., 26.,  0., 30.]])
#tensor([[0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0.]])

定义模型参数定义模型

        我们可以将暂退法应用于每个隐藏层的输出（在激活函数之后）， 并且可以为每一层分别设置暂退概率： 常见的技巧是在靠近输入层的地方设置较低的暂退概率。 下面的模型将第一个和第二个隐藏层的暂退概率分别设置为0.2和0.5， 并且暂退法只在训练期间有效。

# 引入的Fashion-MNIST数据集。 我们定义具有两个隐藏层的多层感知机，每个隐藏层包含256个单元。
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
dropout1, dropout2 = 0.5, 0.5
class Net(nn.Module):
    def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,
                 is_training=True):
        super(Net, self).__init__()
        self.num_inputs = num_inputs
        # 只有在训练模型时才使用dropout
        self.training = is_training
        self.lin1 = nn.Linear(num_inputs, num_hiddens1)
        self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
        self.lin3 = nn.Linear(num_hiddens2, num_outputs)
        self.relu = nn.ReLU()

    def forward(self, X):
        H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))
        # 只有在训练模型时才使用dropout
        if self.training == True:
            # 在第一个全连接层之后添加一个dropout层
            H1 = dropout_layer(H1, dropout1)
        H2 = self.relu(self.lin2(H1))
        if self.training == True:
            # 在第二个全连接层之后添加一个dropout层
            H2 = dropout_layer(H2, dropout2)
        out = self.lin3(H2)
        return out

训练和测试

这类似于前面描述的多层感知机训练和测试。

# 引入的Fashion-MNIST数据集。 我们定义具有两个隐藏层的多层感知机，每个隐藏层包含256个单元。
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
dropout1, dropout2 = 0.5, 0.5
net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)

num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss()
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
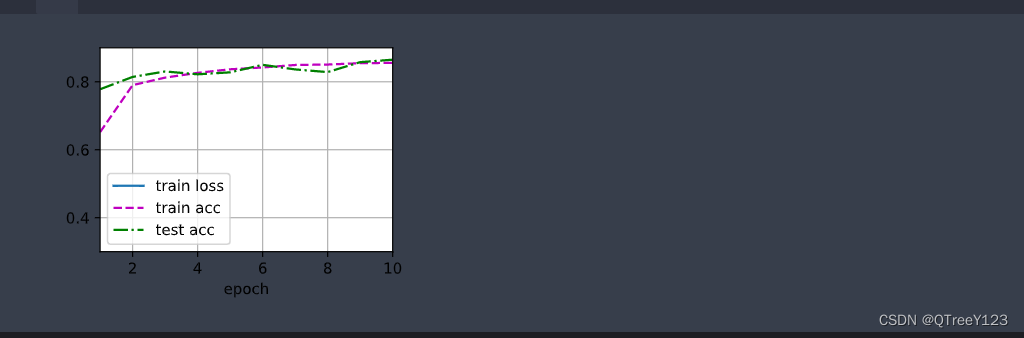
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
d2l.plt.show()

经过验证后，dropout和L2效果差不多，所以也当成正则化来使用

在dropout中，隐藏层的数据单元决定了你的训练效果好不好，因为要丢弃一些神经单元

 Tips：

        全连接层采用dropout，卷积层不需要dropout。对深度学习来讲，通常可以把模型弄得复杂点 ，然后通过正则化来控制模型复杂度， 就是有dropout的情况下，可以把隐藏层稍微设大一点点，再把dropout率也设大一点点 ，这样可能比不用dropout，而且隐藏层小一点点的效果会更好一点，Dropout是正则项，它的唯一作用是在更新权重的时候让你模型复杂度变低一点点。    

五：前向传播和后向传播

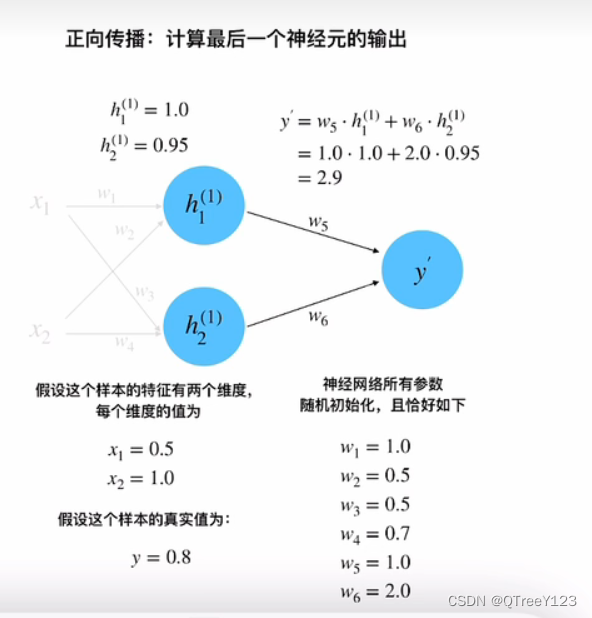
正向传播： 

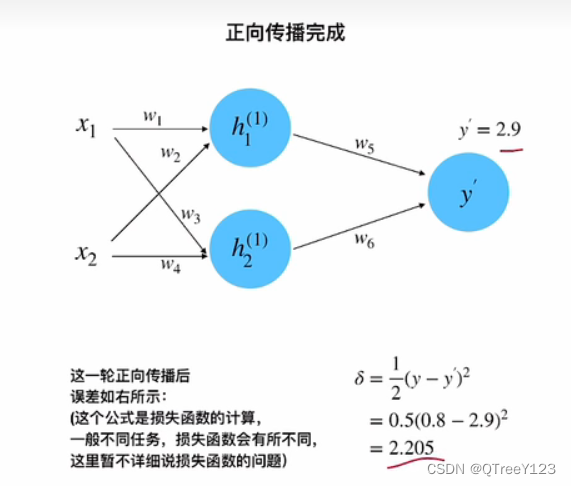
正向传播完成：

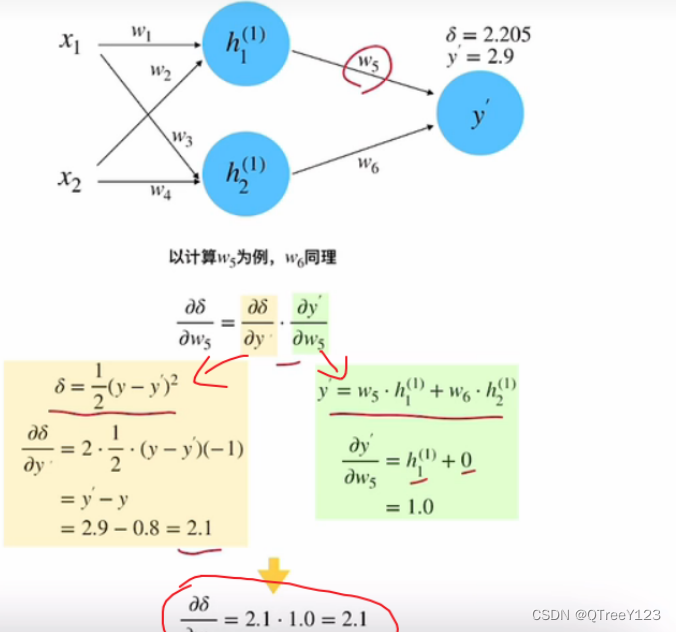
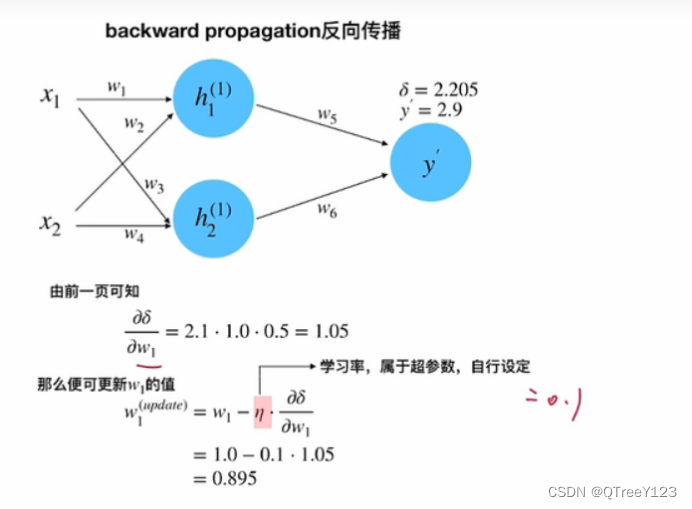
 反向传播

进行链式求导，先求出w5的梯度，更新w2值，再求出w1的梯度

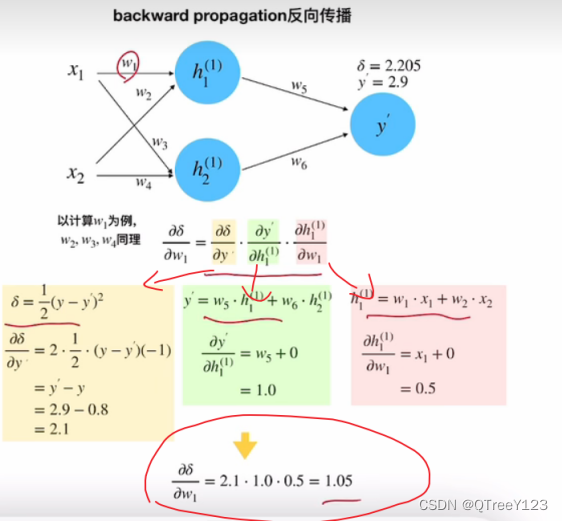
 继续反向传播w1

 更新w1的值

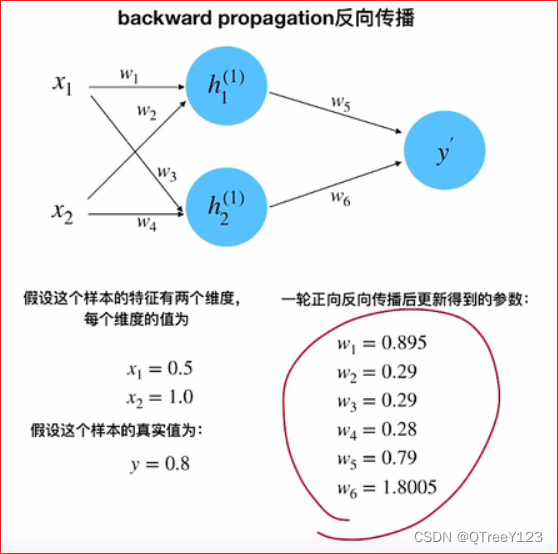
把所有的w都更新一遍，反向传播的一轮就结束了

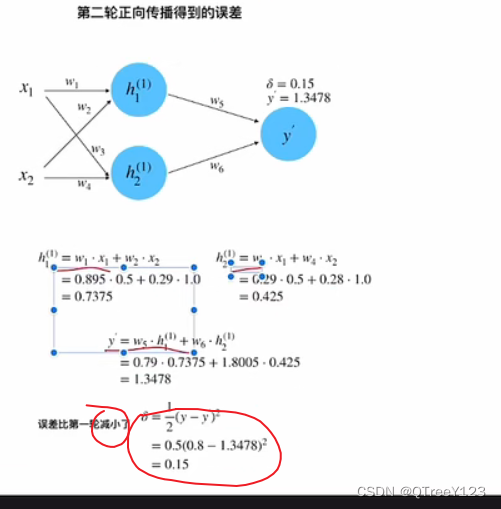
 下一轮又是从正向传播开始，损失比第一轮减小了0.15

事实上，正向传播的时候，除了对wx1+wx2…以外，还需要在括号乘以一个激活函数的，反向传播的时候也会对激活函数继续求导。

这个激活函数是relu，求导只有0和1，

相信大家看完这些图片后能对前向后向传播有更深刻的体会~ 

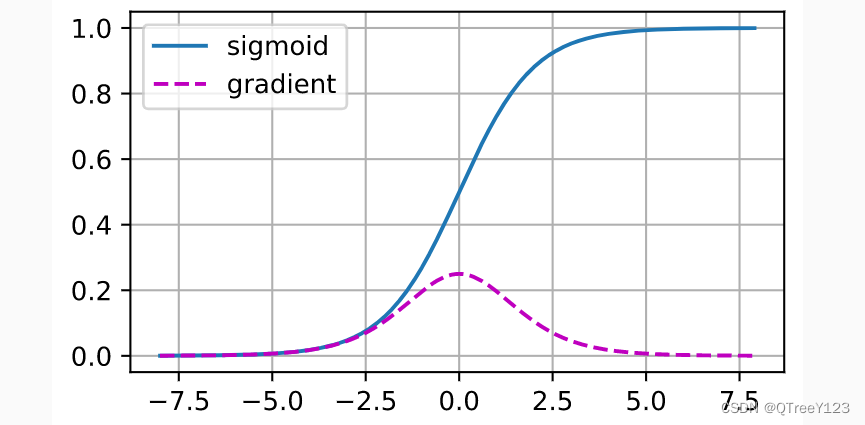
还有一小部分就是梯度消失和梯度爆炸，relu等激活函数可以减轻sigmoid带来的梯度消失和梯度爆炸，

         默认初始化方法通常是将参数随机初始化为小的随机值，例如从均匀分布或高斯分布中采样。这种方法在许多情况下效果很好，但是如果网络较深或输入特征数量较多，则会遇到梯度消失或梯度爆炸的问题。

        Xavier初始化使用从均匀分布或高斯分布中采样的随机数来初始化参数，并将其乘以一个标量，该标量取决于输入和输出的数量。这种方法可以减少梯度消失和梯度爆炸的问题，并提高模型的收敛速度和性能。Xavier初始化可以更好地处理较深的网络和大量的输入特征，但并不总是比默认初始化更好。实际中，这些方法通常会互相比较以获得最佳性能。

六：总结：

        本节介绍了dropout和前向后向传播的概念以及实现，下一篇我将分享一个线性回归模型实战项目——房价预测。

所有项目代码+UI界面

视频，笔记和代码,以及注释都已经上传网盘，放在主页置顶文章

今天的文章前向传播和反向传播的区别_神经网络dropout的概念分享到此就结束了，感谢您的阅读。