辗转相除法的原理_扩展欧几里得算法求逆元步骤

ps：全文图片均为手绘，如果有不标准的地方还望谅解，之后会慢慢熟悉画图工具的，感谢感谢！！！

1. 辗转相除

欧几里得算法又称为辗转相除法，是指用于计算两个非负整数a，b的最大公约数。

两个整数的最大公约数是指能够同时整除它们的最大的正整数。

辗转相除法能够实现效果主要基于以下原理：两个整数的最大公约数等于其中较小的数和两数相除余数的最大公约数。

原理用用公式表示为：gcd(a,b) = gcd(b,a mod b)。

其中gcd为最大公约数的英文greatest common divisor的缩写

mod相当于取模运算符%

最大公约数：两个或多个整数共有的最大公约数，用于表示这些整数之间的最大公共因子。

2. 辗转相除算法的几何描述

2.1 起源

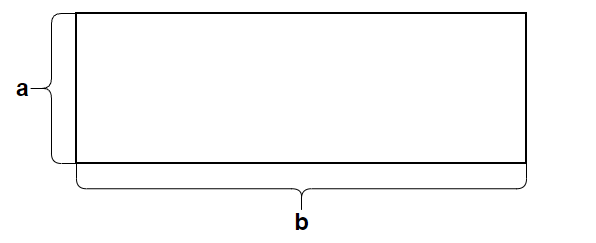
辗转相除算法起源于希腊，希腊人非常喜欢从图形或者用几何的角度去看待问题。希腊数学家甚至认为，所有的数字都与一个几何概念有关系。所以很自然地，希腊数学家在面对求两个数的最大公约数这个问题的时候，首先想到这个问题是否可以转换为一个几何问题来进行处理。在经过一些尝试之后。这一摄像得到实现：将所要求取最大公约数的两个数字a，b分别作为一个矩形的两条边，形成一个矩形。

前文提到，两个整数共有的最大公约数，就是用于表示这些整数之间公共因子中的最大的一个。这是一种偏于数学抽象化的描述。那么如何将其进行直观的表示出来呢？也就是如何将最大公约数问题从用数字表示，转化为几何图形的形式。

即：以需要求取最大公约数的两个数字为边长，构造出一个矩形。然后从这个矩形中寻找出一个小的矩形，或者说一个小的正方形，这个正方形可以没有缝隙的铺满上述构造出的矩形。明显的是这种正方形有很多个，这就像两个数字的公因子，可能存在很多个，而我们的任务就是找出其中最大的那个。

所以我们应该怎么找出这个最大的正方形呢？

2.2 铺瓷砖

不知道大家有没有看过装修的时候，工人师傅们铺瓷砖的场面。

我们是否可以把上述问题想象称为铺瓷砖，有一个长为a，宽为b的地面，需要铺满瓷砖，需要用多大的正方形瓷砖才能正好将其铺满。

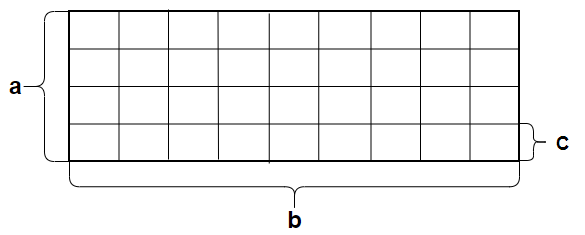
如果都用一样大小的正方形瓷砖，并且这个正方形为其可以选择的面积最大的正方形，那么铺瓷砖师傅的工作量将会大大减小吧。

如上图，所需正方形的变长c便是a和b的约数，即c为a和b的公约数，当c取到最大值时，即为a和b的最大公约数。

2.2.1 推导

为了解决上面的问题，我们可以先使用多种尺寸的正方形进行填补尝试，而我们的目的是找到允许存在的最大的正方形，那么我们先从最大面积开始尝试。

设宽为a，长为b，其中0<a<b

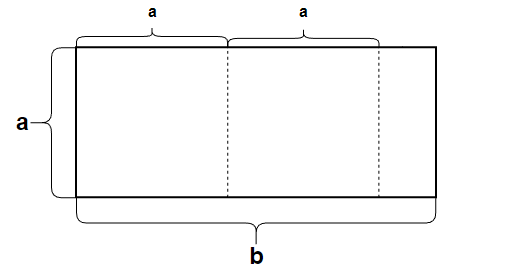
1. c取a，即正方形面积为a*a

   

   从左往右依次铺设变长为a的正方形，发现地面只能容纳两个，并且剩余一个矩形空间，显然不符合要求

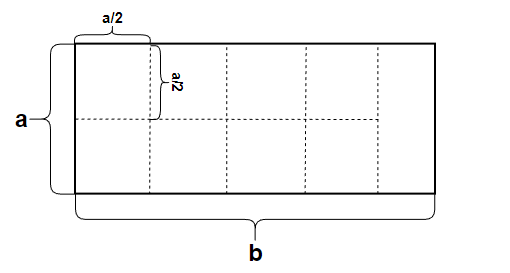
2. c取a/2，即正方形面积为a/2 * a/2

   

   从左往右依次铺设变长为a/2的正方形，发现地面只能容纳8个，并且剩余一个矩形空间，显然也不符合要求

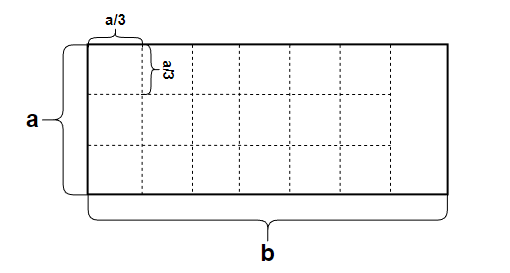
3. c取a/3，即正方形面积为a/3 * a/3

   

   从左往右依次铺设变长为a/3的正方形，发现地面只能容纳18个，并且剩余一个矩形空间，显然也不符合要求

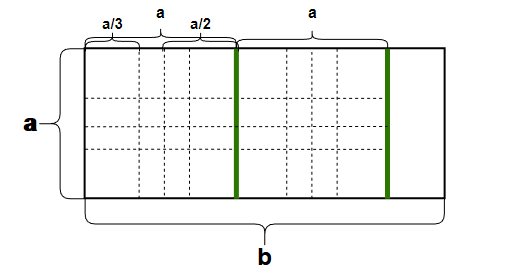
经过三次尝试，我们发现总是不能满足我们的要求，并且每一次右边都会剩余一部分矩形，对比三张图片发现，它们剩余的矩形区域似乎差不多大小，这是一个新奇的发现，是否真的如同我们所想，剩余区域其实是相同大小的矩形呢？我们尝试着把三个图形进行重叠

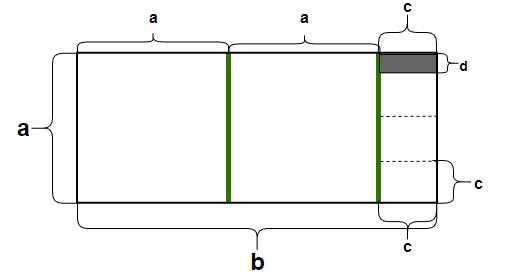
上图为将前三图重合之后得到，此时我们发现三个图不同大小的正方形进行填充会存在边重合的现象，并且每次填充剩余矩形的大小的确为相同的面积。虚线重合地方为绿色加粗线条。

也就是说，无论是使用哪一种大小的正方形进行填充，我们都会先把前面绿线前面的以短边a为面积构成的正方形填充掉，剩余一个矩形，那么我们是否可以这样想？

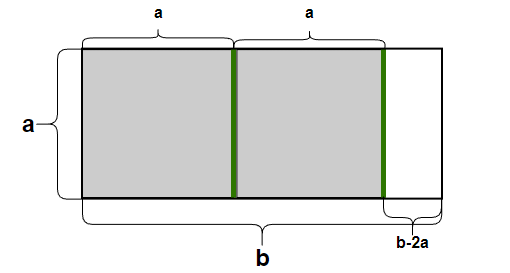
把以a为边长的正方形填充的区域，直接当做已经填充的区域，从绿线之后的区域开始填充。那么此时这个问题就变成了：如何用面积相同的正方形填满长为a，宽为b-a的长方形呢。此时我们相当于简化了原先的问题。

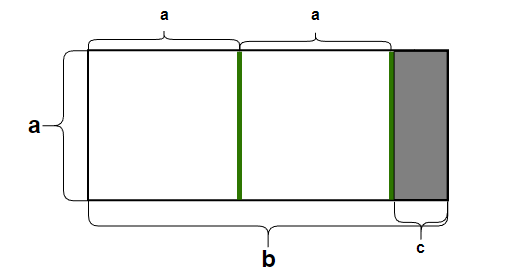
去除两个灰色的面积为a*a的正方形，我们得到了一个细长竖直的长方形，此时短边为(b-a)，长边为a

用长边b / 短边a 得到的余数即为c

此时我们设：c = b%a，即：

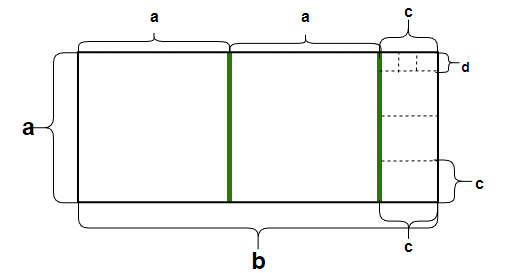
此时短边为c，长边为a，我们重复上面的流程，用c为边长的正方形填充灰色区域，然后在去掉填充区域，得到短边为d，长边为c的长方形区域。

用长边a / 短边c 得到的余数即为d

此时设：d = a%c

此时短边为d，长边为c。再次重复上述流程，用d为边长的正方形填充灰色区域。

用长边c / 短边d 得到的余数为0

此时 c%d ==0 即代表不在存在未填充区域

我们发现，面积为d*d的正方形正好填充满这个长方形。

综上所述，用面积为 d*d 的正方形恰好可以填满最初面积为 a*b的长方形，这种方式就是辗转相除法

3. 最大公约数

现在，我们可以尝试使用辗转相除法，也就是上面贴瓷砖的逻辑，来试求最大公因数。

例如：我们设两个数，a=6,b=16，求两个数的最大公约数

其中较小者为a，我们用b%a（16%6），得到c=4

此时长边为6，短边为4，再用a%c（6%4），得到d=2

此时长边为4，短边为2，再用c%2（4%2），得到 0

如此：在最后一步实现了整除，此时除数也就是短边为 2 ，这就是6和16的最大公约数

回顾上述过程，我们发现其流程与C语言中的函数，递归非常相似，那么我们是否可将其抽象为一个函数呢？

最大公约数的英文为：greatest common divisor 取简称为gcd

设函数名为 gcd，函数参数为需要求最大公约数的两个整数，得出 gcd（a,b）；

再次回顾流程，发现每一次不是用长边去除短边，我们可以将每次得到的长边再次赋值给a，短边赋值给b，虽然这与前文不同，但是更符合我们的习惯。长在前，短在后

3.1 算法实现

#include<stdio.h>

int Gcd(int a, int b)
{ 
   
	if (b == 0)
	{ 
   
		return a;
	}
	else
	{ 
   
		return Gcd(b, a % b);
	}
}

int main()
{ 
   
	int a = 0;
	int b = 0;
	int ret = 0;
	scanf("%d %d", &a, &b);

	ret = Gcd(a, b);

	printf("%d和%d的最大公约数是：%d\n", a, b, ret);
	return 0;
}

ps：很久都没有写过博客了，有些地方讲述可能会有些问题，或者模糊。如果有问题，麻烦各位提出，非常感谢。

引用：
辗转相除法介绍
欧几里得算法

今天的文章辗转相除法的原理_扩展欧几里得算法求逆元步骤分享到此就结束了，感谢您的阅读。