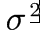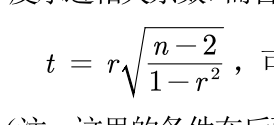相关系数表明两个变量之间的什么关系_相关系数如何判断相关性

目录

1.皮尔逊Pearson相关系数

1）总体

2）样本

3）易错

4）画散点图

5）判断相关性大小​

6 )描述性统计

 7）美化（相关性可视化）

2.对皮尔逊相关系数进行假设检验

1）构造统计变量

2）假设检验部分

 3.正态性检验

 1）JB检验（大样本 n>30） 

2）小样本3≤n≤50：Shapiro-wilk检验

 3）QQ图

4.斯皮尔曼相关系数

1）相关系数定义

2）假设检验

1.皮尔逊Pearson相关系数

先描述性统计，正态性检验，皮尔逊相关系数，显著性

1）总体

2）样本

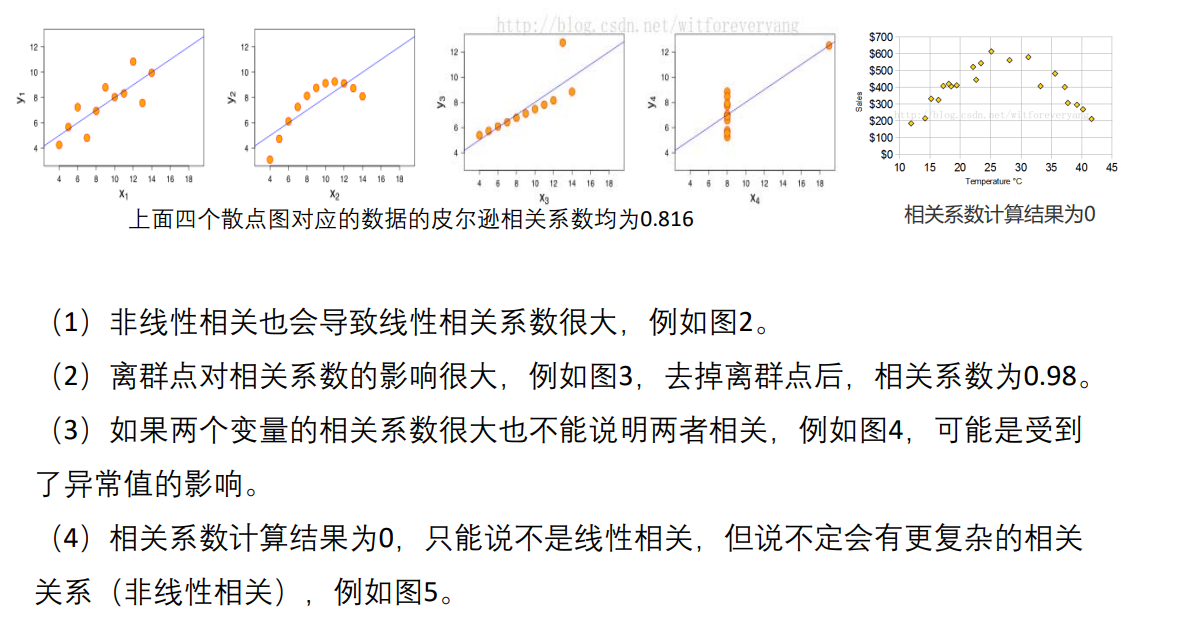
3）易错

4）画散点图

所以先画散点图（用spss）再观察是否有线性关系，有的话用皮尔逊，否则不能用 

这里使用Spss比较方便: 图形 – 旧对话框 – 散点图/点图 – 矩阵散点图

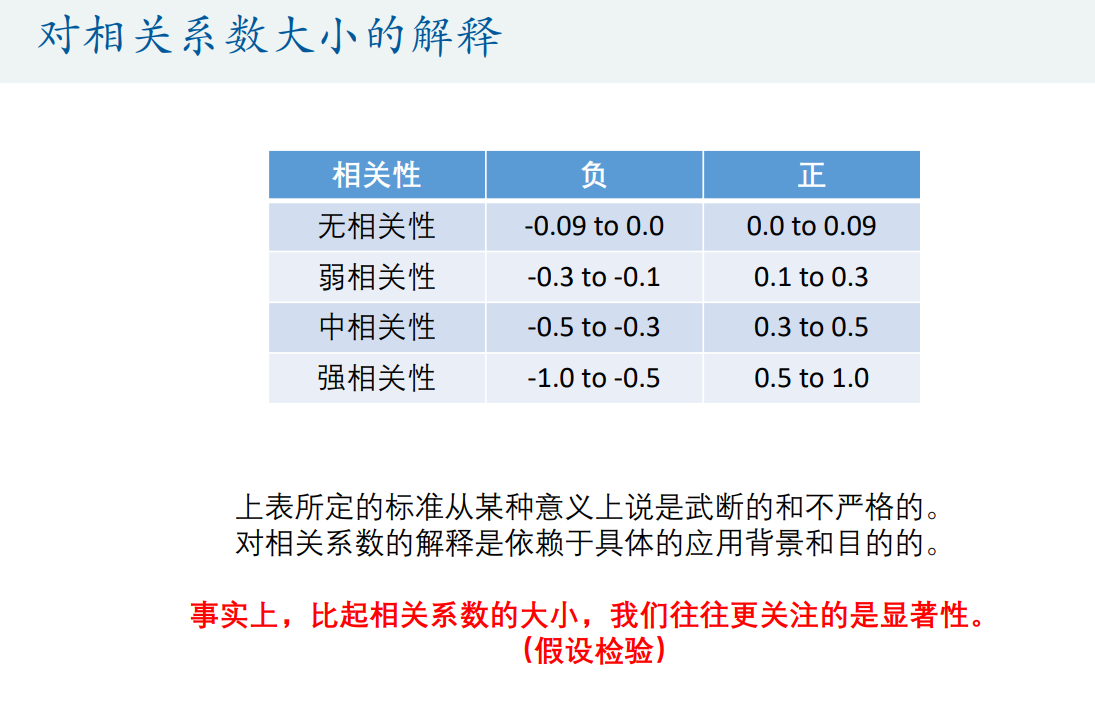
5）判断相关性大小

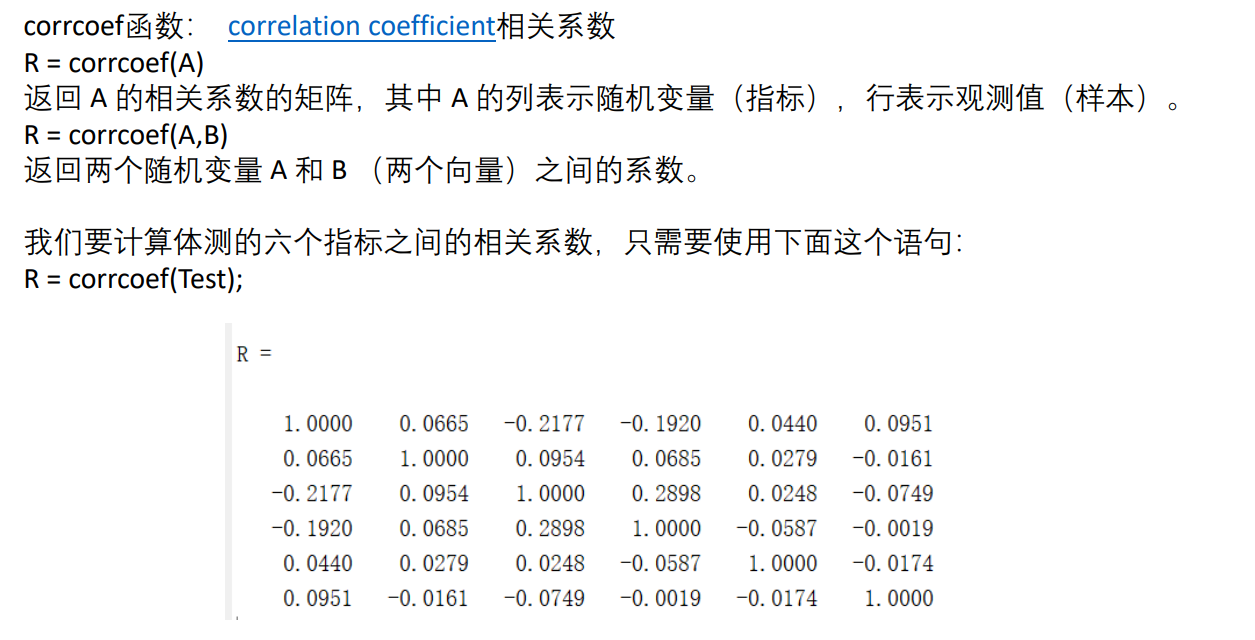
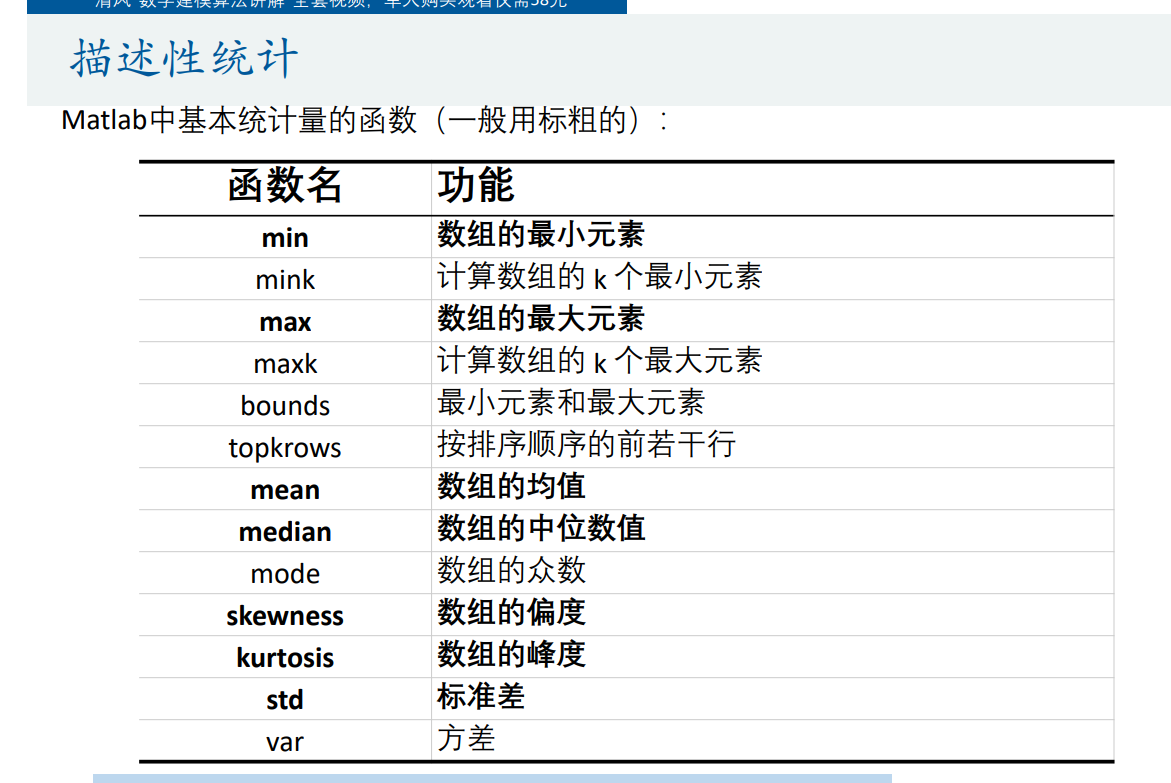
R = corrcoef(Test)   % correlation coefficient

6 )描述性统计

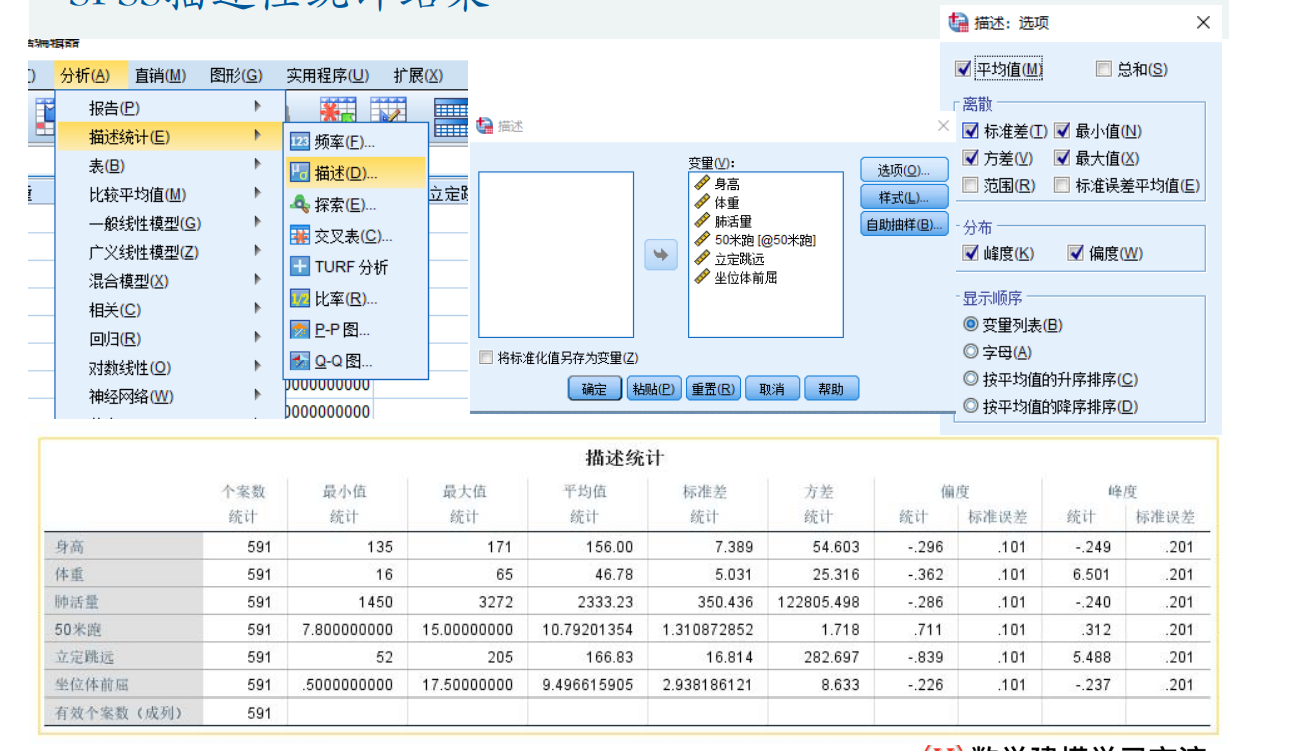
用SPSS和excel都可以

方法：

excel：数据分析->描述统计->汇总统计

spss：

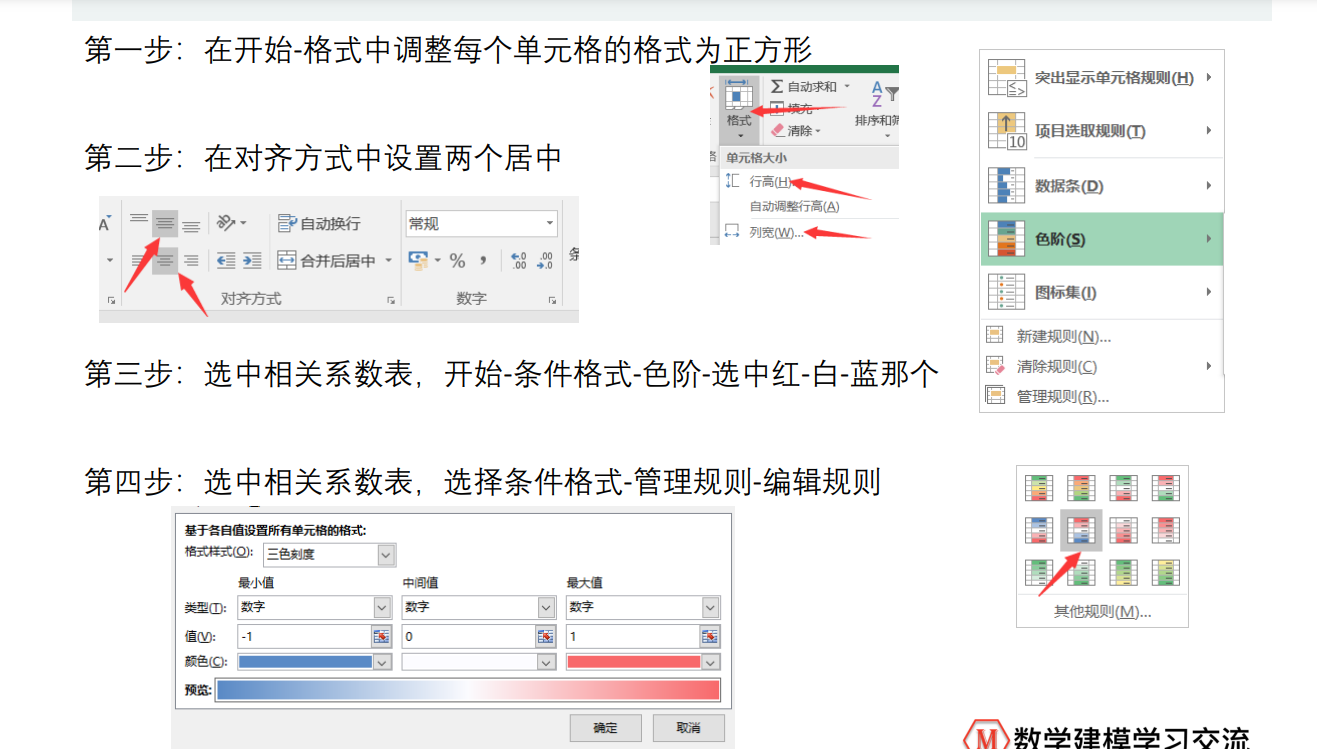
MIN = min(Test);  % 每一列的最小值MAX = max(Test);   % 每一列的最大值MEAN = mean(Test);  % 每一列的均值MEDIAN = median(Test);  %每一列的中位数SKEWNESS = skewness(Test); %每一列的偏度KURTOSIS = kurtosis(Test);  %每一列的峰度STD = std(Test);  % 每一列的标准差RESULT = [MIN;MAX;MEAN;MEDIAN;SKEWNESS;KURTOSIS;STD]  %将这些统计量放到一个矩阵中表示

 7）美化（相关性可视化）

2.对皮尔逊相关系数进行假设检验

1）构造统计变量

n-2是自由度，n为样本数量，r皮尔逊相关系数（corroef）

n趋近于无穷时，为标准正态分布

 ->算出对应检测值t

补正态分布

为X~N（u，），u=0，

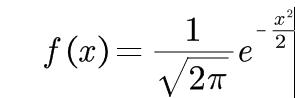
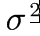
=1 

2）假设检验部分

<1>*画直线的技巧

tpdf（x，n）概率密度函数，x为横坐标范围，n为自由度

tcdf（t，n）累积概率密度函数，t检测值，n自由度

tinv（l，n）tcdf的反函数，l：概率，就是正态分布图像面积，从负无穷到所求临界值之间的面积，n为自由度

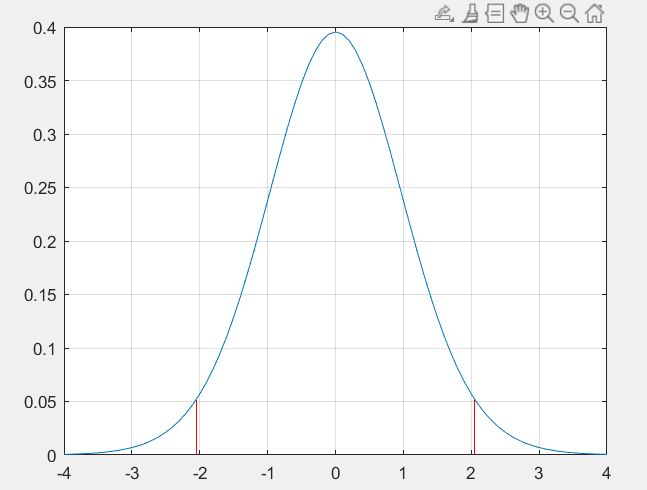
x = -4:0.1:4;y = tpdf(x,28);  %求t分布的概率密度值 28是自由度  figure(1)plot(x,y,'-')grid on  % 在画出的图上加上网格线hold on  % 保留原来的图，以便继续在上面操作% matlab可以求出临界值，函数如下tinv(0.975,28)    %    2.0484% 这个函数是累积密度函数cdf的反函数plot([-2.048,-2.048],[0,tpdf(-2.048,28)],'r-')plot([2.048,2.048],[0,tpdf(2.048,28)],'r-')

补充： “如果呈现出显著性（结果右上角有*号，此时说明有关系；反之则没有关系）；有了关系之后，关系的紧密程度直接看相关系数大小即可。一般0.7以上说明关系非常紧密；0.4~0.7之间说明关系紧密；0.2~0.4说明关系一般.”转载

总结：有假设才有显著性,先看显著性,之后观察相关性的紧密程度

<2> 另一种方法：

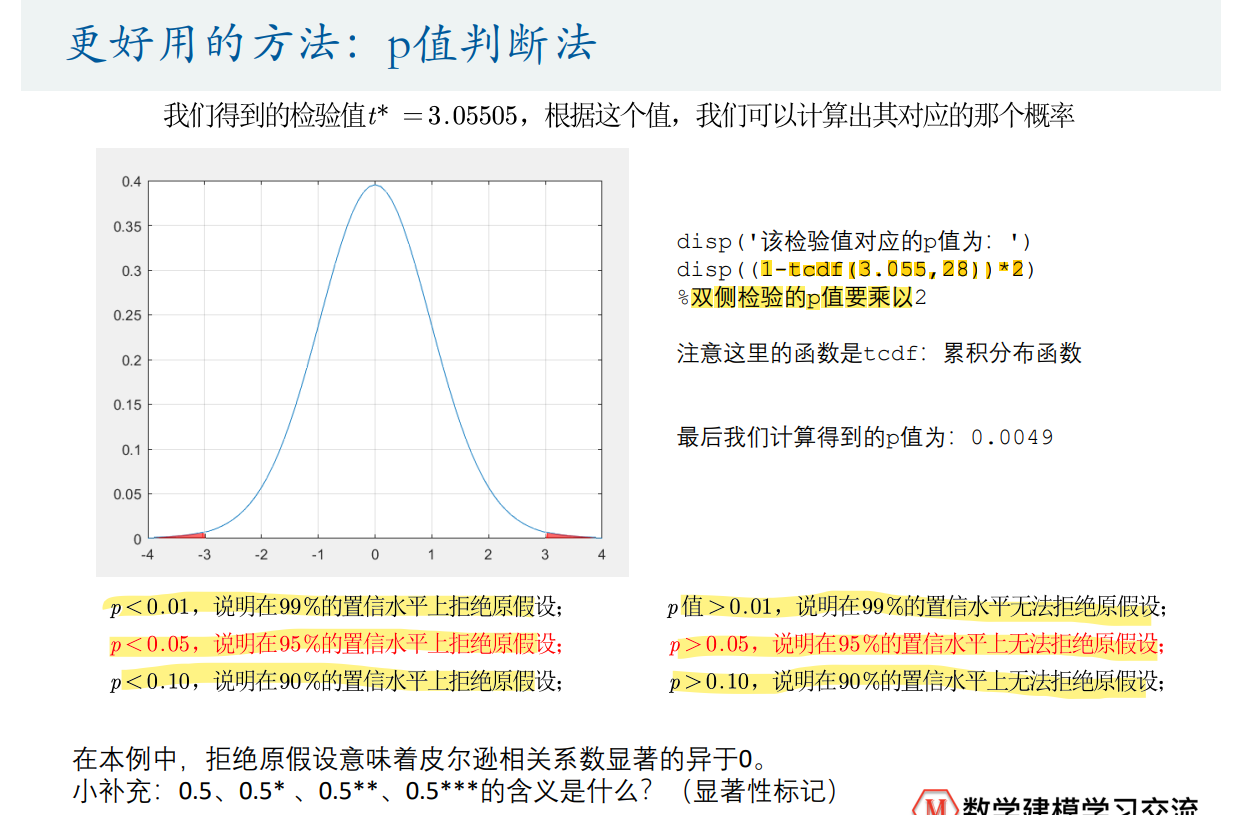
p值判断法

单侧检验：p=(1-tcdf(t,n))

双侧检验*2：p=(1-tcdf(t,n))*2

 0.5：无显著性，无法拒绝原假设

0.5*：在90%置信上拒绝原假设

0.5**：在95%置信上拒绝原假设

0.5***：在99%置信上拒绝原假设

计算单个p值：

x = -4:0.1:4;y = tpdf(x,28);figure(2)plot(x,y,'-')grid on hold on% 画线段的方法plot([-3.055,-3.055],[0,tpdf(-3.055,28)],'r-')plot([3.055,3.055],[0,tpdf(3.055,28)],'r-')disp('该检验值对应的p值为：')disp((1-tcdf(3.055,28))*2)  %双侧检验的p值要乘以2

计算各列之间的相关系数以及p值： 之后在excel中标记星号

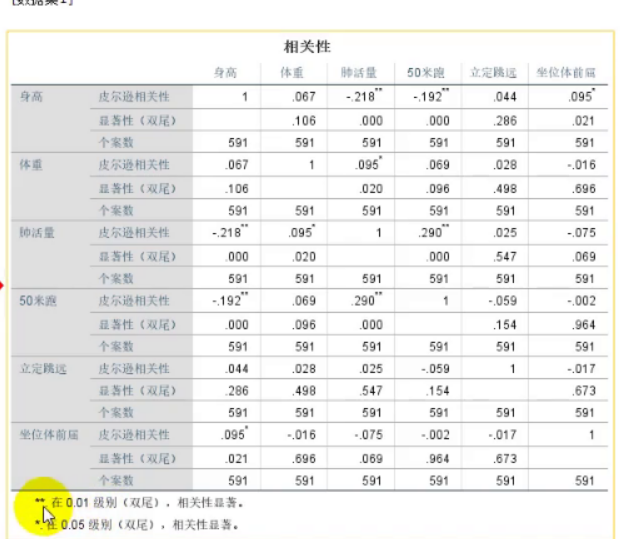
[R,P] = corrcoef(Test)% 在EXCEL表格中给数据右上角标上显著性符号吧P < 0.01  % 标记3颗星的位置(P < 0.05) .* (P > 0.01)  % 标记2颗星的位置(P < 0.1) .* (P > 0.05) % % 标记1颗星的位置

标记*也可用SPSS：分析->相关->双变量

但标注*的规则不同

 3.正态性检验

原因：计算是皮尔逊相关系数的前提

 1）JB检验（大样本 n>30） 

雅克‐贝拉检验

函数jbtest（x，alpha）：x，检测的向量（不能是矩阵）， alpha，显著性水平0.05，此刻的置信水平0.95

h=1，拒绝原假设，h=0不能拒绝原假设

h，p都为一个值

<1>检测一组数据是否满足正态性

[h,p] = jbtest(Test(:,1),0.05)[h,p] = jbtest(Test(:,1),0.01)

 <2>用循环检验所有列

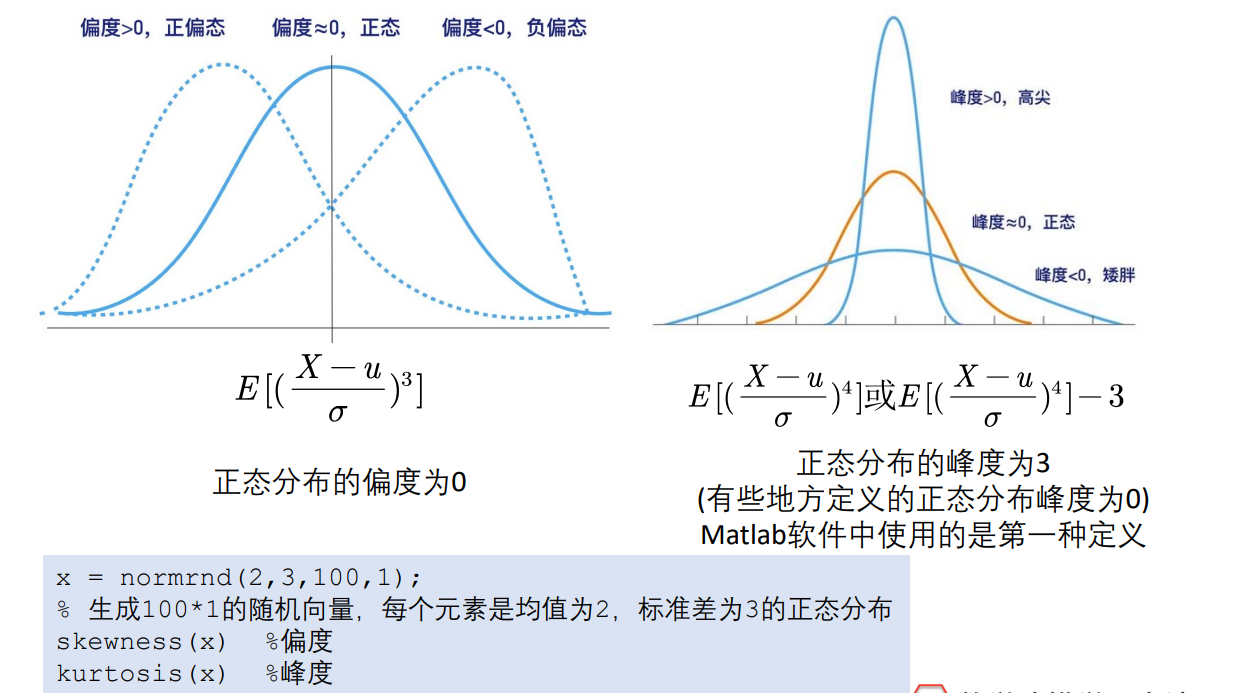
n_c = size(Test,2);  % number of column 数据的列数H = zeros(1,6);  % 初始化节省时间和消耗P = zeros(1,6);for i = 1:n_c    [h,p] = jbtest(Test(:,i),0.05);    H(i)=h;    P(i)=p;enddisp(H)disp(P)

补：偏度峰度

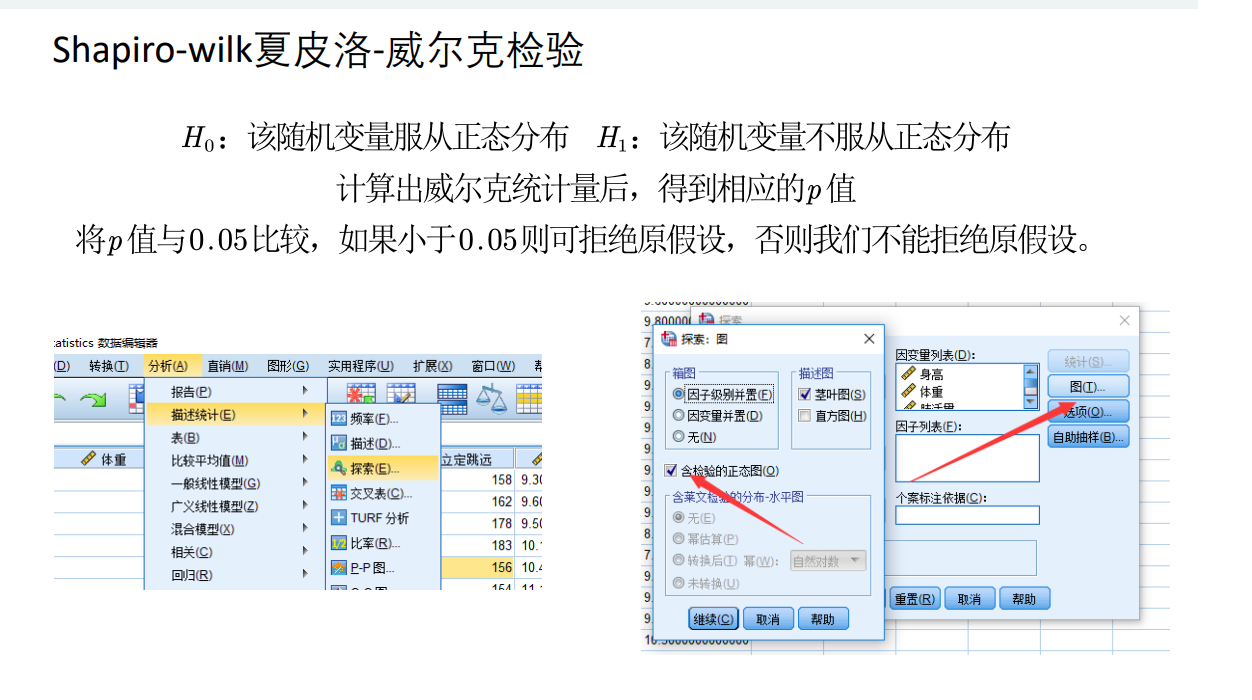
% 正态分布的偏度和峰度x = normrnd(2,3,100,1);   % 生成100*1的随机向量，每个元素是均值为2，标准差为3的正态分布skewness(x)  %偏度kurtosis(x)  %峰度qqplot(x)

2）小样本3≤n≤50：Shapiro-wilk检验

只能用spss

 3）QQ图

Q‐Q图鉴别样本数据是否近似于正态分布,只需看Q‐Q图上的点 是否近似地在一条直线附近。（要求数据量非常大）

qqplot(Test(:,1))

4.斯皮尔曼相关系数

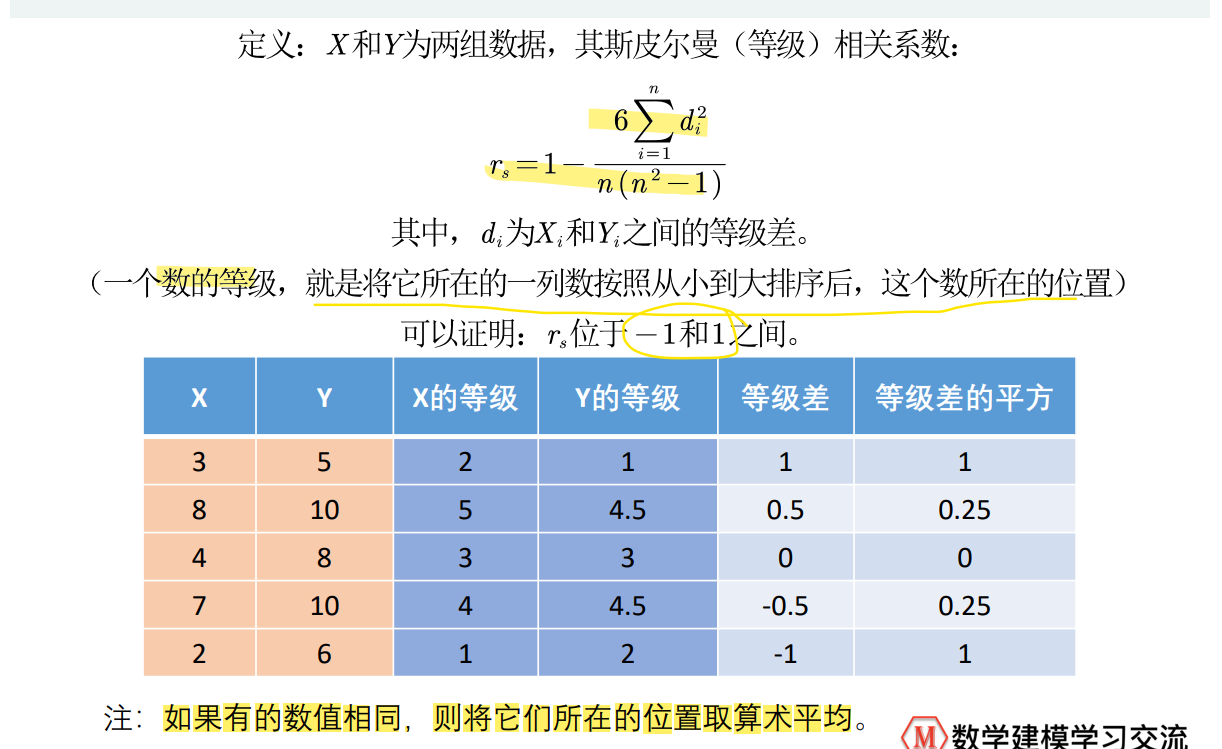
1）相关系数定义

XY必须是列向量

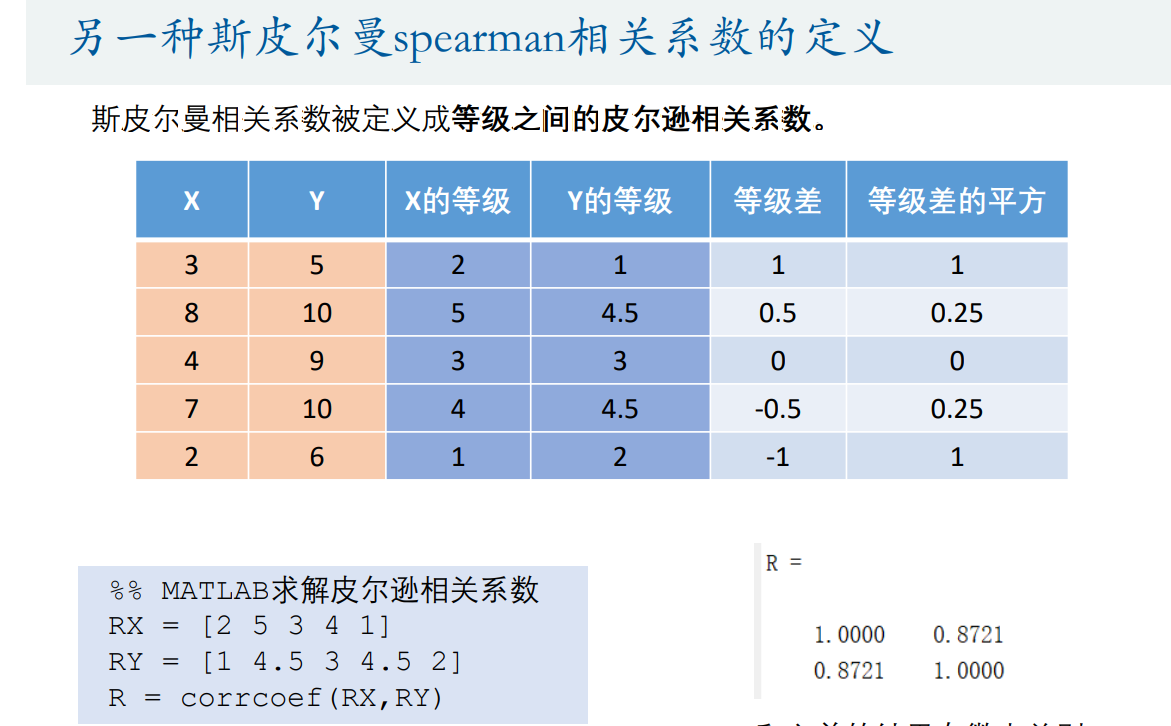
 Matlab使用的是第二种计算方法

%% 斯皮尔曼相关系数X = [3 8 4 7 2]'  % 一定要是列向量哦，一撇'表示求转置Y = [5 10 9 10 6]'% 第一种计算方法1-6*(1+0.25+0.25+1)/5/24% 第二种计算方法coeff = corr(X , Y , 'type' , 'Spearman')% 等价于：RX = [2 5 3 4 1]RY = [1 4.5 3 4.5 2]R = corrcoef(RX,RY)% 计算矩阵各列的斯皮尔曼相关系数R = corr(Test, 'type' , 'Spearman')

2）假设检验

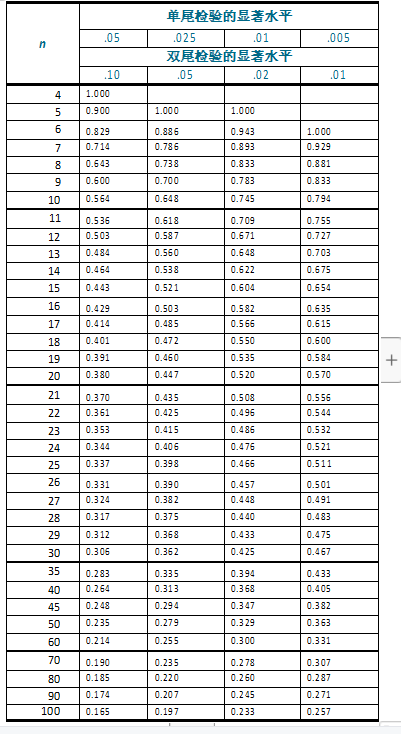
小样本

大样本

计算检测值t:

计算p值:

双侧p=(1-normcdf(t))*2

单侧p=1-normcdf(t)

% 计算检验值disp(sqrt(590)*0.0301)% 计算p值disp((1-normcdf(0.7311))*2) % normcdf用来计算标准正态分布的累积概率密度函数% 直接给出相关系数和p值[R,P]=corr(Test, 'type' , 'Spearman')

定序必须要用斯皮尔曼相关系数 

今天的文章相关系数表明两个变量之间的什么关系_相关系数如何判断相关性分享到此就结束了，感谢您的阅读。